estimate

Оцените апостериорное распределение Байесовых параметров модели линейной регрессии

Синтаксис

PosteriorMdl = estimate(PriorMdl,X,y)

PosteriorMdl = estimate(PriorMdl,X,y,Name,Value)

[PosteriorMdl,Summary]
= estimate(___)

Описание

Чтобы выполнить выбор переменного предиктора для Байесовой модели линейной регрессии, смотрите estimate.

пример

PosteriorMdl = estimate(PriorMdl,X,y) возвращает Байесовую модель PosteriorMdl линейной регрессии это характеризует объединенные апостериорные распределения коэффициентов β и отклонение воздействия σ ². PriorMdl задает объединенное предшествующее распределение параметров и структуру модели линейной регрессии. X данные о предикторе и y данные об ответе. PriorMdl и PosteriorMdl не может быть тот же тип объекта.

Произвести PosteriorMdl, estimate функционируйте обновляет предшествующее распределение с информацией о параметрах, которые это получает из данных.

NaNs в данных указывают на отсутствующие значения, который estimate удаляет при помощи мудрого списком удаления.

пример

PosteriorMdl = estimate(PriorMdl,X,y,Name,Value) задает дополнительные опции с помощью одного или нескольких аргументов пары "имя-значение". Например, можно задать значение или для β или для σ ², чтобы оценить апостериорное распределение conditional одного параметра, учитывая заданное значение другого параметра.

Если вы задаете Beta или Sigma2 аргумент пары "имя-значение", затем PosteriorMdl и PriorMdl равны.

пример

[PosteriorMdl,Summary] = estimate(___) использование любая из комбинаций входных аргументов в предыдущих синтаксисах, чтобы возвратить таблицу, которая содержит следующее для каждого параметра: следующее среднее и стандартное отклонение, 95%-й вероятный интервал, апостериорная вероятность, что параметр больше 0, и описание апостериорного распределения (если вы существуете). Кроме того, таблица содержит следующую ковариационную матрицу β и σ ². Если вы задаете Beta или Sigma2 аргумент пары "имя-значение", затем estimate возвращает условные следующие оценки.

Примеры

свернуть все

Сравните предшествующую и крайнюю следующую оценку по умолчанию оценками OLS

Скрипт Open Live Script

Рассмотрите модель, которая предсказывает экономию топлива (в MPG) автомобиля, учитывая его объем двигателя и вес.

Загрузите carsmall набор данных.

load carsmall
x = [Displacement Weight];
y = MPG;

Экономия топлива регресса на объем двигателя и вес, включая точку пересечения, чтобы получить оценки обычных наименьших квадратов (OLS).

Mdl = fitlm(x,y)

Mdl = 
Linear regression model:
    y ~ 1 + x1 + x2

Estimated Coefficients:
                    Estimate        SE         tStat       pValue  
                   __________    _________    _______    __________

    (Intercept)        46.925       2.0858     22.497    6.0509e-39
    x1              -0.014593    0.0082695    -1.7647      0.080968
    x2             -0.0068422    0.0011337    -6.0353    3.3838e-08


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 4.09
R-squared: 0.747,  Adjusted R-Squared: 0.741
F-statistic vs. constant model: 134, p-value = 7.22e-28

Mdl.MSE

ans = 16.7100

Создайте значение по умолчанию, рассейте предшествующее распределение для одного предиктора.

p = 2;
PriorMdl = bayeslm(p);

PriorMdl diffuseblm объект модели.

Используйте опции по умолчанию, чтобы оценить апостериорное распределение.

PosteriorMdl = estimate(PriorMdl,x,y);

Method: Analytic posterior distributions
Number of observations: 94
Number of predictors:   3
 
           |   Mean     Std         CI95        Positive       Distribution     
--------------------------------------------------------------------------------
 Intercept | 46.9247  2.1091  [42.782, 51.068]    1.000   t (46.92, 2.09^2, 91) 
 Beta(1)   | -0.0146  0.0084  [-0.031,  0.002]    0.040   t (-0.01, 0.01^2, 91) 
 Beta(2)   | -0.0068  0.0011  [-0.009, -0.005]    0.000   t (-0.01, 0.00^2, 91) 
 Sigma2    | 17.0855  2.5905  [12.748, 22.866]    1.000   IG(45.50, 0.0013)

PosteriorMdl conjugateblm объект модели.

Следующие средние значения и содействующие оценки OLS почти идентичны. Кроме того, следующие стандартные отклонения и стандартные погрешности OLS почти идентичны. Следующее среднее значение Sigma2 близко к среднеквадратической ошибке (MSE) OLS.

Оцените следующий Используя гамильтонов сэмплер Монте-Карло

Открыть скрипт

Рассмотрите модель многофакторной линейной регрессии, которая предсказывает США действительный валовой национальный продукт (GNPR) использование линейной комбинации общей занятости (E) и действительная заработная плата (WR).

$\texttt{GNPR}_t=\beta_0+\beta_2\texttt{E}_t+\beta_3\texttt{WR}_t+\varepsilon_t.$

Для всех $t$ , $\varepsilon_t$ серия независимых Гауссовых воздействий со средним значением 0 и отклонение $\sigma^2$ . Примите эти предшествующие распределения:

$\beta_j\vert\sigma^2$ 3-D t распределение с 10 степенями свободы для каждого компонента, корреляционная матрица C, местоположение ct, и масштабируйте st.
$\sigma^2 \sim IG(r_1,r_2)$ , с формой и шкалой.

bayeslm обработки эти предположения и вероятность данных, как будто следующее соответствие аналитически тяжело.

Объявите функцию MATLAB® что:

Принимает значения $\beta$ и $\sigma^2$ вместе в вектор-столбце и принимает значения гиперпараметров
Возвращает значение объединенного предшествующего распределения $\pi\left(\beta,\sigma^2\right)$ , учитывая значения $\beta$ и $\sigma^2$

function logPDF = priorMVTIG(params,ct,st,dof,C,a,b)
%priorMVTIG Log density of multivariate t times inverse gamma 
%   priorMVTIG passes params(1:end-1) to the multivariate t density
%   function with dof degrees of freedom for each component and positive
%   definite correlation matrix C. priorMVTIG returns the log of the product of
%   the two evaluated densities.
%   
%   params: Parameter values at which the densities are evaluated, an
%           m-by-1 numeric vector.
%
%       ct: Multivariate t distribution component centers, an (m-1)-by-1
%           numeric vector.  Elements correspond to the first m-1 elements
%           of params.
%
%       st: Multivariate t distribution component scales, an (m-1)-by-1
%           numeric (m-1)-by-1 numeric vector.  Elements correspond to the
%           first m-1 elements of params.
%
%      dof: Degrees of freedom for the multivariate t distribution, a
%           numeric scalar or (m-1)-by-1 numeric vector. priorMVTIG expands
%           scalars such that dof = dof*ones(m-1,1). Elements of dof
%           correspond to the elements of params(1:end-1).
%
%        C: Correlation matrix for the multivariate t distribution, an
%           (m-1)-by-(m-1) symmetric, positive definite matrix. Rows and
%           columns correspond to the elements of params(1:end-1).
% 
%        a: Inverse gamma shape parameter, a positive numeric scalar.
%
%        b: Inverse gamma scale parameter, a positive scalar.
%
beta = params(1:(end-1));
sigma2 = params(end);

tVal = (beta - ct)./st;
mvtDensity = mvtpdf(tVal,C,dof);
igDensity = sigma2^(-a-1)*exp(-1/(sigma2*b))/(gamma(a)*b^a);

logPDF = log(mvtDensity*igDensity);
end

Создайте анонимную функцию, которая действует как priorMVTIG, но принимает значения параметров только и содержит гиперзначения параметров, зафиксированные в произвольно выбранных значениях.

prednames = ["E" "WR"];
p = numel(prednames);
numcoeff = p + 1;

rng(1); % For reproducibility
dof = 10;
V = rand(numcoeff);
Sigma = 0.5*(V + V') + numcoeff*eye(numcoeff);
st = sqrt(diag(Sigma));
C = diag(1./st)*Sigma*diag(1./st);
ct = rand(numcoeff,1);
a = 10*rand;
b = 10*rand;
logPDF = @(params)priorMVTIG(params,ct,st,dof,C,a,b);

Создайте пользовательскую объединенную предшествующую модель для параметров линейной регрессии. Задайте количество предикторов p. Кроме того, задайте указатель на функцию для priorMVTIG и имена переменных.

PriorMdl = bayeslm(p,'ModelType','custom','LogPDF',logPDF,...
    'VarNames',prednames);

PriorMdl customblm Байесов объект модели линейной регрессии, представляющий предшествующее распределение коэффициентов регрессии и отклонения воздействия.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда предиктора и ответа.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,"GNPR"};

Оцените крайние апостериорные распределения $\beta$ и $\sigma^2$ использование сэмплера Гамильтонова Монте-Карло (HMC). Задайте выборки рисунка 10,000, и электротермотренировка 1 000 чертит.

PosteriorMdl = estimate(PriorMdl,X,y,'Sampler','hmc','NumDraws',1e4,...
    'Burnin',1e3);

Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors:   3
 
           |    Mean       Std            CI95         Positive  Distribution 
------------------------------------------------------------------------------
 Intercept |   -3.6486    5.6293  [-16.215,  6.143]      0.246     Empirical  
 E         |   -0.0056    0.0006   [-0.007, -0.004]      0.000     Empirical  
 WR        |   15.2464    0.7727   [13.722, 16.749]      1.000     Empirical  
 Sigma2    | 1287.5830  243.1634  [894.978, 1849.210]    1.000     Empirical

PosteriorMdl empiricalblm объект модели, хранящий ничьи от апостериорных распределений.

Просмотрите график трассировки и график ACF ничьих от следующего из $\beta_1$ (например), и отклонение воздействия. Не стройте электротермотренировку.

figure;
subplot(2,1,1)
plot(PosteriorMdl.BetaDraws(2,1001:end));
title(['Trace Plot ' char(8212) ' \beta_1']);
xlabel('MCMC Draw')
ylabel('Simulation Index')
subplot(2,1,2)
autocorr(PosteriorMdl.BetaDraws(2,1001:end))

figure;
subplot(2,1,1)
plot(PosteriorMdl.Sigma2Draws(1001:end));
title(['Trace Plot ' char(8212) ' Disturbance Variance']);
xlabel('MCMC Draw')
ylabel('Simulation Index')
subplot(2,1,2)
autocorr(PosteriorMdl.Sigma2Draws(1001:end))

Выборка MCMC отклонения воздействия, кажется, смешивается хорошо.

Оцените условные апостериорные распределения

Скрипт Open Live Script

Считайте модель регрессии в Оценке Следующей Используя гамильтонов Сэмплер Монте-Карло. Этот пример использует те же данные и контекст, но принимает рассеянную предшествующую модель вместо этого.

Создайте рассеянную предшествующую модель для параметров линейной регрессии. Задайте количество предикторов p и имена коэффициентов регрессии.

p = 3;
PriorMdl = bayeslm(p,'ModelType','diffuse','VarNames',["IPI" "E" "WR"])

PriorMdl = 
  diffuseblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}

 
           | Mean  Std        CI95        Positive        Distribution       
-----------------------------------------------------------------------------
 Intercept |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 IPI       |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 E         |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 WR        |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 Sigma2    |  Inf  Inf  [   NaN,    NaN]    1.000   Proportional to 1/Sigma2

PriorMdl diffuseblm объект модели.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда предиктора и ответа.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Оцените условное апостериорное распределение $β$ учитывая данные и это $σ^{2} = 2$ , и возвратите сводную таблицу оценки, чтобы получить доступ к оценкам.

[Mdl,SummaryBeta] = estimate(PriorMdl,X,y,'Sigma2',2);

Method: Analytic posterior distributions
Conditional variable: Sigma2 fixed at   2
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95         Positive     Distribution    
--------------------------------------------------------------------------------
 Intercept | -24.2536  1.8696  [-27.918, -20.589]    0.000   N (-24.25, 1.87^2) 
 IPI       |   4.3913  0.0301   [ 4.332,  4.450]     1.000   N (4.39, 0.03^2)   
 E         |   0.0011  0.0001   [ 0.001,  0.001]     1.000   N (0.00, 0.00^2)   
 WR        |   2.4682  0.0743   [ 2.323,  2.614]     1.000   N (2.47, 0.07^2)   
 Sigma2    |    2       0       [ 2.000,  2.000]     1.000   Fixed value

estimate отображает сводные данные условного апостериорного распределения $β$ . Поскольку $σ^{2}$ фиксируется в 2 во время оценки, выводы на ней тривиальны.

Извлеките вектор средних значений и ковариационную матрицу условного выражения, следующего из $β$ из сводной таблицы оценки.

condPostMeanBeta = SummaryBeta.Mean(1:(end - 1))

condPostMeanBeta = 4×1

  -24.2536
    4.3913
    0.0011
    2.4682

CondPostCovBeta = SummaryBeta.Covariances(1:(end - 1),1:(end - 1))

CondPostCovBeta = 4×4

    3.4956    0.0350   -0.0001    0.0241
    0.0350    0.0009   -0.0000   -0.0013
   -0.0001   -0.0000    0.0000   -0.0000
    0.0241   -0.0013   -0.0000    0.0055

Отобразите Mdl.

Mdl

Mdl = 
  diffuseblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}

 
           | Mean  Std        CI95        Positive        Distribution       
-----------------------------------------------------------------------------
 Intercept |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 IPI       |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 E         |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 WR        |  0    Inf  [   NaN,    NaN]    0.500   Proportional to one      
 Sigma2    |  Inf  Inf  [   NaN,    NaN]    1.000   Proportional to 1/Sigma2

Поскольку estimate вычисляет условное апостериорное распределение, оно возвращает исходную предшествующую модель, не следующее, в первом положении списка выходных аргументов.

Оцените условные апостериорные распределения $σ^{2}$ учитывая, что $β$ condPostMeanBeta.

[~,SummarySigma2] = estimate(PriorMdl,X,y,'Beta',condPostMeanBeta);

Method: Analytic posterior distributions
Conditional variable: Beta fixed at -24.2536       4.3913   0.00112035      2.46823
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95         Positive     Distribution    
--------------------------------------------------------------------------------
 Intercept | -24.2536   0      [-24.254, -24.254]    0.000   Fixed value        
 IPI       |   4.3913   0       [ 4.391,  4.391]     1.000   Fixed value        
 E         |   0.0011   0       [ 0.001,  0.001]     1.000   Fixed value        
 WR        |   2.4682   0       [ 2.468,  2.468]     1.000   Fixed value        
 Sigma2    |  48.5138  9.0088   [33.984, 69.098]     1.000   IG(31.00, 0.00069)

estimate отображает сводные данные условного апостериорного распределения $σ^{2}$ . Поскольку $β$ фиксируется к condPostMeanBeta во время оценки выводы на нем тривиальны.

Извлеките среднее значение и отклонение условного выражения, следующего из $σ^{2}$ из сводной таблицы оценки.

condPostMeanSigma2 = SummarySigma2.Mean(end)

condPostMeanSigma2 = 48.5138

CondPostVarSigma2 = SummarySigma2.Covariances(end,end)

CondPostVarSigma2 = 81.1581

Доступ к оценкам в отображении оценки

Скрипт Open Live Script

Считайте модель регрессии в Оценке Следующей Используя гамильтонов Сэмплер Монте-Карло. Этот пример использует те же данные и контекст, но принимает полусопряженную предшествующую модель вместо этого.

Создайте полусопряженную предшествующую модель для параметров линейной регрессии. Задайте количество предикторов p и имена коэффициентов регрессии.

p = 3;
PriorMdl = bayeslm(p,'ModelType','semiconjugate',...
    'VarNames',["IPI" "E" "WR"]);

PriorMdl semiconjugateblm объект модели.

Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда предиктора и ответа.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Оцените крайние апостериорные распределения $β$ и $σ^{2}$ .

rng(1); % For reproducibility
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y);

Method: Gibbs sampling with 10000 draws
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std          CI95        Positive  Distribution 
-------------------------------------------------------------------------
 Intercept | -23.9922  9.0520  [-41.734, -6.198]    0.005     Empirical  
 IPI       |   4.3929  0.1458   [ 4.101,  4.678]    1.000     Empirical  
 E         |   0.0011  0.0003   [ 0.000,  0.002]    0.999     Empirical  
 WR        |   2.4711  0.3576   [ 1.762,  3.178]    1.000     Empirical  
 Sigma2    |  46.7474  8.4550   [33.099, 66.126]    1.000     Empirical

PosteriorMdl empiricalblm объект модели, потому что крайние апостериорные распределения полусопряженных моделей аналитически тяжелы, таким образом, estimate должен реализовать сэмплер Гиббса. Summary таблица, содержащая оценки, и заключает тот estimate отображения в командной строке.

Отобразите сводную таблицу.

Summary

Summary=5×6 table
                   Mean          Std                  CI95              Positive    Distribution                                  Covariances                              
                 _________    __________    ________________________    ________    _____________    ______________________________________________________________________

    Intercept      -23.992         9.052       -41.734       -6.1976     0.0053     {'Empirical'}        81.938        0.81622     -0.0025308        0.58928              0
    IPI             4.3929       0.14578        4.1011        4.6782          1     {'Empirical'}       0.81622       0.021252    -7.1663e-06      -0.030939              0
    E            0.0011124    0.00033976    0.00045128     0.0017883     0.9989     {'Empirical'}    -0.0025308    -7.1663e-06     1.1544e-07    -8.4598e-05              0
    WR              2.4711        0.3576        1.7622        3.1781          1     {'Empirical'}       0.58928      -0.030939    -8.4598e-05        0.12788              0
    Sigma2          46.747         8.455        33.099        66.126          1     {'Empirical'}             0              0              0              0         71.487

Доступ к 95% equitailed вероятный интервал коэффициента регрессии IPI.

Summary.CI95(2,:)

ans = 1×2

    4.1011    4.6782

Входные параметры

свернуть все

`PriorMdl` — Байесова модель линейной регрессии
`conjugateblm` объект модели | `semiconjugateblm` объект модели | `diffuseblm` объект модели | `empiricalblm` объект модели | `customblm` объект модели

Байесова модель линейной регрессии представление предшествующей модели в виде объекта в этой таблице.

Объект модели	Описание
`conjugateblm`	Зависимый, нормальная обратная гамма спрягает модель, возвращенную `bayeslm` или `estimate`
`semiconjugateblm`	Независимый, нормальная обратная гамма полуспрягает модель, возвращенную `bayeslm`
`diffuseblm`	Рассейте предшествующую модель, возвращенную `bayeslm`
`empiricalblm`	Предшествующая модель, охарактеризованная выборками от предшествующих распределений, возвращенных `bayeslm` или `estimate`
`customblm`	Предшествующая функция распределения, которой вы объявляете возвращенный `bayeslm`

PriorMdl может также представлять объединенную следующую модель, возвращенную estimate, любой conjugateblm или empiricalblm объект модели. В этом случае, estimate обновляет объединенное апостериорное распределение с помощью новых наблюдений в X и y.

`X` — Данные о предикторе
числовая матрица

Данные о предикторе для модели многофакторной линейной регрессии в виде numObservations- PriorMdl.NumPredictors числовая матрица. numObservations количество наблюдений и должно быть равно длине y.

Типы данных: double

`y` — Данные об ответе
числовой вектор

Данные об ответе для модели многофакторной линейной регрессии в виде числового вектора с numObservations элементы.

Типы данных: double

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'Sigma2',2 задает оценку условного апостериорного распределения коэффициентов регрессии, учитывая данные и что заданным отклонением воздействия является 2.

Опции для всех предшествующих распределений

свернуть все

`'Display'` — Отметьте, чтобы отобразить Байесовы сводные данные средства оценки в командной строке
`true` (значение по умолчанию) | `false`

Отметьте, чтобы отобразить Байесовы сводные данные средства оценки в командной строке в виде разделенной запятой пары, состоящей из 'Display' и значение в этой таблице.

Значение	Описание
`true`	`estimate` информация об оценке печати и таблица, обобщающая Байесовы средства оценки к командной строке.
`false`	`estimate` не распечатывает к командной строке.

Информация об оценке включает метод оценки, зафиксированные параметры, количество наблюдений и количество предикторов. Сводная таблица содержит оцененные следующие средние значения и стандартные отклонения (квадратный корень из следующего отклонения), 95% equitailed вероятные интервалы, апостериорная вероятность, что параметр больше 0, и описание апостериорного распределения (если известный).

Если вы задаете один из Beta или Sigma2то estimate включает вашу спецификацию в отображение, и соответствующие следующие оценки тривиальны.

Пример: 'Display',false

Типы данных: логический

Опции для всех предшествующих распределений кроме эмпирического

свернуть все

`'Beta'` — Значение коэффициентов регрессии для условной оценки апостериорного распределения отклонения воздействия
пустой массив (`[]`) (значение по умолчанию) | числовой вектор-столбец

Значение коэффициентов регрессии для условной оценки апостериорного распределения отклонения воздействия в виде разделенной запятой пары, состоящей из 'Beta' и (PriorMdl.Intercept + PriorMdl.NumPredictors)-by-1 числовой вектор. estimate оценивает характеристики π (σ ^2|yX, β = Beta), где y yX X, и Beta значение 'Beta'. Если PriorMdl.Intercept true, затем Beta(1) соответствует точке пересечения модели. Все другие значения соответствуют переменным предикторам, которые составляют столбцы X\beta не может содержать NaN значения (то есть, все коэффициенты должны быть известны).

Вы не можете задать Beta и Sigma2 одновременно.

По умолчанию, estimate не вычисляет характеристики условного выражения, следующего из σ ².

Пример: 'Beta',1:3

Типы данных: double

`'Sigma2'` — Значение отклонения воздействия для условной оценки апостериорного распределения коэффициентов регрессии
пустой массив (`[]`) (значение по умолчанию) | положительный числовой скаляр

Значение отклонения воздействия для условной оценки апостериорного распределения коэффициентов регрессии в виде разделенной запятой пары, состоящей из 'Sigma2' и положительный числовой скаляр. estimate оценочные характеристики π (β |yX, Sigma2), где y yX X, и Sigma2 значение 'Sigma2'.

Вы не можете задать Sigma2 и Beta одновременно.

По умолчанию, estimate не вычисляет характеристики условного выражения, следующего из β.

Пример: 'Sigma2',1

Типы данных: double

Опции для полусопряженных, эмпирических, и пользовательских предшествующих распределений

свернуть все

`'NumDraws'` — Симуляция Монте-Карло настроила объем выборки
`1e5` (значение по умолчанию) | положительное целое число

Симуляция Монте-Карло настроила объем выборки в виде разделенной запятой пары, состоящей из 'NumDraws' и положительное целое число. estimate на самом деле чертит BurnIn + NumDraws*Thin выборки, но это основывает оценки от NumDraws выборки. Для получения дополнительной информации, на как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Если PriorMdl semiconjugateblm модель и вы задаете Beta или Sigma2, затем MATLAB^® игнорирует NumDraws.

Пример: 'NumDraws',1e7

Типы данных: double

Опции для полусопряженных и пользовательских предшествующих распределений

свернуть все

`'BurnIn'` — Количество ничьих, чтобы удалить с начала выборки Монте-Карло
5000 (значение по умолчанию) | неотрицательный скаляр

Количество ничьих, чтобы удалить с начала выборки Монте-Карло уменьшать переходные эффекты в виде разделенной запятой пары, состоящей из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации, на как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Чтобы помочь вам задать соответствующий размер электротермотренировки, определите степень переходного поведения в выборке Монте-Карло путем определения 'BurnIn',0, симуляция нескольких тысяч использования наблюдений simulate, и затем графический вывод путей.

Пример: 'BurnIn',0

Типы данных: double

`'Thin'` — Монте-Карло настроил множитель объема выборки
1 (значение по умолчанию) | положительное целое число

Монте-Карло настроил множитель объема выборки в виде разделенной запятой пары, состоящей из 'Thin' и положительное целое число.

Фактическим объемом выборки Монте-Карло является BurnIn + NumDraws*Thin. После отбрасывания выжигания дефектов, estimate отбрасывает каждый Thin– 1 чертит, и затем сохраняет следующее. Для получения дополнительной информации, на как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Уменьшать потенциальную большую последовательную корреляцию в выборке Монте-Карло или уменьшать потребление памяти ничьих, сохраненных в PosteriorMdl, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`'BetaStart'` — Начальные значения коэффициентов регрессии для выборки MCMC
числовой вектор-столбец

Начальные значения коэффициентов регрессии для выборки Цепи Маркова Монте-Карло (MCMC) в виде разделенной запятой пары, состоящей из 'BetaStart' и числовой вектор-столбец с (PriorMdl.Intercept + PriorMdl.NumPredictors) элементы. По умолчанию, BetaStart оценка обычных наименьших квадратов (OLS).

Совет

Хорошая практика должна запуститься estimate многократно с помощью различных начальных значений параметра. Проверьте, что решения от каждого запуска сходятся к подобным значениям.

Пример: 'BetaStart',[1; 2; 3]

Типы данных: double

`'Sigma2Start'` — Начальные значения отклонения воздействия для выборки MCMC
положительный числовой скаляр

Начальные значения отклонения воздействия для выборки MCMC в виде разделенной запятой пары, состоящей из 'Sigma2Start' и положительный числовой скаляр. По умолчанию, Sigma2Start остаточная среднеквадратическая ошибка OLS.

Совет

Пример: 'Sigma2Start',4

Типы данных: double

Опции для пользовательских предшествующих распределений

свернуть все

`'Reparameterize'` — Репараметризация σ ² как журнал (σ ²)
`false` (значение по умолчанию) | `true`

Репараметризация σ ² как журнал (σ ²) во время следующей оценки и симуляции в виде разделенной запятой пары, состоящей из 'Reparameterize' и значение в этой таблице.

Значение	Описание
`false`	`estimate` не повторно параметрирует σ ².
`true`	`estimate` повторно параметрирует σ ² как журнал (σ ²). `estimate` преобразует результаты назад в исходную шкалу и не изменяет функциональную форму `PriorMdl.LogPDF`.

Совет

Если вы испытываете числовую нестабильность во время следующей оценки или симуляции σ ², то задаете 'Reparameterize',true.

Пример: 'Reparameterize',true

Типы данных: логический

`'Sampler'` — Сэмплер MCMC
`'slice'` (значение по умолчанию) | `'metropolis'` | `'hmc'`

Сэмплер MCMC в виде разделенной запятой пары, состоящей из 'Sampler' и значение в этой таблице.

Значение	Описание
`'slice'`	Сэмплер среза
`'metropolis'`	Случайный сэмплер Столицы обхода
`'hmc'`	Сэмплер Гамильтонова Монте-Карло (HMC)

Совет

Увеличить качество MCMC чертит, настройте сэмплер.
1. Перед вызовом estimate, задайте настраивающиеся параметры и их значения при помощи sampleroptions. Например, чтобы задать ширину сэмплера среза widthИспользование:
  options = sampleroptions('Sampler',"slice",'Width',width);
2. Задайте объект, содержащий настраивающиеся технические требования параметра, возвращенные sampleroptions при помощи 'Options' аргумент пары "имя-значение". Например, чтобы использовать настраивающиеся технические требования параметра в options, задайте:
```
'Options',options
```
Если вы задаете сэмплер HMC, то лучшая практика состоит в том, чтобы предоставить градиент для некоторых переменных, по крайней мере. estimate обращается численный расчет любых недостающих частных производных (NaN значения) в векторе градиента.

Пример: 'Sampler',"hmc"

Типы данных: string

`'Options'` — Опции сэмплера
`[]` (значение по умолчанию) | массив структур

Опции сэмплера в виде разделенной запятой пары, состоящей из 'Options' и массив структур, возвращенный sampleroptions. Используйте 'Options' задавать сэмплер MCMC и его настраивающие значения параметров.

Пример: 'Options',sampleroptions('Sampler',"hmc")

Типы данных: struct

`'Width'` — Типичная ширина интервала выборки
положительный числовой скаляр | числовой вектор из положительных значений

Типичная ширина интервала выборки вокруг текущего значения в предельных распределениях для сэмплера среза в виде разделенной запятой пары, состоящей из 'Width' и положительный числовой скаляр или (PriorMdl.Intercept + PriorMdl.NumPredictors+ 1 )-by-1 числовой вектор из положительных значений. Первый элемент соответствует точке пересечения модели, если вы существуете в модели. Следующий PriorMdl.NumPredictors элементы соответствуют коэффициентам переменных предикторов, упорядоченных столбцами данных предиктора. Последний элемент соответствует отклонению модели.

Если Width скаляр, затем estimate применяет Width ко всему PriorMdl.NumPredictors + PriorMdl.Intercept+ 1 предельные распределения.
Если Width числовой вектор, затем estimate применяет первый элемент к точке пересечения (если вы существуете), следующий PriorMdl.NumPredictors элементы к коэффициентам регрессии, соответствующим переменным предикторам в X, и последний элемент к отклонению воздействия.
Если объем выборки (size(X,1)) меньше 100, затем Width 10 по умолчанию.
Если объем выборки - по крайней мере 100, то estimate наборы Width к вектору из соответствующих следующих стандартных отклонений по умолчанию, принимая рассеянную предшествующую модель (diffuseblm).

Типичная ширина сэмплера среза не влияет на сходимость выборки MCMC. Это действительно влияет на количество необходимых вычислений функции, то есть, КПД алгоритма. Если ширина слишком мала, то алгоритм может реализовать чрезмерное количество вычислений функции, чтобы определить соответствующую ширину выборки. Если ширина является слишком большой, то алгоритму придется уменьшить ширину к соответствующему размеру, который требует вычислений функции.

estimate отправляет Width к slicesample функция. Для получения дополнительной информации смотрите slicesample.

Совет

Для максимальной гибкости задайте ширину сэмплера среза width при помощи 'Options' аргумент пары "имя-значение". Например:
```
'Options',sampleroptions('Sampler',"slice",'Width',width)
```

Пример: 'Width',[100*ones(3,1);10]

Выходные аргументы

свернуть все

`PosteriorMdl` — Байесова модель линейной регрессии хранение характеристик распределения
`conjugateblm` объект модели | `semiconjugateblm` объект модели | `diffuseblm` объект модели | `empiricalblm` объект модели | `customblm` объект модели

Байесова модель линейной регрессии хранение характеристик распределения, возвращенных как conjugateblm, semiconjugateblm, diffuseblm, empiricalblm, или customblm объект модели.

Если вы не задаете ни один Beta или Sigma2 (их значениями является []то estimate обновляет предшествующую модель с помощью вероятности данных, чтобы сформировать апостериорное распределение. PosteriorMdl характеризует апостериорное распределение. Его тип объекта зависит от предшествующего типа модели (PriorMdl).

Объект модели	`PriorMdl`
`conjugateblm`	`conjugateblm` или `diffuseblm`
`empiricalblm`	`semiconjugateblm`, `empiricalblm`, или `customblm`

Если вы задаете любой Beta или Sigma2, затем PosteriorMdl равняется PriorMdl (эти две модели являются тем же объектом, хранящим те же значения свойств). estimate не обновляет предшествующую модель, чтобы сформировать следующую модель. Однако estBeta, EstBetaCov, estSigma2, estSigma2Var, и Summary сохраните условные следующие оценки.

Для получения дополнительной информации об отображении PosteriorMdl, смотрите Summary.

Для получения дополнительной информации на поддерживаемых апостериорных распределениях, которые аналитически послушны, смотрите Аналитически Послушное Последующее поколение.

`Summary` — Сводные данные Байесовых средств оценки
таблица

Сводные данные Байесовых средств оценки, возвращенных как таблица. Summary содержит ту же информацию как отображение сводных данных оценки (Display). Строки соответствуют параметрам, и столбцы соответствуют этим следующим характеристикам для каждого параметра:

Mean – Следующее среднее значение
Std – Следующее стандартное отклонение
CI95 – 95% equitailed вероятный интервал
Positive – Апостериорная вероятность параметр больше 0
Distribution – Описание крайнего или условного апостериорного распределения параметра, когда известный
Covariances – Предполагаемая ковариационная матрица коэффициентов и отклонения воздействия

Имена строки являются именами в PriorMdl.VarNames. Именем последней строки является Sigma2.

В качестве альтернативы передайте PosteriorMdl к summarize получить сводные данные Байесовых средств оценки.

Ограничения

Если PriorMdl empiricalblm объект модели. Вы не можете задать Beta или Sigma2. Вы не можете оценить условные апостериорные распределения при помощи эмпирического предшествующего распределения.

Больше о

свернуть все

Байесова модель линейной регрессии

Bayesian linear regression model обрабатывает параметры β и σ ² в модели _yt многофакторной линейной регрессии (MLR) = _xt β + _εt как случайные переменные.

В течение многих времен t = 1..., T:

_yt является наблюдаемым ответом.
_xt является 1 на (p + 1) вектор-строка из наблюдаемых величин предикторов p. Вмещать точку пересечения модели, x _1t = 1 для всего t.
β (p + 1)-by-1 вектор-столбец коэффициентов регрессии, соответствующих переменным, которые составляют столбцы _xt.
_εt является случайным воздействием со средним значением нуля и Cov (ε) = σ ^2IT×_T, в то время как ε является T-by-1 вектор, содержащий все воздействия. Эти предположения подразумевают, что вероятность данных

$ℓ (β, σ^{2} | y, x) = \prod_{t = 1}^{T} ϕ (y_{t}; x_{t} β, σ^{2}) .$
ϕ (_yt; _xtβ, σ ²) является Гауссовой плотностью вероятности со средним _xtβ и отклонением σ ² оцененных в _yt;.

Прежде, чем рассмотреть данные, вы налагаете предположение joint prior distribution на (β, σ ²). В Байесовом анализе вы обновляете распределение параметров при помощи информации о параметрах, полученных из вероятности данных. Результатом является joint posterior distribution (β, σ ²) или conditional posterior distributions параметров.

Советы

Симуляция Монте-Карло подвергается изменению. Если estimate симуляция Монте-Карло использования, затем оценивает, и выводы могут варьироваться, когда вы вызываете estimate многократно при на вид эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите seed случайных чисел при помощи rng перед вызовом estimate.
Если estimate выдает ошибку при оценке, что апостериорное распределение с помощью пользовательской предшествующей модели, затем пытается настроить начальные значения параметров при помощи BetaStart или Sigma2Start, или попытайтесь настроить заявленный журнал предшествующая функция, и затем восстановить модель. Ошибка может указать, что журналом предшествующего распределения является –Inf в заданных начальных значениях.

Алгоритмы

Каждый раз, когда предшествующее распределение (PriorMdl) и вероятность данных дает к аналитически послушному апостериорному распределению, estimate оценивает решения закрытой формы средств оценки Бейеса. В противном случае, estimate обращения к симуляции Монте-Карло, чтобы оценить параметры и чертить выводы. Для получения дополнительной информации смотрите Следующую Оценку и Вывод.
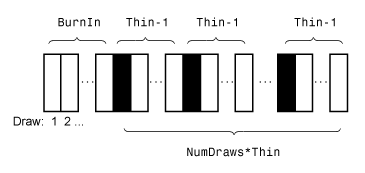
Этот рисунок иллюстрирует как estimate уменьшает выборку Монте-Карло использование значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные ничьи от распределения. estimate удаляет белые прямоугольники из выборки Монте-Карло. Остающийся NumDraws черные прямоугольники составляют выборку Монте-Карло.

Вопросы совместимости

развернуть все

`estimate` возвращает только предполагаемый объект модели и сводные данные оценки

Ошибки, запускающиеся в R2019b

Для более простого интерфейса, estimate возвращает только предполагаемую модель и сводную таблицу оценки. Теперь поддерживаемые синтаксисы:

PosteriorMdl = estimate(...);
[PosteriorMdl,Summary] = estimate(...);

Можно получить оцененные следующие средние значения и ковариации, на основе предельных или условных распределений, из сводной таблицы оценки.

В прошлых релизах, estimate возвращенный эти выходные аргументы:

[PosteriorMdl,estBeta,EstBetaCov,estSigma2,estSigma2Var,Summary] = estimate(...);

estBeta, EstBetaCov, estSigma2, и estSigma2Var следующие средние значения и ковариации β и σ ².

Запуск в R2019b, если вы запрашиваете какой-либо выходной аргумент в положении, больше, чем второе положение, estimate проблемы эта ошибка:

Too many output arguments.

Для получения дополнительной информации о том, как обновить ваш код, смотрите Заменяющий Удаленные Синтаксисы оценки.

Смотрите также

Объекты

conjugateblm | customblm | diffuseblm | empiricalblm | semiconjugateblm

Документация

estimate

Синтаксис

Описание

Примеры

Сравните предшествующую и крайнюю следующую оценку по умолчанию оценками OLS

Оцените следующий Используя гамильтонов сэмплер Монте-Карло

Оцените условные апостериорные распределения

Доступ к оценкам в отображении оценки

Входные параметры

`PriorMdl` — Байесова модель линейной регрессии
`conjugateblm` объект модели | `semiconjugateblm` объект модели | `diffuseblm` объект модели | `empiricalblm` объект модели | `customblm` объект модели

`X` — Данные о предикторе
числовая матрица

`y` — Данные об ответе
числовой вектор

Аргументы в виде пар имя-значение

`'Display'` — Отметьте, чтобы отобразить Байесовы сводные данные средства оценки в командной строке
`true` (значение по умолчанию) | `false`

`'NumDraws'` — Симуляция Монте-Карло настроила объем выборки
`1e5` (значение по умолчанию) | положительное целое число

`'BurnIn'` — Количество ничьих, чтобы удалить с начала выборки Монте-Карло
5000 (значение по умолчанию) | неотрицательный скаляр

`'Thin'` — Монте-Карло настроил множитель объема выборки
1 (значение по умолчанию) | положительное целое число

`'BetaStart'` — Начальные значения коэффициентов регрессии для выборки MCMC
числовой вектор-столбец

`'Sigma2Start'` — Начальные значения отклонения воздействия для выборки MCMC
положительный числовой скаляр

`'Reparameterize'` — Репараметризация σ ² как журнал (σ ²)
`false` (значение по умолчанию) | `true`

`'Sampler'` — Сэмплер MCMC
`'slice'` (значение по умолчанию) | `'metropolis'` | `'hmc'`

`'Options'` — Опции сэмплера
`[]` (значение по умолчанию) | массив структур

`'Width'` — Типичная ширина интервала выборки
положительный числовой скаляр | числовой вектор из положительных значений

Выходные аргументы

`Summary` — Сводные данные Байесовых средств оценки
таблица

Ограничения

Больше о

Байесова модель линейной регрессии

Советы

Алгоритмы

Вопросы совместимости

`estimate` возвращает только предполагаемый объект модели и сводные данные оценки

Смотрите также

Объекты

Функции

Темы

Документация Econometrics Toolbox

Поддержка

Документация

estimate

Синтаксис

Описание

Примеры

Сравните предшествующую и крайнюю следующую оценку по умолчанию оценками OLS

Оцените следующий Используя гамильтонов сэмплер Монте-Карло

Оцените условные апостериорные распределения

Доступ к оценкам в отображении оценки

Входные параметры

PriorMdl — Байесова модель линейной регрессии conjugateblm объект модели | semiconjugateblm объект модели | diffuseblm объект модели | empiricalblm объект модели | customblm объект модели

X — Данные о предикторе числовая матрица

y — Данные об ответе числовой вектор

Аргументы в виде пар имя-значение

'Display' — Отметьте, чтобы отобразить Байесовы сводные данные средства оценки в командной строке true (значение по умолчанию) | false

'NumDraws' — Симуляция Монте-Карло настроила объем выборки 1e5 (значение по умолчанию) | положительное целое число

'BurnIn' — Количество ничьих, чтобы удалить с начала выборки Монте-Карло5000 (значение по умолчанию) | неотрицательный скаляр

'Thin' — Монте-Карло настроил множитель объема выборки1 (значение по умолчанию) | положительное целое число

'BetaStart' — Начальные значения коэффициентов регрессии для выборки MCMC числовой вектор-столбец

'Sigma2Start' — Начальные значения отклонения воздействия для выборки MCMC положительный числовой скаляр

'Reparameterize' — Репараметризация σ 2 как журнал (σ 2) false (значение по умолчанию) | true

'Sampler' — Сэмплер MCMC 'slice' (значение по умолчанию) | 'metropolis' | 'hmc'

'Options' — Опции сэмплера [] (значение по умолчанию) | массив структур

'Width' — Типичная ширина интервала выборки положительный числовой скаляр | числовой вектор из положительных значений

Выходные аргументы

Summary — Сводные данные Байесовых средств оценки таблица

Ограничения

Больше о

Байесова модель линейной регрессии

Советы

Алгоритмы

Вопросы совместимости

estimate возвращает только предполагаемый объект модели и сводные данные оценки

Смотрите также

Объекты

Функции

Темы

Документация Econometrics Toolbox

Поддержка

`PriorMdl` — Байесова модель линейной регрессии
`conjugateblm` объект модели | `semiconjugateblm` объект модели | `diffuseblm` объект модели | `empiricalblm` объект модели | `customblm` объект модели

`X` — Данные о предикторе
числовая матрица

`y` — Данные об ответе
числовой вектор

`'Display'` — Отметьте, чтобы отобразить Байесовы сводные данные средства оценки в командной строке
`true` (значение по умолчанию) | `false`

`'NumDraws'` — Симуляция Монте-Карло настроила объем выборки
`1e5` (значение по умолчанию) | положительное целое число

`'BurnIn'` — Количество ничьих, чтобы удалить с начала выборки Монте-Карло
5000 (значение по умолчанию) | неотрицательный скаляр

`'Thin'` — Монте-Карло настроил множитель объема выборки
1 (значение по умолчанию) | положительное целое число

`'BetaStart'` — Начальные значения коэффициентов регрессии для выборки MCMC
числовой вектор-столбец

`'Sigma2Start'` — Начальные значения отклонения воздействия для выборки MCMC
положительный числовой скаляр

`'Reparameterize'` — Репараметризация σ ² как журнал (σ ²)
`false` (значение по умолчанию) | `true`

`'Sampler'` — Сэмплер MCMC
`'slice'` (значение по умолчанию) | `'metropolis'` | `'hmc'`

`'Options'` — Опции сэмплера
`[]` (значение по умолчанию) | массив структур

`'Width'` — Типичная ширина интервала выборки
положительный числовой скаляр | числовой вектор из положительных значений

`Summary` — Сводные данные Байесовых средств оценки
таблица

`estimate` возвращает только предполагаемый объект модели и сводные данные оценки