Предскажите ответы Байесовой модели линейной регрессии
yF = forecast(Mdl,XF)numPeriods предсказанные ответы из Байесовой модели
Mdl линейной регрессии учитывая данные о предикторе в XF, матрица с numPeriods 'Строки' .
Оценить прогноз, forecast использует среднее значение numPeriods- размерное следующее прогнозирующее распределение.
Если Mdl объединенная предшествующая модель (возвращенный bayeslmто forecast использование только объединенное предшествующее распределение и инновационное распределение, чтобы сформировать прогнозирующее распределение.
Если Mdl следующая модель (возвращенный estimateто forecast использует следующее прогнозирующее распределение.
NaNs в данных указывают на отсутствующие значения, который forecast удаляет использующее мудрое списком удаление.
yF = forecast(Mdl,XF,X,y)X и соответствующие данные об ответе y.
Если Mdl объединенная предшествующая модель, затем forecast производит следующее прогнозирующее распределение путем обновления предшествующей модели с информацией о параметрах, которые это получает из данных.
Если Mdl следующая модель, затем forecast обновляет последующее поколение с информацией о параметрах, которые она получает из дополнительных данных. Вероятность полных данных состоит из дополнительных данных X и y, и данные, которые создали Mdl.
yF = forecast(___,Name,Value)
Если Mdl empiricalblm объект модели, затем вы не можете задать Beta или Sigma2. Вы не можете предсказать от условных прогнозирующих распределений при помощи эмпирического предшествующего распределения.
Симуляция Монте-Карло подвергается изменению. Если forecast симуляция Монте-Карло использования, затем оценивает, и выводы могут варьироваться, когда вы вызываете forecast многократно при на вид эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите seed случайных чисел при помощи rng перед вызовом forecast.
Если forecast выдает ошибку при оценке, что апостериорное распределение с помощью пользовательской предшествующей модели, затем пытается настроить начальные значения параметров при помощи BetaStart или Sigma2Start, или попытайтесь настроить заявленный журнал предшествующая функция, и затем восстановить модель. Ошибка может указать, что журналом предшествующего распределения является –Inf в заданных начальных значениях.
К предсказанным ответам от условного следующего прогнозирующего распределения аналитически тяжелых моделей, кроме эмпирических моделей, передают ваш предшествующий объект модели и выборочные данные оценки к forecast. Затем задайте Beta аргумент пары "имя-значение", чтобы предсказать от условного выражения, следующего из σ 2 или задать Sigma2 аргумент пары "имя-значение", чтобы предсказать от условного выражения, следующего из β.
Каждый раз, когда forecast должен оценить апостериорное распределение (например, когда Mdl представляет предшествующее распределение, и вы предоставляете X и y) и следующее аналитически послушно, forecast оценивает решения закрытой формы средств оценки Бейеса. В противном случае, forecast обращения к симуляции Монте-Карло, чтобы предсказать при помощи следующего прогнозирующего распределения. Для получения дополнительной информации смотрите Следующую Оценку и Вывод.
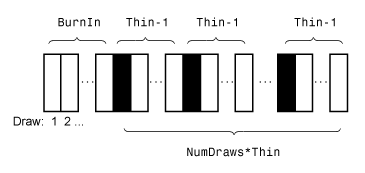
Этот рисунок иллюстрирует как forecast уменьшает выборку Монте-Карло использование значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные ничьи от распределения. forecast удаляет белые прямоугольники из выборки Монте-Карло. Остающийся NumDraws черные прямоугольники составляют выборку Монте-Карло.
conjugateblm | customblm | diffuseblm | empiricalblm | lassoblm | mixconjugateblm | mixsemiconjugateblm | semiconjugateblm