На следующем рисунке показана блок-схема Simulink ®, показывающая проблему отслеживания в конструкции автопилота самолета. Чтобы открыть эту схему, введитеlqrpilot в подсказке MATLAB ®.
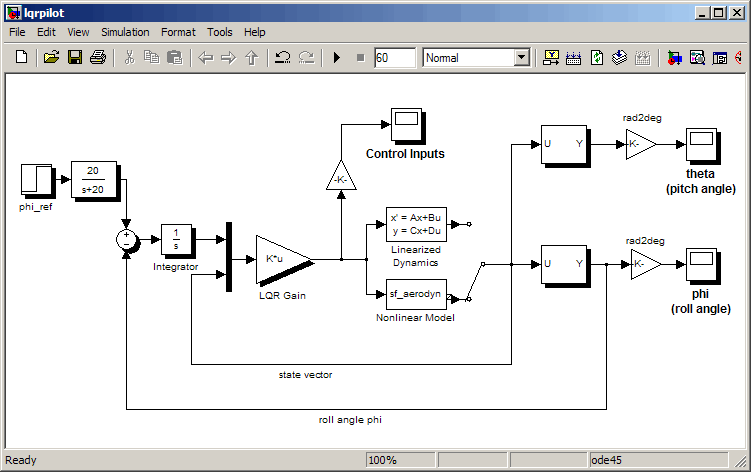
Ниже перечислены основные особенности этой схемы.
Блок линеаризованной динамики содержит линеаризованный корпус самолета.
sf_aerodyn S-функциональный-блок, который содержит нелинейные уравнения для ∘).
Сигнал об ошибке, передаваемый между «» Это помогает привести ошибку к нулю.
Начиная со стандартного уравнения «состояние-пространство»
где
r,
Переменные u, v и w представляют собой три скорости относительно корпуса, показанные следующим образом.
Рамка координат тела для летательного аппарата
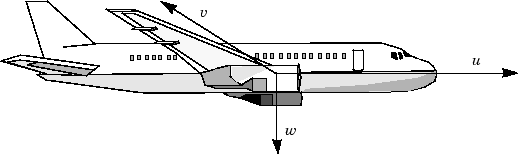
Переменные - это крен и тангаж, а p, q и r - скорости крена, тангажа и рыскания, соответственно.
Динамика планера нелинейна. Следующее уравнение показывает нелинейные компоненты, добавленные в уравнение пространства состояний.
Нелинейная составляющая уравнения состояния-пространства
⋅tanθ]
Для просмотра числовых значений для A и B введите
load lqrpilot A, B
по запросу MATLAB.
В конструкциях LQG нелинейная динамика обрезается при нулевом значении ϕ=15∘ и p, q, r и start. Поскольку u, v и w не входят в нелинейный член на предыдущем рисунке, это равносильно линеаризации вокруг 0,15∘) со всеми остальными состояниями, установленными на ноль. Результирующая матрица состояния линеаризованной модели называется A15.
Цель выполнения устойчивого скоординированного поворота, как показано на этом рисунке.
Самолет делает поворот на 60 °
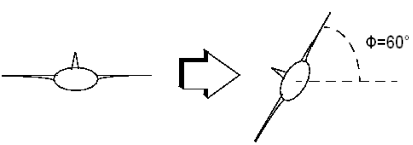
Для достижения этой цели необходимо разработать контроллер, который будет управлять постоянным поворотом, проходя через 60 ° крен. Кроме того, предположим, что для того, чтобы оставаться как можно ближе к нулю, требуется λ, угол тангажа.
Для вычисления матрицы усиления LQG, K, тип
lqrdes
по запросу MATLAB. Затем запустите lqrpilot модель с нелинейной моделью, sf_aerodyn, выбрано.
На этом рисунке показан ответ, полученный выполнении команды 60 ° step.
Отслеживание команды Rolle Step
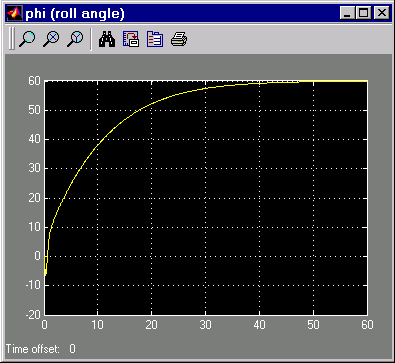
Как вы видите, система отслеживает рулон 60 ° примерно за 60 секунд.
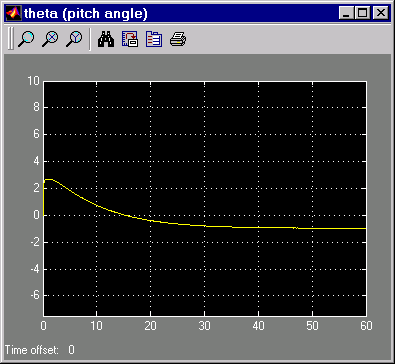
Другая цель состояла в том, чтобы держать θ, угол подачи, относительно маленький. На этом рисунке показано, насколько хорошо это сделал контроллер LQG.
Минимизация смещения в углу шага, тета
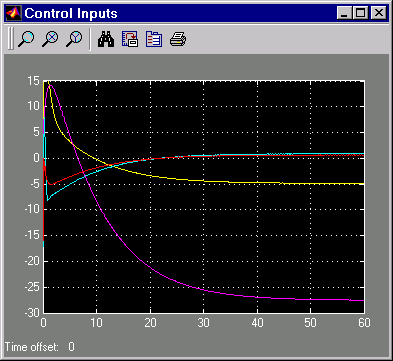
Наконец, на этом рисунке показаны управляющие входные сигналы.
Управляющие входы для проблемы отслеживания LQG
Попробуйте настроить Q и R матрицы в lqrdes.m и проверка контрольных входов и состояния системы, проверка повторного запуска lqrdes для обновления матрицы усиления LQG K. С помощью проб и ошибок можно увеличить время отклика этой конструкции. Кроме того, сравните линейные и нелинейные конструкции, чтобы увидеть влияние нелинейности на производительность системы.