Линейно-квадратично-гауссово (LQG) управление - современная государственно-пространственная техника для проектирования оптимальных динамических регуляторов и сервоконтроллеров с интегральным действием (также известных как трекеры уставок). Этот метод позволяет отличать эффективность регулирования/трекера и усилия по управлению, а также учитывать нарушения технологического процесса и шум измерений.
Для проектирования регуляторов LQG и датчиков уставок необходимо выполнить следующие шаги:
Создайте оптимальный коэффициент усиления LQ.
Создайте фильтр Калмана (блок оценки состояния).
Создайте конструкцию LQG, подключив оптимальный коэффициент усиления LQ и фильтр Калмана.
Дополнительные сведения об использовании конструкции LQG для создания регуляторов LQG см. в разделе Линейная-квадратично-гауссова (LQG) Конструкция для регулирования.
Дополнительные сведения об использовании конструкции LQG для создания сервоконтроллеров LQG см. в разделе Linear-Quadratic-Gaussian (LQG) Design of Servo Controller with Integral Action.
Эти темы посвящены случаю непрерывного времени. Для получения информации о конструкции дискретного LQG см. dlqr и kalman справочные страницы.
Можно сконструировать регулятор LQG для регулирования выхода y вокруг нуля в следующей модели.
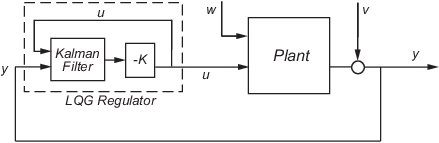
Установка в этой модели испытывает возмущения (технологический шум) w и управляется органами управления u. Регулятор полагается на шумные измерения y для создания этих органов управления. Состояние установки и уравнения измерения принимают форму
и w и v смоделированы как белый шум.
Примечание
Для проектирования LQG требуется государственно-космическая модель установки. Вы можете использовать ss преобразование других форматов модели в пространство состояний.
Для проектирования регуляторов LQG можно использовать методы проектирования, показанные в следующей таблице.
| Для проектирования регулятора LQG с использованием... | Используйте следующие команды: |
|---|---|
|
Быстрая, одноступенчатая методика проектирования, если верно следующее:
| lqg |
|
Более гибкая, трехшаговая техника проектирования, позволяющая указать:
|
Дополнительные сведения см. в разделе
|
Оптимальный коэффициент усиления LQ строится из следующих элементов:
Для построения оптимального коэффициента усиления введите следующую команду:
K= lqr(A,B,Q,R,N)
Эта команда вычисляет матрицу оптимального усиления K, для которого закон обратной связи состояния Kx минимизирует следующую квадратичную функцию затрат на непрерывное время:
=∫0∞{xTQx+2xTNu+uTRu}dt
Программа вычисляет матрицу K усиления, решая алгебраическое уравнение Риккати.
Для получения информации о построении LQ-оптимального усиления, включая функцию затрат, которую программное обеспечение минимизирует в течение дискретного времени, см. lqr справочная страница.
Для регулирования LQG и сервоуправления необходим оценщик состояния Калмана, поскольку невозможно реализовать оптимальную LQ-оптимальную обратную связь состояния без полного измерения состояния.
Оценка состояния ^ строится таким образом, что Kx ^ остается оптимальной для задачи «выход-обратная связь». Коэффициент усиления оценщика состояния Калмана строится из следующих элементов:
Примечание
Оценщик состояния Калмана строится одинаково как для регулирования, так и для сервоконтроля.
Для построения оценщика состояния Калмана введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет оценщик состояния Калмана, kest со следующими уравнениями растений:
где w и v смоделированы как белый шум. L является выигрышем Калмана и P ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью фильтра Калмана
y − Cx ^ − Du)
с входами u (органы управления) и y (измерения). Данные ковариации шума
wvT) = Nn
определяет коэффициент усиления Калмана L через алгебраическое уравнение Риккати.
Фильтр Калмана является оптимальным оценщиком при работе с гауссовым белым шумом. В частности, он минимизирует асимптотическую ковариацию
limt→∞E − x ^) T)
ошибки оценки x ^.
![]()
Дополнительные сведения см. в разделе kalman справочная страница. Полный пример реализации фильтра Калмана см. в разделе Фильтрация Калмана.
Для формирования регулятора LQG подключите фильтр Калмана kest и оптимальный коэффициент усиления LQ K путем ввода следующей команды:
regulator = lqgreg(kest, K);
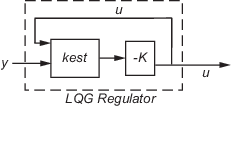
Регулятор имеет следующие уравнения состояния-пространства:
x ^ + Lyu = − Kx ^
Для получения дополнительной информации о формировании регуляторов LQG см. lqgreg и LQG Regulation: История успеха прокатного стана.
Можно создать сервоконтроллер с интегральным действием для следующей модели:
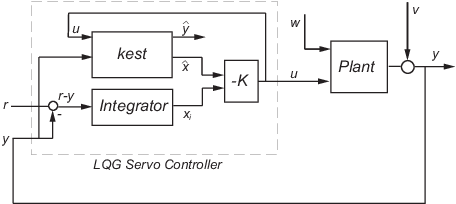
Разработанный сервоконтроллер гарантирует, что выходной сигнал y отслеживает опорную команду r при отклонении возмущений процесса w и шума измерения v.
Установка на предыдущем рисунке подвержена возмущениям w и приводится в действие регуляторами u. Для формирования этих элементов управления сервоконтроллер использует шумные измерения y. Состояние установки и уравнения измерения имеют вид
и w и v смоделированы как белый шум.
Примечание
Для проектирования LQG требуется государственно-космическая модель установки. Вы можете использовать ss преобразование других форматов модели в пространство состояний.
Для конструирования сервоконтроллеров LQG можно использовать методы конструирования, показанные в следующей таблице.
| Для проектирования сервоконтроллера LQG с помощью... | Используйте следующие команды: |
|---|---|
|
Быстрая, одноступенчатая методика проектирования, если верно следующее:
| lqg |
|
Более гибкая, трехшаговая техника проектирования, позволяющая указать:
|
Дополнительные сведения см. в разделе
|
Создается оптимальный коэффициент усиления LQ из
Модель государственно-космического завода sys
Матрицы взвешивания Q, R, и N, которые определяют компромисс между производительностью трекера и усилиями по управлению
Для построения оптимального коэффициента усиления введите следующую команду:
K= lqi(sys,Q,R,N)
Эта команда вычисляет матрицу оптимального усиления K, для которого закон обратной связи состояния [x; xi] минимизирует следующую квадратичную функцию затрат на непрерывное время:
=∫0∞{zTQz+uTRu+2zTNu}dt
Программа вычисляет матрицу K усиления, решая алгебраическое уравнение Риккати.
Для получения информации о построении LQ-оптимального усиления, включая функцию затрат, которую программное обеспечение минимизирует в течение дискретного времени, см. lqi справочная страница.
Для регулирования LQG и сервоконтроля необходим оценщик состояния Калмана, поскольку невозможно реализовать оптимальную для LQ обратную связь состояния без полного измерения состояния.
Оценка состояния ^ строится таким образом, что Kx ^ остается оптимальной для задачи «выход-обратная связь». Коэффициент усиления оценщика состояния Калмана строится из следующих элементов:
Примечание
Оценщик состояния Калмана строится одинаково как для регулирования, так и для сервоконтроля.
Для построения оценщика состояния Калмана введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет оценщик состояния Калмана, kest со следующими уравнениями растений:
где w и v смоделированы как белый шум. L является выигрышем Калмана и P ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью фильтра Калмана
y − Cx ^ − Du)
с входами u (органы управления) и y (измерения). Данные ковариации шума
wvT) = Nn
определяет коэффициент усиления Калмана L через алгебраическое уравнение Риккати.
Фильтр Калмана является оптимальным оценщиком при работе с гауссовым белым шумом. В частности, он минимизирует асимптотическую ковариацию
limt→∞E − x ^) T)
ошибки оценки x ^.
![]()
Дополнительные сведения см. в разделе kalman справочная страница. Полный пример реализации фильтра Калмана см. в разделе Фильтрация Калмана.
Для формирования сервоконтроллера LQG с двумя степенями свободы подключите фильтр Калмана kest и оптимальный коэффициент усиления LQ K путем ввода следующей команды:
servocontroller = lqgtrack(kest, K);
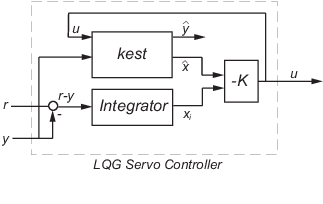
Сервоконтроллер имеет следующие уравнения состояния-пространства:
Kx − Ki] [x ^ xi]
Для получения дополнительной информации о формировании сервоконтроллеров LQG, в том числе о том, как сформировать сервоконтроллер LQG с одной степенью свободы, см. lqgtrack справочная страница.
kalman | lqg | lqgreg | lqgtrack | lqi | lqr