Exponenta Banner
exponenta event banner

Проектирование сервоконтроллера LQG

В этом примере показано, как сконструировать сервоконтроллер для следующей системы.

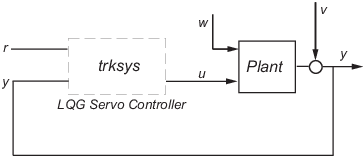
Установка имеет три состояния (x), два управляющих входа (u), два случайных входа (w), один выход (y), шум измерения для выхода (v) и следующие уравнения состояния и измерения:

x˙=Ax+Bu+Gwy=Cx+Du+Hw+v

где

A = [010001100] B = [0,3101 − 0,30,9] G = [− 0,71,12 − 1,1710,141,5] C = [1,91,31] D = [0,53 − 0,61] H = [− 1,2 − 0,89]

Система имеет следующие данные ковариации шума:

Qn = E (wwT) = [4221] Rn = E (vvT) = 0,7

Используйте следующую функцию затрат, чтобы определить компромисс между производительностью трекера и усилиями по управлению:

J (u) =∫0∞ (0 .1xTx + x2 + uT [1002] u) dt

Для проектирования сервоконтроллера LQG для этой системы:

  1. Создайте систему пространств состояний, введя в окне команд MATLAB следующее:

    A = [0 1 0;0 0 1;1 0 0];    
B = [0.3 1;0 1;-0.3 0.9];
G = [-0.7 1.12; -1.17 1; .14 1.5];
C = [1.9 1.3 1];  
D = [0.53 -0.61];
H = [-1.2 -0.89];
sys = ss(A,[B G],C,[D H]);

  2. Создайте оптимальный коэффициент усиления обратной связи по состоянию с использованием данной функции затрат, введя следующие команды:

    nx = 3;    %Number of states
ny = 1;    %Number of outputs
Q = blkdiag(0.1*eye(nx),eye(ny));
R = [1 0;0 2];
K = lqi(ss(A,B,C,D),Q,R);

  3. Создайте оценщик состояния Калмана, используя заданные данные ковариации шума, введя следующие команды:

    Qn = [4 2;2 1]; 
Rn = 0.7;
kest = kalman(sys,Qn,Rn);

  4. Подключите устройство оценки состояния Калмана и оптимальный коэффициент усиления обратной связи для формирования сервоконтроллера LQG, введя следующую команду:

    trksys = lqgtrack(kest,K)
    Эта команда возвращает следующий контроллер сервопривода LQG:
    >> trksys = lqgtrack(kest,K)
 
a = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -2.373  -1.062  -1.649   0.772
   x2_e  -3.443  -2.876  -1.335  0.6351
   x3_e  -1.963  -2.483  -2.043  0.4049
   xi1        0       0       0       0
 
b = 
             r1      y1
   x1_e       0  0.2849
   x2_e       0  0.7727
   x3_e       0  0.7058
   xi1        1      -1
 
c = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
d = 
       r1  y1
   u1   0   0
   u2   0   0
 
Input groups:              
       Name        Channels
     Setpoint         1    
    Measurement       2    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

См. также

| |

Связанные темы

Документация по панели инструментов системы управления

Поддержка