В качестве примера конструкции LQG рассмотрим следующую проблему регулирования.
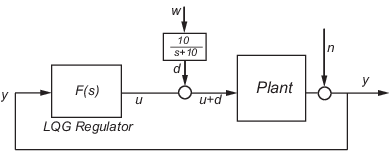
Цель состоит в том, чтобы регулировать производительность установки y около нуля. Входное возмущение d является низкочастотным со спектральной плотностью мощности (PSD), сконцентрированной ниже 10 рад/с. Для целей проектирования LQG он моделируется как белый шум, возбуждающий фильтр нижних частот с отсечкой 10 рад/с, как показано на следующем рисунке.
![]()
Для простоты этот шум моделируется как гауссовский белый шум с дисперсией 1.
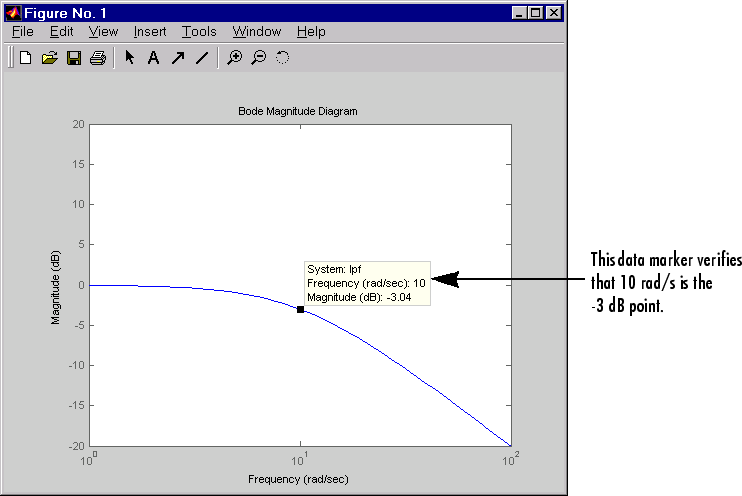
На следующем рисунке показана величина Боде формирующего фильтра.
Величина мода фильтра нижних частот
Существует некоторый измерительный шум n, с интенсивностью шума, заданной
0,01
использовать функцию затрат;
u2) dt
определить компромисс между эффективностью регулирования и стоимостью контроля. Следующие уравнения представляют модель состояния-пространства с разомкнутым контуром:
измерения)
где (A, B, C) - реализация состояния-пространства + 100).
Для решения этой проблемы оптимальным регулятором (регуляторами) LQG являются следующие команды:
sys = ss(tf(100,[1 1 100])) % State-space plant model % Design LQ-optimal gain K K = lqry(sys,10,1) % u = -Kx minimizes J(u) % Separate control input u and disturbance input d P = sys(:,[1 1]); % input [u;d], output y % Design Kalman state estimator Kest. Kest = kalman(P,1,0.01) % Form LQG regulator = LQ gain + Kalman filter. F = lqgreg(Kest,K)
Эти команды возвращают модель состояния-пространства F регулятора F (ов) LQG. lqry, kalman, и lqgreg функции при применении их к дискретным установкам выполняют дискретно-временную конструкцию LQG.
Чтобы проверить проект, закройте цикл с помощью feedback, создайте и добавьте фильтр нижних частот последовательно с системой с замкнутым контуром и сравните импульсные отклики с разомкнутым и замкнутым контуром, используя impulse функция.
% Close loop
clsys = feedback(sys,F,+1)
% Note positive feedback.
% Create the lowpass filter and add it in series with clsys.
s = tf('s');
lpf= 10/(s+10) ;
clsys_fin = lpf*clsys;
% Open- vs. closed-loop impulse responses
impulse(sys,'r--',clsys_fin,'b-')
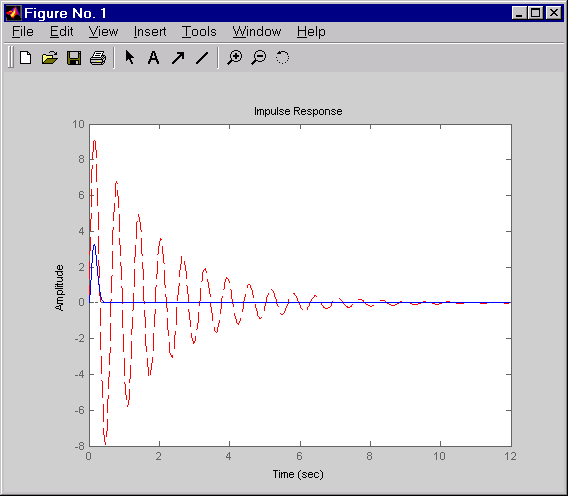
Эти команды создают следующий рисунок, на котором сравниваются импульсные отклики с разомкнутым и замкнутым контуром для этого примера.
Сравнение импульсной характеристики с разомкнутым и замкнутым контуром