Линейные модели (LTI)

Что такое растение?

Обычно инженеры по управлению начинают с разработки математического описания динамической системы, которой они хотят управлять. Управляемая система называется заводом. В качестве примера установки в этом разделе используется двигатель постоянного тока. В этом разделе описываются дифференциальные уравнения, описывающие электромеханические свойства двигателя постоянного тока с инерционной нагрузкой. Затем показано, как использовать функции Toolbox™ системы управления для построения линейных моделей на основе этих уравнений.

Представления линейной модели

Функции панели инструментов системы управления можно использовать для создания следующих представлений модели:

Модели пространства состояний (SS) формы
$\begin{array}{l} \frac{}{dxdt} = Ax \\ + Купить = \end{array}$ Cx + Du
где A, B, C и D - матрицы соответствующих размеров, x - вектор состояния, а u и y - входной и выходной векторы.
Передаточные функции (TF), например,
$H (s) \frac{=}{s^{} + 2s2}$ + s + 10
Модели с нулевым коэффициентом усиления (ZPK), например,
$H (z) \frac{= 3 (z + 1 + j}{) (z + 1 - j)}$ (z + 0,2) (z + 0,1)
Модели данных частотной характеристики (FRD), которые состоят из выборочных измерений частотной характеристики системы. Например, можно сохранить экспериментально собранные данные частотной характеристики в модели FRD.
Примечание
Дизайн моделей FRD является специализированным предметом, который эта тема не затрагивает. Обсуждение этой темы см. в разделе Модели данных частотного отклика (FRD).

Пример SISO: двигатель постоянного тока

Простая модель двигателя постоянного тока, приводящего в действие инерционную нагрузку, показывает угловую скорость нагрузки, $λ (t$ ), в качестве выходного сигнала и приложенного напряжения, $_{} в$ качестве входного сигнала. Конечной целью этого примера является управление угловой скоростью путем изменения приложенного напряжения. На этом рисунке показана простая модель двигателя постоянного тока.

Простая модель двигателя постоянного тока, приводящего в действие инерционную нагрузку

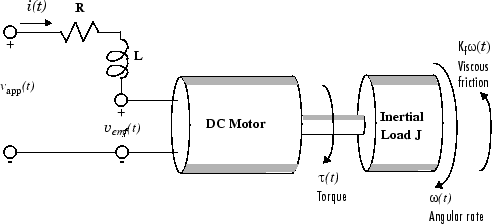
В этой модели идеализируется динамика самого мотора; например, предполагается, что магнитное поле является постоянным. Сопротивление цепи обозначается R, а самоиндуктивность якоря - L. Если вы не знакомы с основами моделирования двигателей постоянного тока, обратитесь к любому базовому тексту по физическому моделированию. С помощью этой простой модели и основных законов физики можно разработать дифференциальные уравнения, описывающие поведение этой электромеханической системы. В этом примере взаимосвязи между электрическим потенциалом и механической силой являются законом индукции Фарадея и законом Ампера для силы на проводнике, движущемся через магнитное поле.

Математическая деривация

Крутящий момент, наблюдаемый на валу двигателя, пропорционален току i, индуцированному приложенным напряжением,

$start(t)_{=} Kmi$ (t)

где _Km, постоянная якоря, связана с физическими свойствами двигателя, такими как напряженность магнитного поля, количество витков провода вокруг катушки проводника и так далее. Обратная (индуцированная) электродвижущая сила, $_{startemf}$ , представляет собой напряжение, пропорциональное угловой скорости $λ$ , наблюдаемой на валу,

$_{startemf} (t)_{=} Кбом$ (t)

где _Kb, постоянная ЭДС, также зависит от определенных физических свойств двигателя.

Механическая часть уравнений двигателя выводится с помощью закона Ньютона, который утверждает, что инерционная нагрузка J, умноженная на производную угловой скорости, равна сумме всех моментов вокруг вала двигателя. Результатом является это уравнение,

$\frac{}{}_{}_{} Jdwdt=∑τi=−Kfω (t)_{+} Kmi$ (t)

где $_{} Kfλ$ - линейная аппроксимация для вязкого трения.

Наконец, электрическая часть уравнений двигателя может быть описана

$_{(t)}_{− (} t) \frac{}{=} Ldidt$ + Ri (t)

или, решение для приложенного напряжения и замена для задней emf,

$_{startapp} (t) \frac{=}{} Ldidt + {Ri}_{} (t)$ + Кбом (t)

Эта последовательность уравнений приводит к набору из двух дифференциальных уравнений, которые описывают поведение двигателя, первое для индуцированного тока,

$\frac{}{didt} = \frac{}{-} RLi \frac{(_{t}}{)} - \frac{}{KbLλ}_{(t)} +$ 1Lstartapp (t)

и второй для результирующей угловой скорости,

$\frac{}{dü dt} = \frac{}{-}_{} 1JKfλ \frac{(}{t})_{} +$ 1JKmi (t)

Уравнения состояния и пространства для двигателя постоянного тока

Учитывая два дифференциальных уравнения, полученные в последнем разделе, теперь можно разработать представление состояния-пространства двигателя постоянного тока как динамической системы. Ток i и угловая скорость λ являются двумя состояниями системы. Прикладываемое напряжение $_{-}$ это входное напряжение системы, а угловая скорость λ - это выходное напряжение.

$\frac{}{} \begin{matrix} \end{matrix} \begin{matrix} \frac{}{} & \frac{_{}}{} \\ \frac{_{}}{} & \frac{_{}}{} \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} \frac{}{} \end{matrix}_{ddt[iω]=[−RL−KbLKmJ−KfJ]⋅[iω]+[1L0]⋅υapp} (t$ )

Пример представления состояния и пространства двигателя постоянного тока

$y (t) \begin{matrix} \end{matrix} \begin{matrix} \end{matrix}_{} =[01]⋅[iω]+[0]⋅υapp$ (t)

Построение моделей SISO

После разработки набора дифференциальных уравнений, описывающих растение, можно создавать модели SISO с помощью простых команд. В следующих разделах рассматриваются

Построение модели состояния и пространства двигателя постоянного тока
Преобразование между представлениями модели
Создание передаточной функции и моделей нулевого/полюсного/усиления

Построение модели состояния и пространства двигателя постоянного тока

Введите следующие номинальные значения для различных параметров двигателя постоянного тока.

R= 2.0 % Ohms
L= 0.5 % Henrys
Km = .015 % torque constant
Kb = .015 % emf constant
Kf = 0.2 % Nms
J= 0.02 % kg.m^2

Учитывая эти значения, можно построить числовое представление состояния-пространства с помощью ss функция.

A = [-R/L -Kb/L; Km/J -Kf/J]
B = [1/L; 0];
C = [0 1];
D = [0];
sys_dc = ss(A,B,C,D)

Эти команды возвращают следующий результат:

a = 
                        x1           x2
           x1           -4        -0.03
           x2         0.75          -10
 
 
b = 
                        u1
           x1            2
           x2            0
 
 
c = 
                        x1           x2
           y1            0            1
 
 
d = 
                        u1
           y1            0

Преобразование между представлениями модели

Теперь, когда имеется представление состояния-пространства двигателя постоянного тока, можно преобразовать в другие представления модели, включая модели передаточной функции (TF) и нулевого/полюсного/усиления (ZPK).

Представление передаточной функции. Вы можете использовать tf для преобразования из представления состояния-пространства в передаточную функцию. Например, этот код используется для преобразования в представление передаточной функции двигателя постоянного тока.

sys_tf = tf(sys_dc)

Transfer function:
       1.5
------------------
s^2 + 14 s + 40.02

Представление нуля/полюса/усиления. Аналогично, zpk функция преобразует из представлений state-space или transfer function в формат нуля/полюса/усиления. Этот код используется для преобразования представления состояния-пространства в форму нуля/полюса/усиления для двигателя постоянного тока.

sys_zpk = zpk(sys_dc)
 
Zero/pole/gain:
        1.5
-------------------
(s+4.004) (s+9.996)

Примечание

Представление состояния-пространства лучше всего подходит для числовых вычислений. Для наивысшей точности преобразуйте в пространство состояния перед объединением моделей и избегайте представления передаточной функции и нулевого/полюсного/усиления, за исключением спецификации модели и проверки.

Построение передаточной функции и моделей нуля/полюса/усиления

В примере двигателя постоянного тока подход «состояние-пространство» создает набор матриц, который представляет модель. При выборе другого подхода можно построить соответствующие модели с помощью tf, zpk, ss, или frd.

sys = tf(num,den)               % Transfer function
sys = zpk(z,p,k)                % Zero/pole/gain
sys = ss(a,b,c,d)               % State-space
sys = frd(response,frequencies) % Frequency response data

Например, можно создать передаточную функцию, указав числитель и знаменатель с помощью этого кода.

sys_tf = tf(1.5,[1 14 40.02])
 
Transfer function:
       1.5
------------------
s^2 + 14 s + 40.02

Кроме того, если требуется создать передаточную функцию двигателя постоянного тока напрямую, используйте эти команды.

s = tf('s');
sys_tf = 1.5/(s^2+14*s+40.02)

Эти команды приводят к выполнению этой функции передачи.

Transfer function:
        1.5
--------------------
s^2 + 14 s + 40.02

Для построения модели нуля/полюса/усиления используйте эту команду.

sys_zpk = zpk([],[-9.996 -4.004], 1.5)

Эта команда возвращает следующее представление нуля/полюса/усиления.

Zero/pole/gain:
        1.5
-------------------
(s+9.996) (s+4.004)

Создание дискретных временных систем

Программное обеспечение Control System Toolbox обеспечивает полную поддержку систем дискретного времени. Дискретные системы можно создавать так же, как и аналоговые системы; единственное отличие состоит в том, что необходимо указать период времени образца для любой создаваемой модели. Например,

sys_disc = tf(1, [1 1], .01);

создает модель SISO в формате передаточной функции.

Transfer function:
  1
-----
z + 1
 
Sample time: 0.01

Добавление временных задержек к дискретным временным моделям

Можно добавить временные задержки в модели дискретного времени, указав задержку ввода, задержку вывода или задержку ввода-вывода при построении модели. Временная задержка должна быть неотрицательным целым числом, которое представляет кратное времени выборки. Например,

sys_delay = tf(1, [1 1], 0.01,'ioDelay',5)

возвращает систему с задержкой ввода-вывода 5 с.

Transfer function:
           1
z^(-5) * -----
         z + 1
 
Sample time: 0.01

Добавление задержек в линейные модели

Можно добавить временные задержки в линейные модели, указав задержку ввода, задержку вывода или задержку ввода-вывода при построении модели. Например, чтобы добавить задержку ввода-вывода к двигателю постоянного тока, используйте этот код.

sys_tfdelay = tf(1.5,[1 14 40.02],'ioDelay',0.05)

Эта команда создает функцию передачи двигателя постоянного тока, но добавляет задержку 0,05 секунды.

Transfer function:
                      1.5
exp(-0.05*s) * ------------------
               s^2 + 14 s + 40.02

Дополнительные сведения о добавлении временных задержек в модели см. в разделе Временные задержки в линейных системах.

Объекты LTI

Для удобства программа Control System Toolbox использует пользовательские структуры данных, называемые объектами LTI, для хранения данных, связанных с моделью. Например, переменная sys_dc созданный для примера двигателя постоянного тока называется объектом SS. Существуют также объекты TF, ZPK и FRD для моделей передаточной функции, нулевого/полюсного/усиления и частотного отклика данных соответственно. Четыре объекта LTI инкапсулируют данные модели и позволяют манипулировать линейными системами как отдельными объектами, а не как коллекциями векторов или матриц.

Чтобы увидеть, что содержат объекты LTI, используйте get команда. Этот код описывает содержимое sys_dc из примера двигателя постоянного тока.

get(sys_dc)
                A: [2×2 double]
                B: [2×1 double]
                C: [0 1]
                D: 0
                E: []
           Scaled: 0
        StateName: {2×1 cell}
        StateUnit: {2×1 cell}
    InternalDelay: [0×1 double]
       InputDelay: 0
      OutputDelay: 0
               Ts: 0
         TimeUnit: 'seconds'
        InputName: {''}
        InputUnit: {''}
       InputGroup: [1×1 struct]
       OutputName: {''}
       OutputUnit: {''}
      OutputGroup: [1×1 struct]
            Notes: [0×1 string]
         UserData: []
             Name: ''
     SamplingGrid: [1×1 struct]

Управлять данными, содержащимися в объектах LTI, можно с помощью set команда; см. справочные страницы панели инструментов системы управления для описания set и get.

Другим удобным способом установки или извлечения свойств модели LTI является прямой доступ к ним с помощью точечной нотации. Например, если требуется получить доступ к значению A матрица, вместо использования get, можно ввести

sys_dc.A

в подсказке MATLAB ®. Эта нотация возвращает A матрица.

ans =

   -4.0000   -0.0300
    0.7500  -10.0000

Аналогично, если требуется изменить значения A матрица, вы можете сделать это напрямую, как показывает этот код.

A_new = [-4.5 -0.05; 0.8 -12.0];
sys_dc.A = A_new;

См. также

ss | tf | zpk

Связанные примеры

Подробнее

Числовые модели

Документация