Документация

Создание выборочной системы с разомкнутым контуром с выходной задержкой.

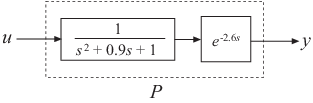
s = tf('s');
P = exp(-2.6*s)/(s^2+0.9*s+1);

P является функцией переноса второго заказа (tf) объект с временной задержкой.

Вычислить аппроксимацию Паде первого порядка P.

Pnd1 = pade(P,1)

Pnd1 =
 
             -s + 0.7692
  ----------------------------------
  s^3 + 1.669 s^2 + 1.692 s + 0.7692
 
Continuous-time transfer function.

Эта команда заменяет все временные задержки в P с приближением первого порядка. Поэтому Pnd1 является функцией переноса третьего заказа без задержек.

Сравнение частотной характеристики исходной и приблизительной моделей с помощью bodeplot.

h = bodeoptions;
h.PhaseMatching = 'on';
bodeplot(P,'-b',Pnd1,'-.r',{0.1,10},h)
legend('Exact delay','First-Order Pade','Location','SouthWest')

Величина P и Pnd1 точно совпадать. Однако этап Pnd1 отклоняется от фазы P за пределами приблизительно 1 рад/с.

Увеличение порядка аппроксимации Паде для расширения полосы частот, в которой аппроксимация фазы является хорошей.

Pnd3 = pade(P,3);

Сравните частотную характеристику P, Pnd1 и Pnd3.

bodeplot(P,'-b',Pnd3,'-.r',Pnd1,':k',{0.1 10},h)
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','SouthWest')

Погрешность аппроксимации фазы уменьшается с помощью аппроксимации Паде третьего порядка.

Сравнение ответов во временной области исходной и приближенной систем с помощью stepplot.

stepplot(P,'-b',Pnd3,'-.r',Pnd1,':k')
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','Southeast')

Использование аппроксимации Паде вводит неминумный артефакт фазы (эффект «неправильного пути») в начальный переходный отклик. Эффект достаточно выражен в приближении первого порядка, которое перед изменением направления опускается значительно ниже нуля. Эффект уменьшается в аппроксимации более высокого порядка, которая намного ближе соответствует точной реакции системы.