Документация

Интерполяция кубических сплайнов данных сглаживания

Предположим, что требуется интерполяция некоторых гладких данных, например, для

rng(6), x = (4*pi)*[0 1 rand(1,15)]; y = sin(x);

Можно использовать интерполятор кубического сплайна, полученный

cs = csapi(x,y);

и постройте график сплайна вместе с данными со следующим кодом:

fnplt(cs);
hold on
plot(x,y,'o')
legend('cubic spline','data')
hold off

В результате получается цифра, подобная следующей.

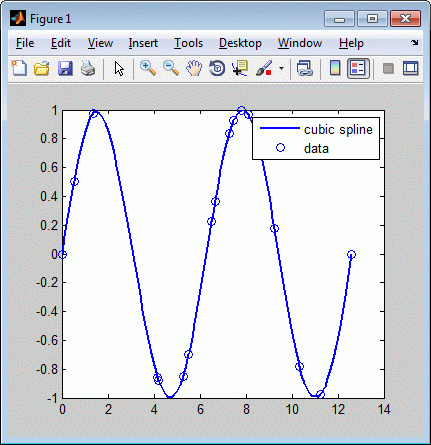
Это, точнее, кубический сплайн-интерполятор с не-а-узел концевыми условиями, что означает, что это уникальный кусочно-кубический многочлен с двумя непрерывными производными с разрывами на всех внутренних участках данных, кроме крайнего левого и крайнего правого. Это тот же интерполятор, что и в MATLAB ®spline команда, spline(x,y).

Периодические данные

Синусоидальная функция является 2δ-периодической. Чтобы проверить, насколько хорошо ваш интерполятор работает с этой оценкой, вычислите, например, разницу в значении его первой производной в двух конечных точках,

diff(fnval(fnder(cs),[0 4*pi]))
ans = -.0100

что не так хорошо. Если вы предпочитаете получить интерполятор, первая и вторая производные которого находятся в двух конечных точках, 0 и 4*pi, сопоставить, использовать вместо команды csape что позволяет определять множество различных типов конечных условий, включая периодические конечные условия. Итак, используйте вместо

pcs = csape(x,y,'periodic');

за что и получаешь

diff(fnval(fnder(pcs),[0 4*pi]))

Вывод: ans = 0 как разность конечных откосов. Даже разница в конечных вторых производных невелика:

diff(fnval(fnder(pcs,2),[0 4*pi]))

Вывод: ans = -4.6074e-015.

Другие конечные условия

Также могут быть обработаны и другие конечные условия. Например,

cs = csape(x,[3,y,-4],[1 2]);

обеспечивает интерполяцию кубического сплайна с разрывами на и с наклоном на крайнем левом участке данных, равным 3, и его второй производной на крайнем правом участке данных, равным -4.

Общая интерполяция сплайнов

Если требуется интерполяция на площадках, отличных от разрывов и/или сплайнов, отличных от кубических сплайнов, с помощью простых узлов, то используется spapi команда. В самом простом виде, вы бы сказали sp = spapi(k,x,y); в котором первый аргумент, k, задает порядок интерполяции сплайна; это число коэффициентов в каждой части многочлена, т.е. на 1 больше номинальной степени ее частей многочлена. Например, на следующем рисунке показан линейный, квадратичный и квадратичный сплайн, интерполированный с данными, полученными с помощью операторов

sp2 = spapi(2,x,y); fnplt(sp2,2), hold on
sp3 = spapi(3,x,y); fnplt(sp3,2,'k--'), 
sp5 = spapi(5,x,y); fnplt(sp5,2,'r-.'), plot(x,y,'o')
legend('linear','quadratic','quartic','data'), hold off

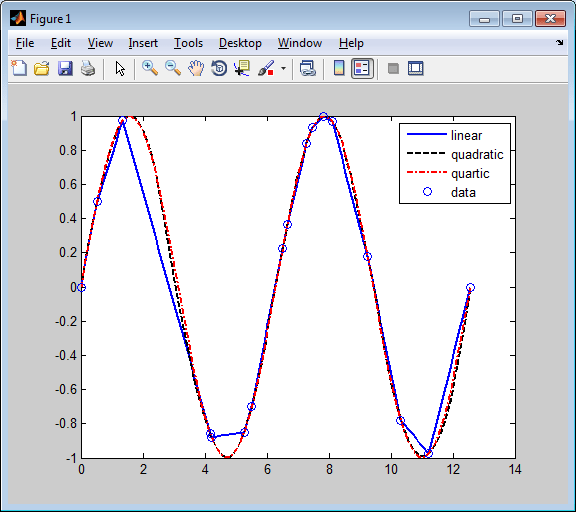
Даже кубический сплайновый интерполятор, полученный из spapi отличается от той, которая предоставляется csapi и spline. Чтобы подчеркнуть их разницу, вычислите и постройте график их вторых производных следующим образом:

fnplt(fnder(spapi(4,x,y),2)), hold on,
fnplt(fnder(csapi(x,y),2),2,'k--'),plot(x,zeros(size(x)),'o')
legend('from spapi','from csapi','data sites'), hold off

Это дает следующий график:

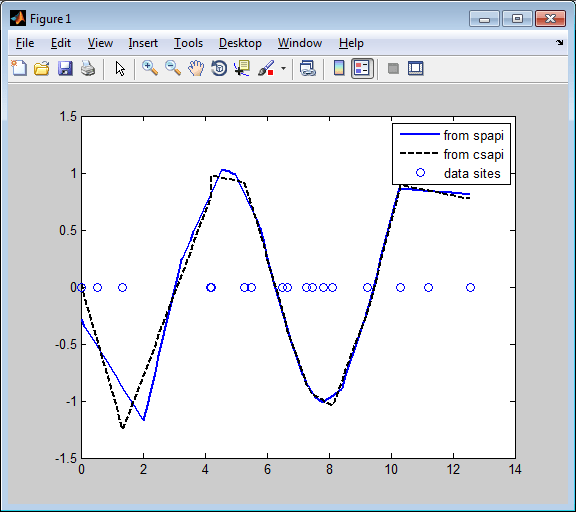
Так как вторая производная кубического сплайна является пунктирной линией, с вершинами в разрывах сплайна можно ясно видеть, что csapi места разрывы на сайтах данных, в то время как spapi не делает.

Узловые варианты

Фактически, можно явно указать, где должен быть разрыв сплайнового интерполятора, с помощью команды sp = spapi(knots,x,y); в которой последовательность knots поставляет определенным образом используемые разрывы. Например, вспоминая, что вы выбрали y быть sin(x), команда

ch = spapi(augknt(x,4,2),[x x],[y cos(x)]);

обеспечивает кубический интерполятор Эрмита для синусоидальной функции, а именно кусочно-кубической функции, с разрывами на всех x(i)'s, что соответствует синусоидальной функции по значению и наклону на всех x(i)Это делает интерполятор непрерывным с непрерывной первой производной, но, в общем, он имеет прыжки через разрывы в своей второй производной. Как эта команда может узнать, какая часть массива значений данных [y cos(x)] предоставляет значения и какие уклоны? Обратите внимание, что массив сайта данных здесь указан как [x x], т.е. каждый узел данных появляется дважды. Также обратите внимание, что y(i) связано с первым вхождением x(i), и cos(x(i)) связано со вторым вхождением x(i). Значение данных, связанное с первым появлением узла данных, принимают за значение функции; значение данных, связанное со вторым внешним видом, принимается за наклон. Если бы был третий вид этого сайта данных, соответствующее значение данных принималось бы в качестве второго значения производной, которое должно совпадать на этом сайте. Описание команды см. в разделе Построение и работа со сплайнами B-формы augknt используется здесь для генерации соответствующей «узловой последовательности».

Сглаживание

Что если данные шумят? Например, предположим, что заданные значения

noisy = y + .3*(rand(size(x))-.5);

Тогда вы можете предпочесть аппроксимацию. Например, можно попробовать кубический сглаживающий сплайн, полученный командой

scs = csaps(x,noisy);

и нанесено на график

fnplt(scs,2), hold on, plot(x,noisy,'o'),
legend('smoothing spline','noisy data'), hold off

Это приводит к такой цифре:

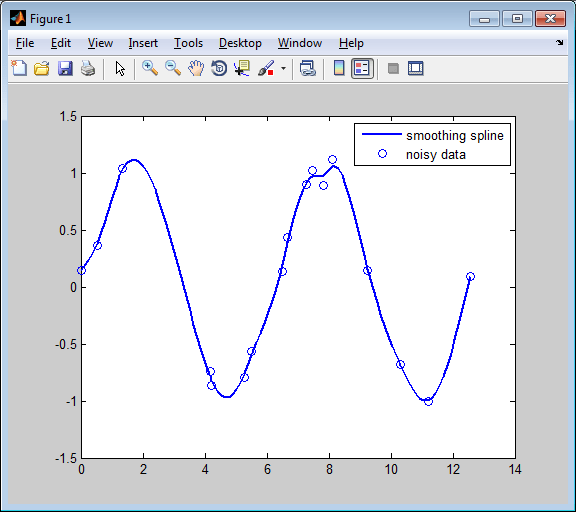
Если вам не нравится уровень сглаживания, сделанный csaps(x,y), вы можете изменить его, указав параметр сглаживания, p, в качестве необязательного третьего аргумента. Выберите это число в диапазоне от 0 до 1. Как p изменяется от 0 до 1, сглаживающий сплайн изменяется, соответственно, от одной крайности, аппроксимации прямой линии наименьших квадратов к данным, до другой крайности, «естественного» кубического сплайна, интерполированного к данным. С тех пор csaps возвращает параметр сглаживания, фактически используемый в качестве дополнительного второго вывода, теперь можно поэкспериментировать следующим образом:

[scs,p] = csaps(x,noisy); fnplt(scs,2), hold on
fnplt(csaps(x,noisy,p/2),2,'k--'), 
fnplt(csaps(x,noisy,(1+p)/2),2,'r:'), plot(x,noisy,'o')
legend('smoothing spline','more smoothed','less smoothed',...
'noisy data'), hold off

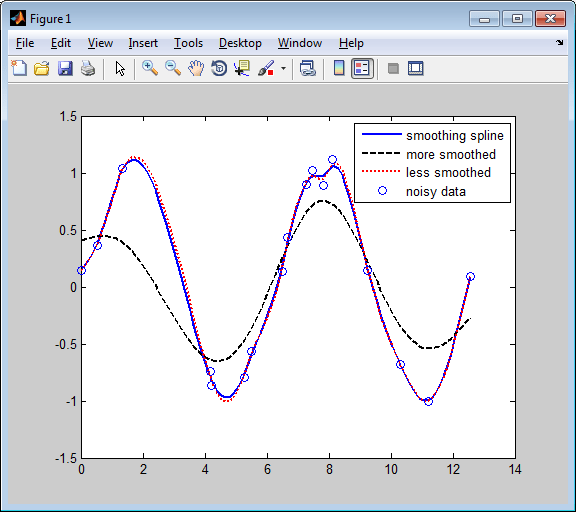
В результате получается следующее изображение.

Иногда можно просто получить самый гладкий кубический сплайн. sp который находится в пределах заданного допуска tol данных в том смысле, что norm(noisy - fnval(sp,x))^2 <= tol. Этот сплайн создается с помощью команды sp = spaps(x,noisy,tol) для определенного допуска tol.

Наименьшие квадраты

Если вы предпочитаете аппроксиматор наименьших квадратов, вы можете получить его с помощью оператора sp = spap2(knots,k,x,y); в котором обе последовательности узлов knots и заказ k сплайна.

Популярный выбор для порядка 4, и это дает вам кубический сплайн. Если у вас нет четкого представления о том, как выбрать узлы, просто укажите количество полиномиальных частей, которые вы хотите использовать. Например,

sp = spap2(3,4,x,y); 

дает кубический сплайн, состоящий из трех отрезков полинома. Если результирующая ошибка неравномерна, вы можете попытаться улучшить распределение узлов, используя newknt следующим образом:

sp = spap2(newknt(sp),4,x,y);