Моделирование коэффициентов регрессии и дисперсии возмущений байесовской модели линейной регрессии
[ возвращает случайный вектор коэффициентов регрессии (BetaSim,sigma2Sim] = simulate(Mdl)BetaSim) и случайную дисперсию возмущений (sigma2Sim) из байесовской модели линейной регрессии
Mdl из β и start2.
[ извлекает из краевых задних распределений, полученных или обновленных путем включения данных предиктора BetaSim,sigma2Sim] = simulate(Mdl,X,y)X и соответствующие данные ответа y.
Если Mdl является совместной предшествующей моделью, то simulate создает краевые апостериорные распределения путем обновления предшествующей модели информацией о параметрах, которые она получает из данных.
Если Mdl является краевой задней моделью, то simulate обновляет апостериоры информацией о параметрах, которые они получают из дополнительных данных. Полная вероятность данных состоит из дополнительных данных. X и yи данные, которые были созданы Mdl.
NaNs в данных указывают отсутствующие значения, которые simulate удаляет, используя удаление по списку.
[ использует любую из комбинаций входных аргументов в предыдущих синтаксисах и дополнительных параметрах, заданных одним или несколькими аргументами пары имя-значение. Например, для моделирования из условного апостериорного распределения одного параметра можно задать значение β или start2, учитывая заданное значение другого параметра.BetaSim,sigma2Sim] = simulate(___,Name,Value)
[ также возвращает данные из распределения скрытого режима, если BetaSim,sigma2Sim,RegimeSim] = simulate(___)Mdl - байесовская модель линейной регрессии для стохастического выбора переменных поиска (SSVS), то есть, если Mdl является mixconjugateblm или mixsemiconjugateblm объект модели.
simulate не может извлекать значения из неправильного распределения, то есть распределения, плотность которого не интегрируется в 1.
Если Mdl является empiricalblm объект модели, то вы не можете указать Beta или Sigma2. Нельзя моделировать из условных задних распределений с помощью эмпирического распределения.
Каждый раз, когда simulate должен оценить апостериорное распределение (например, когда Mdl представляет собой предыдущее распределение, и вы поставляете X и y) и задняя является аналитически отслеживаемой, simulate моделируется непосредственно с задней стороны. В противном случае simulate прибегает к моделированию Монте-Карло для оценки заднего. Дополнительные сведения см. в разделе Апостериорная оценка и вывод.
Если Mdl является задней моделью сустава, то simulate моделирует данные из него по-разному по сравнению с Mdl является совместной предыдущей моделью, и вы поставляете X и y. Таким образом, если задать одно и то же случайное начальное число и создать случайные значения обоими способами, то могут не быть получены одинаковые значения. Однако соответствующие эмпирические распределения, основанные на достаточном количестве розыгрышей, фактически эквивалентны.
На этом рисунке показано, как simulate уменьшает выборку, используя значения NumDraws, Thin, и BurnIn.
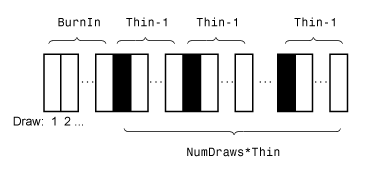
Прямоугольники представляют последовательные розыгрыши из распределения. simulate удаляет белые прямоугольники из образца. Остающееся NumDraws образец составляют черные прямоугольники.
Если Mdl является semiconjugateblm объект модели, затем simulate образцы из заднего распределения путем применения образца Гиббса.
simulate использует значение по умолчанию Sigma2Start для start2 и рисует значение β из λ (β 'start2, X, y).
simulate рисует значение, равное λ 2, из δ2 | β, X, y), используя ранее сгенерированное значение β.
Функция повторяет шаги 1 и 2 до сходимости. Чтобы оценить сходимость, нарисуйте график трассировки образца.
При указании BetaStart, то simulate вычерчивает значение, равное start2, из δ (start2 | β, X, y), чтобы запустить пробоотборник Гиббса.simulate не возвращает это генерируемое значение, равное
Если Mdl является empiricalblm объект модели и вы не поставляете X и y, то simulate рисует из Mdl.BetaDraws и Mdl.Sigma2Draws. Если NumDraws меньше или равно numel(Mdl.Sigma2Draws), то simulate возвращает первое NumDraws элементы Mdl.BetaDraws и Mdl.Sigma2Draws в виде случайных розыгрышей для соответствующего параметра. В противном случае simulate случайные повторные выборки NumDraws элементы из Mdl.BetaDraws и Mdl.Sigma2Draws.
Если Mdl является customblm объект модели, затем simulate использует пробоотборник MCMC для извлечения из заднего распределения. При каждой итерации программное обеспечение объединяет текущие значения коэффициентов регрессии и дисперсии возмущений в (Mdl.Intercept + Mdl.NumPredictors + 1) -by-1 вектор и передает его вMdl.LogPDF. Значение дисперсии возмущений является последним элементом этого вектора.
Пробоотборник HMC требует как логарифмической плотности, так и его градиента. Градиент должен быть (NumPredictors+Intercept+1)вектор -by-1. Если производные определенных параметров трудно вычислить, то в соответствующих местах градиента подать NaN вместо этого значения. simulate заменяет NaN значения с числовыми производными.
Если Mdl является lassoblm, mixconjugateblm, или mixsemiconjugateblm объект модели и поставка X и y, то simulate образцы из заднего распределения путем применения образца Гиббса. Если данные не предоставляются, то simulate образцы из аналитических, безусловных предыдущих распределений.
simulate не возвращает созданные по умолчанию начальные значения.
Если Mdl является mixconjugateblm или mixsemiconjugateblm, то simulate сначала извлекает из распределения режима, учитывая текущее состояние цепочки (значения RegimeStart, BetaStart, и Sigma2Start). Если нарисовать один образец и не указывать значения для RegimeStart, BetaStart, и Sigma2Start, то simulate использует значения по умолчанию и выдает предупреждение.
conjugateblm | customblm | diffuseblm | empiricalblm | lassoblm | mixconjugateblm | mixsemiconjugateblm | semiconjugateblm