В этом примере показано, как использовать два различных метода для калибровки модели стохастической волатильности SABR из рыночных подразумеваемых волатильностей черного. Использование обоих подходов blackvolbysabr.
В этом примере показано, как настроить гипотетический рынок, подразумевающий волатильность черного для европейских свопционов в диапазоне ударов перед калибровкой. Свопции истекают через три года с Settle дата и иметь 10-летние свопы в качестве базового инструмента. Ставки выражаются в десятичных разрядах. (Изменение единиц измерения влияет на числовое значение и интерпретацию Alpha входной параметр для функции blackvolbysabr.)
Загрузка рынка подразумевала данные о волатильности черного для свопционов, истекающих через три года.
Settle = '12-Jun-2013'; ExerciseDate = '12-Jun-2016'; MarketStrikes = [2.0 2.5 3.0 3.5 4.0 4.5 5.0]'/100; MarketVolatilities = [45.6 41.6 37.9 36.6 37.8 39.2 40.0]'/100;
На момент Settle, определить базовую форвардную ставку и волатильность по цене.
CurrentForwardValue = MarketStrikes(4) ATMVolatility = MarketVolatilities(4)
CurrentForwardValue =
0.0350
ATMVolatility =
0.3660В этом примере показано, как откалибровать Alpha, Rho, и Nu непосредственно входные параметры. Значение Beta предопределяется либо путем подбора исторических данных о волатильности рынка, либо путем выбора стоимости, которая считается подходящей для этого рынка [1].
Определение заранее определенного Beta.
Beta1 = 0.5;
После фиксации значения (Beta), параметры (Alpha), ρ (Rho), иNu) все устанавливаются непосредственно. Функция Toolbox™ оптимизации lsqnonlin генерирует значения параметров, которые минимизируют квадрат ошибки между волатильностью рынка и волатильностью, вычисленной blackvolbysabr.
% Calibrate Alpha, Rho, and Nu objFun = @(X) MarketVolatilities - ... blackvolbysabr(X(1), Beta1, X(2), X(3), Settle, ... ExerciseDate, CurrentForwardValue, MarketStrikes); X = lsqnonlin(objFun, [0.5 0 0.5], [0 -1 0], [Inf 1 Inf]); Alpha1 = X(1); Rho1 = X(2); Nu1 = X(3);
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the default value of the function tolerance.
В этом примере показано, как использовать альтернативный метод калибровки, где значение (Beta) снова предопределяется, как в способе 1.
Определение заранее определенного Beta.
Beta2 = 0.5;
Однако после фиксации значения (Beta), параметры (Rho), иNu) устанавливаются непосредственно при (Alpha) подразумевается из волатильности рынка в деньгах. Модели, откалиброванные с помощью этого метода, производят волатильность по цене, равную рыночным котировкам. Этот подход широко используется в свопционах, где волатильность по отношению к деньгам котируется чаще всего и имеет важное значение для сопоставления. Чтобы подразумевать (Alpha) от волатильности рынка в деньгах (« решается следующий кубический многочлен (Alpha), и выбирается наименьший положительный реальный корень [2].
3ρ224υ2T) α − startATMF (1 − β) = 0
где:
- текущее прямое значение.
- доля года до погашения.
Для этого определите анонимную функцию как:
% Year fraction from Settle to option maturity T = yearfrac(Settle, ExerciseDate, 1); % This function solves the SABR at-the-money volatility equation as a % polynomial of Alpha alpharoots = @(Rho,Nu) roots([... (1 - Beta2)^2*T/24/CurrentForwardValue^(2 - 2*Beta2) ... Rho*Beta2*Nu*T/4/CurrentForwardValue^(1 - Beta2) ... (1 + (2 - 3*Rho^2)*Nu^2*T/24) ... -ATMVolatility*CurrentForwardValue^(1 - Beta2)]); % This function converts at-the-money volatility into Alpha by picking the % smallest positive real root atmVol2SabrAlpha = @(Rho,Nu) min(real(arrayfun(@(x) ... x*(x>0) + realmax*(x<0 || abs(imag(x))>1e-6), alpharoots(Rho,Nu))));
Функция atmVol2SabrAlpha преобразует волатильность в деньгах в (Alpha) для заданного набора, равного (Rho) иNu). Эта функция затем используется в целевой функции, чтобы подогнать параметры (Rho) иNu).
% Calibrate Rho and Nu (while converting at-the-money volatility into Alpha % using atmVol2SabrAlpha) objFun = @(X) MarketVolatilities - ... blackvolbysabr(atmVol2SabrAlpha(X(1), X(2)), ... Beta2, X(1), X(2), Settle, ExerciseDate, CurrentForwardValue, ... MarketStrikes); X = lsqnonlin(objFun, [0 0.5], [-1 0], [1 Inf]); Rho2 = X(1); Nu2 = X(2);
Local minimum found. Optimization completed because the size of the gradient is less than the default value of the function tolerance.
Калиброванный параметр (Alpha) вычисляется с использованием калиброванных параметровRho) иNu).
% Obtain final Alpha from at-the-money volatility using calibrated parameters Alpha2 = atmVol2SabrAlpha(Rho2, Nu2); % Display calibrated parameters C = {Alpha1 Beta1 Rho1 Nu1;Alpha2 Beta2 Rho2 Nu2}; CalibratedPrameters = cell2table(C,... 'VariableNames',{'Alpha' 'Beta' 'Rho' 'Nu'},... 'RowNames',{'Method 1';'Method 2'})
CalibratedPrameters =
Alpha Beta Rho Nu
________ ____ _______ _______
Method 1 0.060277 0.5 0.2097 0.75091
Method 2 0.058484 0.5 0.20568 0.79647
В этом примере показано, как использовать калиброванные модели для вычисления новых волатильностей при любом значении страйка.
Вычислите летучесть для моделей, откалиброванных с использованием метода 1 и метода 2, и постройте график результатов.
PlottingStrikes = (1.75:0.1:5.50)'/100; % Compute volatilities for model calibrated by Method 1 ComputedVols1 = blackvolbysabr(Alpha1, Beta1, Rho1, Nu1, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); % Compute volatilities for model calibrated by Method 2 ComputedVols2 = blackvolbysabr(Alpha2, Beta2, Rho2, Nu2, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); figure; plot(MarketStrikes,MarketVolatilities,'xk',... PlottingStrikes,ComputedVols1,'b', ... PlottingStrikes,ComputedVols2,'r', ... CurrentForwardValue,ATMVolatility,'ok',... 'MarkerSize',10); xlim([0.01 0.06]); ylim([0.35 0.5]); xlabel('Strike', 'FontWeight', 'bold'); ylabel('Implied Black Volatility', 'FontWeight', 'bold'); legend('Market Volatilities', 'SABR Model (Method 1)',... 'SABR Model (Method 2)', 'At-the-money volatility');
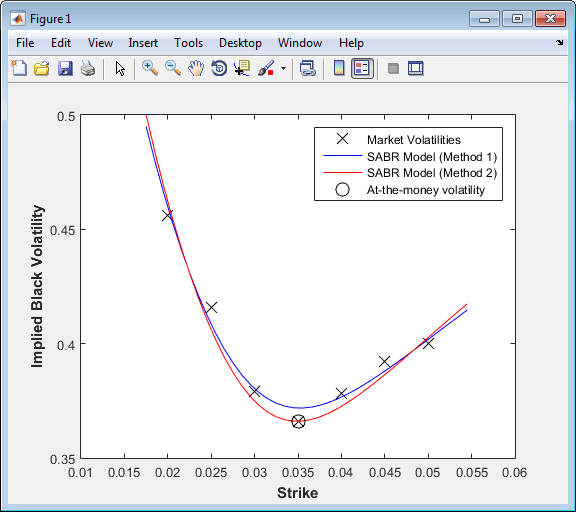
Модель, откалиброванная с помощью метода 2, точно воспроизводит волатильность рынка в деньгах (помечена кругом).
[1] Хаган, П. С., Кумар, Д., Лесневски, А. С. и Вудворд, Д. Э., Управление риском улыбки, журнал Wilmott, 2002.
[2] West, G., «Калибровка модели SABR на неликвидных рынках», Applied Mathematical Finance, 12 (4), pp. 371-385, 2004.
blackvolbysabr | optsensbysabr | swaptionbyblk