До сих пор не разработано более формальное определение «урожайности» и ее применения. Во многих ситуациях, когда денежный поток доступен, факторы дисконтирования денежных потоков могут быть не сразу очевидны. В других случаях релевантным часто является разброс, разница между кривыми (также известная как термин структура разброса).
Все эти расчеты требуют одного основного компонента - казначейского спота, номинальной доходности или форвардной кривой. Как правило, генерация этих кривых начинается с ряда текущих и выбранных внеоборотных проблем в качестве входных данных.
Программное обеспечение MATLAB ® использует эти облигации для поиска спотовых ставок по одному, начиная с самого короткого срока, используя методы начальной загрузки. Все денежные потоки используются для построения спотовой кривой, а ставки между сроками погашения (для этих купонов) интерполируются линейно .
Для иллюстрации того, как это работает, наблюдайте использование zbtyield (или эквивалентно zbtprice) по портфелю из шести казначейских векселей и облигаций.
Счета | Дата погашения | Текущая доходность |
|---|---|---|
3 месяца | 4/17/03 | 1.15 |
6 месяцев | 7/17/03 | 1.18 |
| Ноты/Облигации | Купон | Дата погашения | Текущая доходность |
|---|---|---|---|
2 года | 1.750 | 12/31/04 | 1.68 |
5 лет | 3.000 | 11/15/07 | 2.97 |
10 лет | 4.000 | 11/15/12 | 4.01 |
30 лет | 5.375 | 2/15/31 | 4.92 |
Для вывода спотовой кривой можно указать цены или доходности указанных выше облигаций. Функция zbtyield принимает выходы (эквивалентный выход облигаций, если быть точным).
Чтобы продолжить, сначала соберите приведенную выше таблицу в переменную с именем Bonds. Первый столбец содержит сроки погашения, второй - купоны, а третий - условные или номинальные значения облигаций. (Обратите внимание, что купоны имеют нулевые купоны.)
Bonds = [datenum('04/17/2003') 0 100; datenum('07/17/2003') 0 100; datenum('12/31/2004') 0.0175 100; datenum('11/15/2007') 0.03 100; datenum('11/15/2012') 0.04 100; datenum('02/15/2031') 0.05375 100];
Затем укажите соответствующие выходы.
Yields = [0.0115;
0.0118;
0.0168;
0.0297;
0.0401;
0.0492];
Теперь вы готовы вычислить спотовую кривую для каждого из этих шести сроков погашения. Спотовая кривая основана на дате расчета 17 января 2003 года.
Settle = datenum('17-Jan-2003');
[ZeroRates, CurveDates] = zbtyield(Bonds, Yields, Settle)
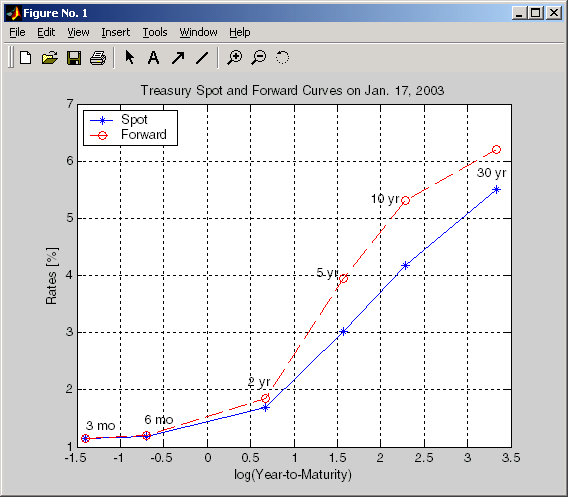
Это дает вам спотовую кривую казначейства за день.
Можно вычислить прямую кривую по этой точечной кривой с помощью zero2fwd.
[ForwardRates, CurveDates] = zero2fwd(ZeroRates, CurveDates, ... Settle)
Здесь понятие форвардных ставок относится к ставкам между указанными выше сроками погашения, а не к определенному периоду (форвардные 3-месячные ставки, например).
Вычисление спреда между определенными фиксированными форвардными периодами (например, спрэд Казначейства-Евродоллара) требует дополнительного шага. Интерполировать нулевые ставки (или нулевые цены, вместо этого) для соответствующих сроков на даты интервала. Затем используйте интерполированные нулевые ставки для вывода форвардных ставок и, таким образом, разброса сегментов форвардной кривой Евродоллара по сравнению с соответствующими форвардными сегментами из казначейских векселей.
Кроме того, разнообразие функций кривой (включая zero2fwd) помогает стандартизировать такие расчеты. Например, при использовании обеих ставок, котируемых с квартальным суммированием и на основе фактических данных/360, полученная структура спреда полностью сопоставима. Это позволяет избежать небольшой несогласованности, которая возникает при прямом сравнении эквивалентной доходности облигаций казначейского векселя с квартальными форвардными ставками, подразумеваемыми фьючерсами на евродоллары.
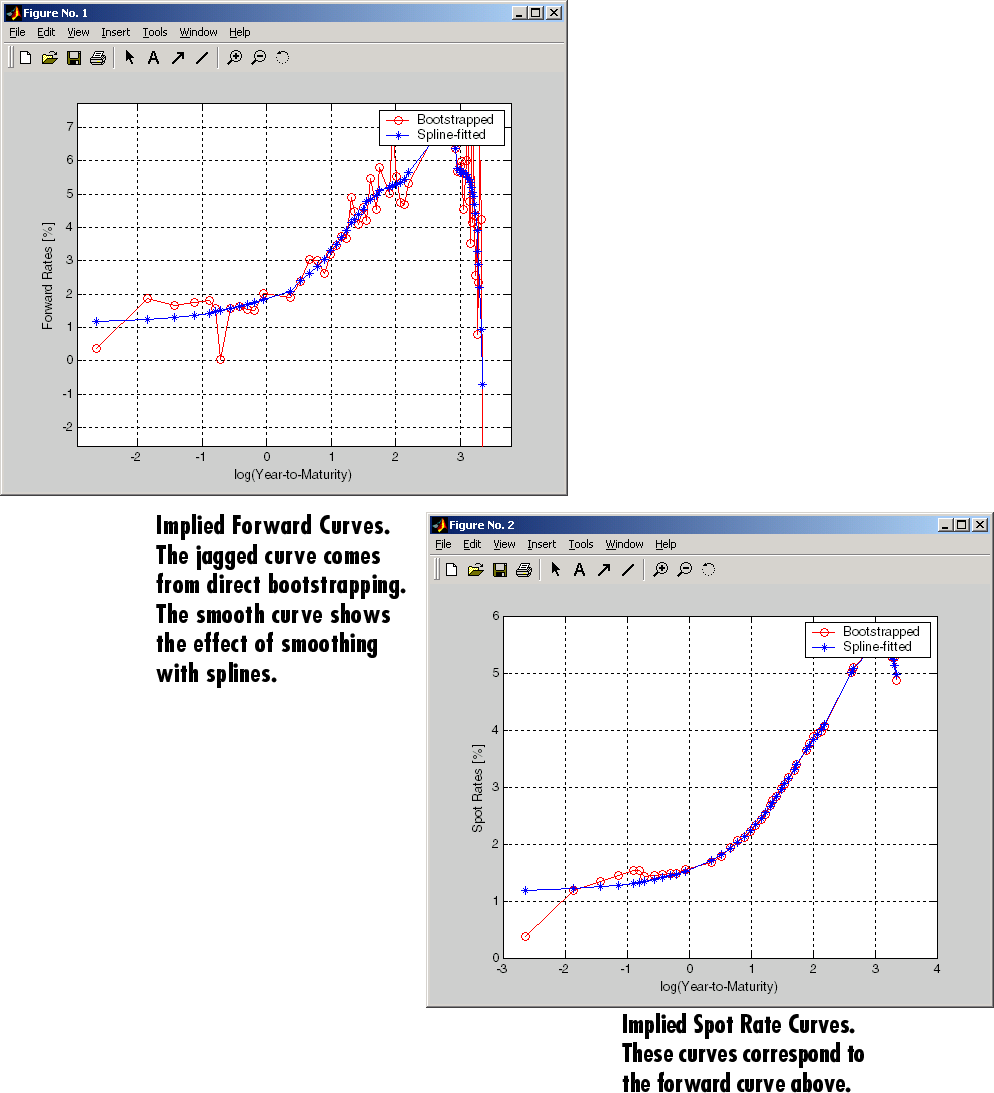
При введении большего количества связей при построении кривых шум может стать фактором и может нуждаться в некотором «сглаживании» (например, со сплайнами); это помогает получить более гладкую прямую кривую.
Следующие спотовые и форвардные кривые построены из 67 казначейских облигаций. Установочная и загрузочная точечная кривая (правый нижний рисунок) показывает сравнимую стабильность. Прямая кривая (верхний левый рисунок) содержит значительный шум и показывает невероятную структуру прямой скорости. Шум не обязательно плохой; он может раскрыть торговые возможности для подхода, основанного на относительной стоимости. Тем не менее, более сбалансированный подход желателен, когда загрузочная прямая кривая колеблется так сильно и содержит отрицательную скорость до -10% (не показана на графике, потому что она находится вне пределов).
В этом примере используется termfit, пример функции из программного обеспечения Financial Toolbox™, которая также требует использования программного обеспечения Curve Fitting Toolbox™.