Financial Instruments Toolbox™ вычисляет цены для Cap, Floor, или Swaption инструмент при моделировании отрицательных процентных ставок с использованием модели нормальной волатильности, сдвинутой модели черного или сдвинутой модели SABR:
Обычная модель волатильности (модель Холостого) для процентных опционов для обработки отрицательных ставок со следующим:
Сдвинутая черная модель и сдвинутая модель SABR для процентных опционов для обработки отрицательных ставок со следующим:
Black объект модели (модель Shilded Black, заданная 'Shift' аргумент «имя-значение» имеет положительное значение.)
Black объект pricer (модель Shilded Black, заданная 'Shift' аргумент «имя-значение» имеет положительное значение.)
SABR объект модели (сдвинутая модель SABR, заданная 'VolatilityType' аргумент «имя-значение» имеет значение "Black" и 'Shift' аргумент «имя-значение» имеет положительное значение.)
SABR pricer object (Сдвинутая модель SABR, заданная 'VolatilityType' аргумент «имя-значение» имеет значение "Black" и 'Shift' аргумент «имя-значение» имеет положительное значение.)
Первоначальные авторы модели SABR предоставили приближенную форму подразумеваемой волатильности черного в терминах параметров модели SABR (известной как «формула Хагана»), чтобы цена опциона могла быть вычислена путем вставки вычисленной волатильности черного SABR в формулу черного:
,
Однако эти методы начали разрушаться с введением отрицательных процентных ставок, из-за предположения черной модели, что базовые ставки логнормально распределены (и поэтому не могут быть отрицательными).
Кроме того, даже когда базовая ставка положительна, известно, что приближенная форма SABR подразумевает волатильность черного (Hagan et al., 2002) становится все более неточной по мере приближения удара к нулю. Даже без пересечения границы нулевого удара подразумеваемая плотность вероятности базовой ставки по истечении опциона может стать отрицательной при низких положительных ударах, хотя плотности вероятности явно не должны быть отрицательными:
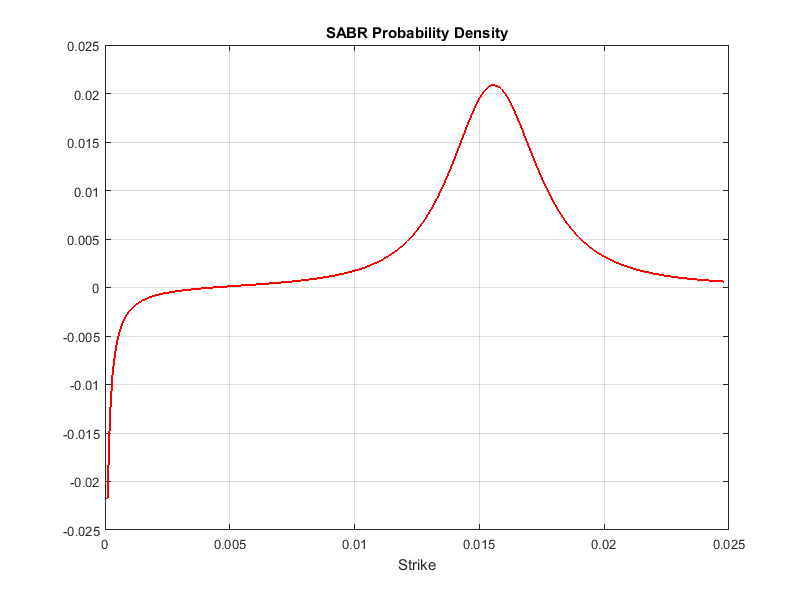
Варианты с негативными ударами не могут быть представлены волатильностью черного. Чтобы обойти эту проблему, рынок начал цитировать цены на кэп, пол и свопцион также с точки зрения нормальных волатильностей или смещенных волатильностей черного. Вместо модели Блэка оба типа волатильности происходят из альтернативных моделей, которые допускают отрицательные ставки.
Нормальные волатильности связаны с моделью Нормаль (также известной как модель Холостяка):
![]()
где предполагается, что базовые скорости нормально распределены. В отличие от логнормальной модели (где скорости имеют нижнюю границу), скорости в модели Normal могут быть как бесконечно положительными, так и бесконечно отрицательными.
Сдвинутые волатильности черного связаны с моделью сдвинутого черного (также известной как модель «смещенной диффузии» или «сдвинутой логнормальной»):
![]()
Модель сдвинутого черного по существу такая же, как модель черного, за исключением того, что она моделирует движения (F + Shift) в качестве базового актива, а не F (где F - форвардная ставка свопа в случае свопционов и форвардная ставка в случае кэплетов и флорлетов). Таким образом, модель сдвинутого черного допускает отрицательные скорости, с фиксированной отрицательной нижней границей, определяемой величиной сдвига, то есть нулевая нижняя граница модели черного была сдвинута.
Введение отрицательных процентных ставок также потребовало обновления метода интерполяции волатильности, котирующейся на рынке. Ниже показаны связи между волатильностью и моделями SABR:
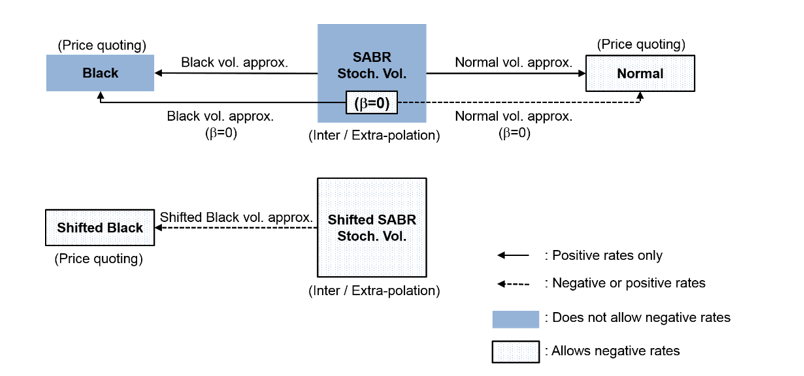
Как показано на рисунке, аппроксимации волатильности Черный (Black) и Нормальный (Normal) позволяют использовать модель SABR с формулами расчета цены опционов Черный (Black) и Нормальный (Normal). Тем не менее, хотя сама модель Normal допускает отрицательные ставки, а модель SABR имеет подразумеваемую аппроксимацию нормальной волатильности, базовая динамика модели SABR не допускает отрицательных ставок, если β = 0. Когда параметр β (Beta) SABR модель установлена в нуль, модель является моделью Normal SABR, которая позволяет вычислить подразумеваемые нормальные волатильности для отрицательных ставок.
В модели Shaded SABR аппроксимация волатильности Shilded Black может использоваться, чтобы позволить отрицательные ставки с фиксированной отрицательной нижней границей, определяемой величиной сдвига. Это достигается путем установки 'Shift' аргумент «имя-значение» SABR модели до положительного значения.
Можно вычислить подразумеваемые летучести с точки зрения параметров модели SABR либо для β = 0 (нормальный SABR), либо для любого другого значения β, допустимого моделью SABR (0 ≤ β ≤ 1), используя volatilities для функции SABR аналитический прайсер.
Следующие три типа подразумеваемых волатильности поддерживаются SABR аналитический прайсер и тип подразумеваемой волатильности, вычисленный volatilities функция зависит от параметров SABR при использовании SABR аналитический прайсер:
Подразумеваемые черные волатильности - SABR модель 'VolatilityType' аргумент name-value имеет значение "Black" и 'Shift' аргумент name-value имеет нулевое значение. Отрицательные ставки не допускаются.
Подразумеваемые просеянные черные волатильности - SABR модель 'VolatilityType' аргумент name-value имеет значение "Black" и 'Shift' аргумент name-value имеет положительное значение. Отрицательные ставки допускаются с нижней границей, определяемой величиной сдвига.
Подразумеваемые нормальные (холостяцкие) волатильности - The SABR модель 'VolatilityType' аргумент name-value имеет значение "Black" и 'Shift' аргумент name-value имеет нулевое значение. Отрицательные ставки разрешены, когда Beta входной аргумент равен нулю.