В этом разделе описываются характеристики решателя Global Optimization Toolbox. Раздел содержит рекомендации по более эффективному получению результатов.
Чтобы достичь лучших или более быстрых решений, сначала попробуйте настроить рекомендуемые решатели, установив соответствующие параметры или границы. Если результаты неудовлетворительны, попробуйте другие решатели.
| Требуемое решение | Сглаживание цели и ограничений | Непревзойденная цель или ограничения |
|---|---|---|
| Пояснение к «Желаемому решению» | Выбор между решателями для сглаживания проблем | Выбор между решателями для неконтактных проблем |
| Единое локальное решение | Функции Toolbox™ оптимизации; см. Таблицу решений по оптимизации | fminbnd, patternsearch, fminsearch, ga, particleswarm, simulannealbnd, surrogateopt |
| Несколько локальных решений | GlobalSearch, MultiStart | patternsearch, ga, particleswarm, simulannealbnd, или surrogateopt запущено из нескольких начальных точек x0 или из нескольких начальных популяций |
| Единое глобальное решение | GlobalSearch, MultiStart, patternsearch, particleswarm, ga, simulannealbnd, surrogateopt | patternsearch, ga, particleswarm, simulannealbnd, surrogateopt |
| Единое локальное решение с параллельной обработкой | MultiStart, функции панели инструментов оптимизации | patternsearch, ga, particleswarm, surrogateopt |
| Несколько локальных решений с параллельной обработкой | MultiStart | patternsearch, ga, или particleswarm запущено из нескольких начальных точек x0 или из нескольких начальных популяций |
| Единое глобальное решение с параллельной обработкой | MultiStart | patternsearch, ga, particleswarm, surrogateopt |
Чтобы понять значение терминов в «Желательном решении», рассмотрим пример
f (x) = 100x2 (1-x) 2-x,
который имеет локальные минимумы x1 вблизи 0 и x2 около 1:
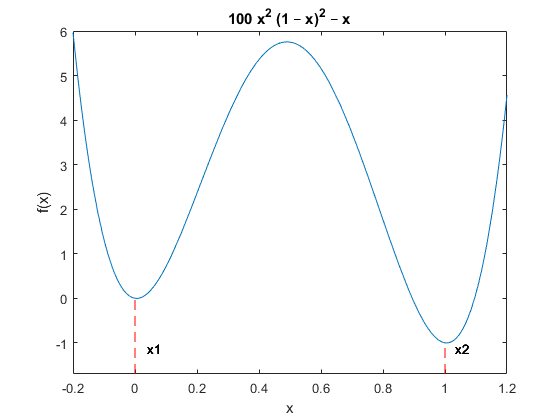
Минимумы расположены по адресу:
fun = @(x)(100*x^2*(x - 1)^2 - x);
x1 = fminbnd(fun,-0.1,0.1)
x1 =
0.0051
x2 = fminbnd(fun,0.9,1.1)
x2 =
1.0049Описание условий
| Термин | Значение |
|---|---|
| Единое локальное решение | Найдите одно локальное решение, точку x, где целевая функция f (x) является локальным минимумом. Дополнительные сведения см. в разделе Local vs. Global Optima. В примере обаx1 и x2 являются локальными решениями. |
| Несколько локальных решений | Найдите набор локальных решений. В примере полный набор локальных решений {x1,x2}. |
| Единое глобальное решение | Найдите точку x, где целевая функция f (x) является глобальным минимумом. В примере глобальное решение x2. |
Попробуй GlobalSearch во-первых. Он в наибольшей степени ориентирован на поиск глобального решения и имеет эффективный локальный решатель, fmincon.
Попробуй MultiStart далее. Он имеет эффективные локальные решатели и может выполнять поиск в различных начальных точках.
Попробуй patternsearch далее. Он менее эффективен, так как не использует градиенты. Однако patternsearch является надежным и более эффективным, чем остальные локальные решатели Чтобы найти глобальное решение, запустите patternsearch из различных начальных точек.
Попробуй surrogateopt далее. surrogateopt пытается найти глобальное решение, используя наименьшее количество объективных оценок функций. surrogateopt имеет больше накладных расходов на оценку функции, чем большинство других решателей. surrogateopt требует конечных границ и принимает целочисленные ограничения, линейные ограничения и нелинейные ограничения неравенства.
Попробуй particleswarm далее, если проблема не ограничена или имеет только связанные ограничения. Обычно, particleswarm является более эффективным, чем остальные решатели, и может быть более эффективным, чем patternsearch.
Попробуй ga далее. Он может обрабатывать все типы ограничений и обычно более эффективен, чем simulannealbnd.
Попробуй simulannealbnd последний. Он может обрабатывать проблемы без ограничений или связанных ограничений. simulannealbnd обычно является наименее эффективным решателем. Однако при достаточно медленном графике охлаждения можно найти глобальное решение.
GlobalSearch и MultiStart оба предоставляют несколько локальных решений. Синтаксис для получения нескольких решений см. в разделе Несколько решений. GlobalSearch и MultiStart отличаются следующими характеристиками:
MultiStart может найти больше локальных минимумов. Это потому, что GlobalSearch отклоняет много произведенных стартовых точек (начальные пункты для местного решения). По существу, GlobalSearch принимает начальную точку только тогда, когда определяет, что точка имеет хорошие шансы получить глобальный минимум. Напротив, MultiStart передает все сгенерированные начальные точки локальному решателю. Дополнительные сведения см. в разделе Алгоритм, используемый при поиске.
MultiStart предлагает выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin. GlobalSearch решатель использует только fmincon в качестве локального решателя.
GlobalSearch использует алгоритм поиска рассеяния для генерации начальных точек. Напротив, MultiStart генерирует точки равномерно случайным образом в пределах границ или позволяет предоставить собственные точки.
MultiStart может выполняться параллельно. См. раздел Использование параллельной обработки в инструментарии глобальной оптимизации.
Выберите подходящий решатель с наименьшим номером. Для проблем с целочисленными ограничениями используйте ga.
Использовать fminbnd сначала только на одномерных ограниченных задачах. fminbnd возможно быстро сходится в одном измерении.
Использовать patternsearch по любому другому типу проблем. patternsearch надежно сходится и обрабатывает все типы зависимостей.
Попробуй surrogateopt для задач, имеющих трудоемкие объективные функции. surrogateopt ищет глобальное решение. surrogateopt требует конечных границ и принимает целочисленные ограничения, линейные ограничения и нелинейные ограничения неравенства.
Попробуй fminsearch далее для низкоразмерных неограниченных задач. fminsearch не является таким общим, как patternsearch и может не сойтись. Для низкоразмерных задач, fminsearch проста в использовании, так как имеет мало вариантов настройки.
Попробуй particleswarm далее по неограниченным или ограниченным ограничениями проблемам. particleswarm имеет мало поддерживающей теории, но часто является эффективным алгоритмом.
Попробуй ga далее. ga имеет мало поддерживающей теории и часто менее эффективен, чем patternsearch или particleswarm. ga обрабатывает все типы ограничений. ga и surrogateopt являются единственными решателями панели инструментов глобальной оптимизации, принимающими целочисленные ограничения.
Попробуй simulannealbnd последнее для неограниченных проблем или для проблем с границами. simulannealbnd возможно сходится только для логарифмического графика охлаждения, который является чрезвычайно медленным. simulannealbnd принимает только связанные ограничения и часто менее эффективен, чем ga.
| Решающее устройство | Сходимость | Особенности |
|---|---|---|
GlobalSearch | Быстрая конвергенция в локальную оптимальную для решения проблем | Детерминированные итераты |
| Градиентный | ||
| Точки автоматического стохастического запуска | ||
| Эвристическое удаление многих начальных точек | ||
MultiStart | Быстрая конвергенция в локальную оптимальную для решения проблем | Детерминированные итераты |
| Может работать параллельно; см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации | ||
| Градиентный | ||
| Стохастические или детерминированные начальные точки, или комбинация обоих | ||
| Точки автоматического стохастического запуска | ||
| Выполняет все начальные точки | ||
Выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin | ||
patternsearch | Доказанная сходимость к локальному оптимуму; медленнее, чем решатели на основе градиента | Детерминированные итераты |
| Может работать параллельно; см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации | ||
| Без градиентов | ||
| Начальная точка, предоставленная пользователем | ||
surrogateopt | Доказанная конвергенция в глобальный оптимум для ограниченных проблем; медленнее, чем решатели на основе градиента; обычно останавливается, достигая предела оценки функции или другого предела | Стохастические итераты |
| Может работать параллельно; см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации | ||
| Наилучшим образом используется для выполнения трудоемких целевых функций | ||
| Требует связанных ограничений, принимает линейные ограничения и нелинейные ограничения неравенства | ||
| Допускает целочисленные ограничения; См. Оптимизация суррогата со смешанным целым числом | ||
| Без градиентов | ||
| Автоматические начальные точки или точки, предоставленные пользователем, или их комбинация | ||
particleswarm | Отсутствие доказательства сходимости | Стохастические итераты |
| Может работать параллельно; см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации | ||
| Популяционный | ||
| Без градиентов | ||
| Автоматическое начальное заполнение или заполнение, предоставляемое пользователем, или их сочетание | ||
| Только ограничивающие ограничения | ||
ga | Отсутствие доказательства сходимости | Стохастические итераты |
| Может работать параллельно; см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации | ||
| Популяционный | ||
| Без градиентов | ||
| Допускает целочисленные ограничения; см. Оптимизация смешанного целого ga | ||
| Автоматическое начальное заполнение или заполнение, предоставляемое пользователем, или их сочетание | ||
simulannealbnd | Доказано сходство с глобальным оптимумом для ограниченных проблем с очень медленным графиком охлаждения | Стохастические итераты |
| Без градиентов | ||
| Начальная точка, предоставленная пользователем | ||
| Только ограничивающие ограничения |
Объяснение некоторых характеристик:
Сходимость (Convergence) - решатели могут не сходиться ни к одному решению при запуске далеко от локального минимума. При запуске вблизи локального минимума решатели на основе градиента быстро сходятся к локальному минимуму для сглаживания проблем. patternsearch возможно сходится для широкого спектра задач, но сходимость медленнее, чем решатели на основе градиента. Оба ga и simulannealbnd может не сойтись в разумном количестве времени для некоторых проблем, хотя они часто эффективны.
Итераты - решатели выполняют итерацию для поиска решений. Шаги в итерации являются итерациями. Некоторые решатели имеют детерминированные итераты. Другие используют случайные числа и имеют стохастические итераты.
Градиенты (Gradients) - некоторые решатели при вычислении итератов используют оценочные или пользовательские производные. Другие решатели не используют и не оценивают производные, а используют только значения функций цели и ограничения.
Начальные точки (Start points) - большинство решателей требуют предоставить начальную точку для оптимизации, чтобы получить размерность переменных решения. ga и surrogateopt не требуют каких-либо начальных точек, поскольку они принимают размерность переменных принятия решения в качестве входных или выводят размерности из границ. Эти решатели автоматически генерируют начальную точку или заполнение или принимают точку или точки, которые вы предоставляете.
Сравните характеристики решателей Global Optimization Toolbox с решателями Optimization Toolbox.
| Решающее устройство | Сходимость | Особенности |
|---|---|---|
fmincon, fminunc, fseminf, lsqcurvefit, lsqnonlin | Проверенная квадратичная сходимость к локальной оптимизации для гладких проблем | Детерминированные итераты |
| Градиентный | ||
| Исходная точка, предоставленная пользователем | ||
fminsearch | Доказательств сходимости нет - контрпримеров не существует. | Детерминированные итераты |
| Без градиентов | ||
| Начальная точка, предоставленная пользователем | ||
| Без ограничений | ||
fminbnd | Проверенная сходимость к локальной оптимизации для гладких проблем, медленнее квадратичной. | Детерминированные итераты |
| Без градиентов | ||
| Заданный пользователем начальный интервал | ||
| Только одномерные задачи |
Все эти решатели панели инструментов оптимизации:
Иметь детерминированные итераты
Требуется начальная точка или интервал
Поиск только одного бассейна притяжения
GlobalSearch и MultiStart являются объектами. Что это значит для тебя?
Вы создаете GlobalSearch или MultiStart объект перед запуском проблемы.
Объект можно повторно использовать для выполнения нескольких задач.
GlobalSearch и MultiStart объекты являются контейнерами для алгоритмов и глобальных опций. Эти объекты используются для многократного запуска локального решателя. Локальный решатель имеет собственные опции.
Дополнительные сведения см. в документации по классам.