Граф - это совокупность узлов и рёбер, представляющих взаимосвязи:
Узлы - это вершины, соответствующие объектам.
Ребра - это соединения между объектами.
Рёбра графа иногда имеют Весы (Weights), которые указывают на прочность (или какой-либо другой атрибут) каждого соединения между узлами.
Эти определения являются общими, так как точное значение узлов и рёбер в графе зависит от конкретного приложения. Например, вы можете смоделировать дружеские отношения в социальной сети с помощью графика. Узлы графа - это люди, а рёбра представляют дружеские отношения. Естественное соответствие графов физическим объектам и ситуациям означает, что можно использовать графы для моделирования самых разнообразных систем. Например:
Связывание веб-страниц - узлы графика являются веб-страницами, а края представляют гиперссылки между страницами.
Аэропорты - узлы графика являются аэропортами, а рёбра представляют рейсы между аэропортами.
В MATLAB ®, graph и digraph функции создают объекты, представляющие неориентированные и направленные графики.
Неориентированные графики имеют рёбра, не имеющие направления. Кромки указывают двустороннюю взаимосвязь, так что каждая кромка может быть пройдена в обоих направлениях. На этом рисунке показан простой неориентированный граф с тремя узлами и тремя рёбрами.
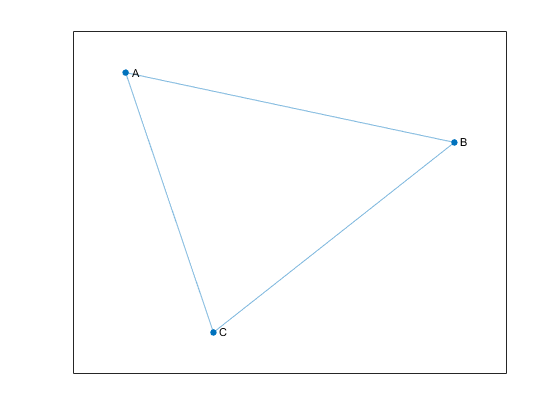
Направленные графы имеют рёбра с направлением. Кромки указывают на одностороннюю взаимосвязь, поскольку каждая кромка может быть пройдена только в одном направлении. На этом рисунке показан простой направленный граф с тремя узлами и двумя рёбрами.
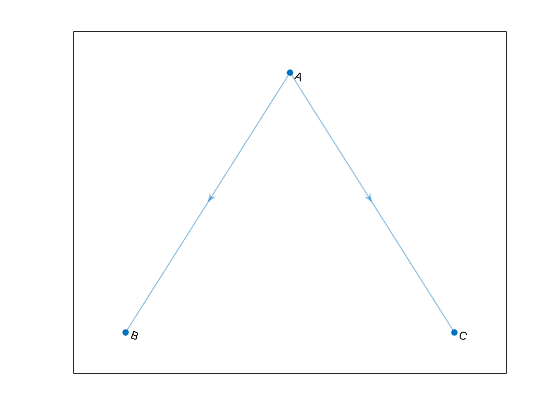
Точное положение, длина или ориентация рёбер на графике обычно не имеют значения. Другими словами, один и тот же граф может быть визуализирован несколькими различными способами путем перегруппировки узлов и/или искажения рёбер, пока базовая структура не изменяется.
Графики, созданные с помощью graph и digraph может иметь один или несколько самокольцов, которые являются ребрами, соединяющими узел с самим собой. Кроме того, графы могут иметь несколько рёбер с одними и теми же исходными и целевыми узлами, и тогда граф известен как мультиграф. Мультиграф может содержать или не содержать самокольцы.
Для целей функций алгоритма графов в MATLAB граф, содержащий узел с одним самокольцом, не является мультиграфом. Однако если граф содержит узел с несколькими самокольцами, он является мультиграфом.
Например, на следующем рисунке показан неориентированный мультиграф с самокольцами. Узел A имеет три самокольца, в то время как узел C имеет один. Граф содержит эти три условия, любое из которых делает его мультиграфом.
Узел A имеет три самокольца.
Узлы A и B имеют пять ребер между собой.
Узлы A и C имеют две кромки между ними.
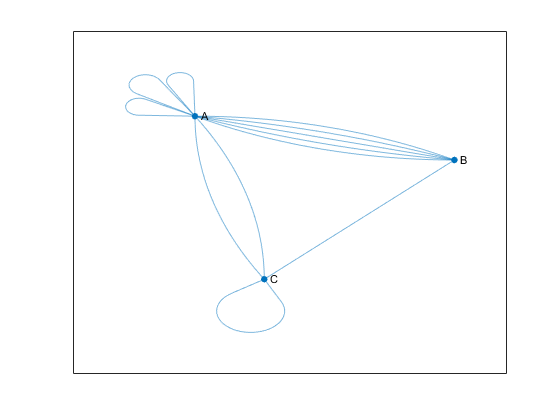
Чтобы определить, является ли данный граф мультиграфом, используйте ismultigraph функция.
Основные способы создания графика включают использование матрицы смежности или списка ребер.
Одним из способов представления информации в графе является квадратная матрица смежности. Ненулевые элементы в матрице смежности указывают край между двумя узлами, а значение элемента указывает вес края. Диагональные элементы матрицы смежности обычно равны нулю, но ненулевой диагональный элемент указывает самокольцевание или узел, который соединен с собой ребром.
При использовании graph для создания неориентированного графа матрица смежности должна быть симметричной. На практике матрицы часто являются треугольными, чтобы избежать повторения. Чтобы построить неориентированный граф, используя только верхний или нижний треугольник матрицы смежности, используйте graph(A,'upper') или graph(A,'lower') .
При использовании digraph для создания направленного графа матрица смежности не должна быть симметричной.
Для больших графов матрица смежности содержит много нулей и обычно является разреженной матрицей.
Невозможно создать мультиграф из матрицы смежности.
Например, рассмотрим этот неориентированный график.
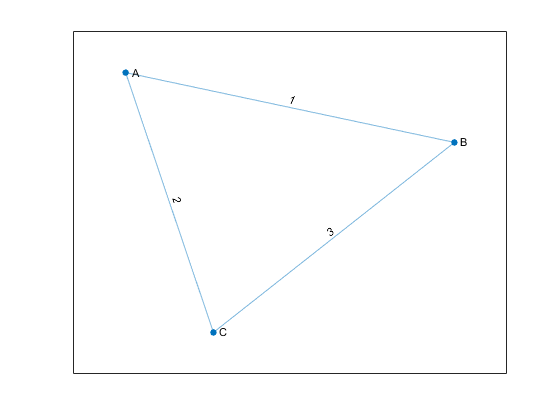
График можно представить с помощью этой матрицы смежности:
Чтобы построить график в MATLAB, введите:
A = [0 1 2; 1 0 3; 2 3 0];
node_names = {'A','B','C'};
G = graph(A,node_names)G =
graph with properties:
Edges: [3×2 table]
Nodes: [3×1 table]Вы можете использовать graph или digraph для создания графика с помощью матрицы смежности, или можно использовать adjacency для поиска взвешенной или невзвешенной разреженной матрицы смежности ранее существовавшего графа.
Другим способом представления информации на графике является перечисление всех рёбер.
Например, рассмотрим тот же неориентированный граф.

Теперь представляем график по списку ребер
C) 3
Из списка рёбер легко сделать вывод, что граф имеет три уникальных узла, A, B, и C, которые соединены тремя перечисленными ребрами. Если граф имеет отсоединенные узлы, они не будут найдены в списке рёбер и должны быть указаны отдельно.
В MATLAB список ребер разделен столбцами на исходные и целевые узлы. Для направленных графов направление рёбер (от источника к цели) важно, но для неориентированных графов источник и целевой узел взаимозаменяемы. Один из способов построения этого графика с использованием списка ребер состоит в использовании отдельных входных данных для исходных узлов, целевых узлов и весов ребер:
source_nodes = {'A','A','B'};
target_nodes = {'B','C','C'};
edge_weights = [1 2 3];
G = graph(source_nodes, target_nodes, edge_weights);Оба graph и digraph обеспечение возможности построения простого графа или мультиграфа из списка рёбер. После построения графа G, вы можете посмотреть на края (и их свойства) с помощью команды G.Edges. Порядок ребер в G.Edges сортируется по исходному узлу (первый столбец) и вторично по целевому узлу (второй столбец). Для неориентированных графиков узел с меньшим индексом перечисляется как исходный узел, а узел с большим индексом - как целевой узел.
С момента основополагающего осуществления graph и digraph зависит от разреженных матриц, применяется много одинаковых затрат на индексирование. Использование одного из предыдущих методов для построения графика из трех пар (source,target,weight) быстрее, чем создать пустой граф и итеративно добавить больше узлов и рёбер. Для достижения максимальной производительности сократите число вызовов graph, digraph, addedge, addnode, rmedge, и rmnode.
По умолчанию все узлы на графике создаются с помощью graph или digraph пронумерованы. Поэтому всегда можно ссылаться на них по их числовому индексу узла.
Если граф имеет имена узлов (то есть G.Nodes содержит переменную Name), то также можно ссылаться на узлы графа, используя их имена. Таким образом, именованные узлы в графе могут быть обозначены либо их индексами узлов, либо именами узлов. Например, узел 1 может вызываться, 'A'.
Термин ИД узла охватывает оба аспекта идентификации узла. Идентификатор узла ссылается как на индекс узла, так и на имя узла.
Для удобства MATLAB запоминает, какой тип идентификатора узла используется при вызове большинства функций графика. Таким образом, если ссылаться на узлы в графе по их индексам узлов, большинство функций графов возвращает числовой ответ, который также относится к узлам по их индексам.
A = [0 1 1 0; 1 0 1 0; 1 1 0 1; 0 0 1 0];
G = graph(A,{'a','b','c','d'});
p = shortestpath(G,1,4)
p =
1 3 4
Однако если ссылаться на узлы по их именам, то большинство функций графа возвращает ответ, который также относится к узлам по их именам (содержится в массиве ячеек из символьных векторов или строкового массива).
p1 = shortestpath(G,'a','d')
p1 =
1×3 cell array
{'a'} {'c'} {'d'}Использовать findnode для поиска числового идентификатора узла для данного имени узла. И наоборот, для данного числового идентификатора узла индексировать в G.Nodes.Name для определения соответствующего имени узла.
После построения graph или digraph можно использовать различные функции для изменения структуры графика или для определения количества узлов или рёбер графа. В этой таблице перечислены некоторые доступные функции для изменения или запроса graph и digraph объекты.
addedge | Добавление одного или нескольких ребер к графу |
rmedge | Удаление одного или нескольких ребер из графика |
addnode | Добавление одного или нескольких узлов в график |
rmnode | Удаление одного или нескольких узлов из графика |
findnode | Поиск определенного узла на графике |
findedge | Поиск определенного ребра на графике |
numnodes | Найти количество узлов в графике |
numedges | Найти число рёбер в графике |
edgecount | Количество ребер между указанными узлами |
flipedge | Изменение направления направленных рёбер графика на противоположное |
reordernodes | Перестановка порядка узлов в графе |
subgraph | Извлечь подграф |
Некоторые общие примеры изменения графика см. в разделе Изменение узлов и рёбер существующего графика.