Одним из наиболее важных и распространенных применений числовой линейной алгебры является решение линейных систем, которые могут быть выражены в виде A*x = b. Когда A является большой разреженной матрицей, можно решить линейную систему с помощью итеративных методов, которые позволяют найти компромисс между временем выполнения вычисления и точностью решения. В этом разделе описываются итерационные методы, доступные в MATLAB ® для решения уравненияA*x = b.
Существует два типа методов решения линейных уравнений A*x = b:
Прямые методы - варианты гауссовой элиминации. Эти методы используют отдельные матричные элементы непосредственно посредством матричных операций, таких как LU, QR или факторизация Холеского. Можно использовать прямые методы для решения линейных уравнений с высоким уровнем точности, но эти методы могут быть медленными при работе на больших разреженных матрицах. Скорость решения линейной системы прямым методом сильно зависит от плотности и рисунка заполнения матрицы коэффициентов.
Например, этот код решает небольшую линейную систему.
A = magic(5); b = sum(A,2); x = A\b; norm(A*x-b)
ans = 1.4211e-14
MATLAB реализует прямые методы через операторы матричного деления / и \, а также такие функции, как decomposition, lsqminnorm, и linsolve.
Итеративные методы дают аппроксимированное решение линейной системы после конечного числа шагов. Эти методы полезны для больших систем уравнений, в которых целесообразно отрегулировать точность для более короткого времени выполнения. Итерационные методы используют матрицу коэффициентов только косвенно, через произведение матрица-вектор или абстрактный линейный оператор. Итеративные методы могут использоваться с любой матрицей, но они обычно применяются к большим разреженным матрицам, для которых прямые решения являются медленными. Скорость решения линейной системы косвенным методом не так сильно зависит от шаблона заполнения матрицы коэффициентов, как прямой метод. Однако использование итеративного способа обычно требует настройки параметров для каждой конкретной проблемы.
Например, этот код решает большую разреженную линейную систему, которая имеет симметричную матрицу положительных определенных коэффициентов.
A = delsq(numgrid('L',400));
b = ones(size(A,1),1);
x = pcg(A,b,[],1000);
norm(b-A*x)pcg converged at iteration 796 to a solution with relative residual 9.9e-07. ans = 3.4285e-04
MATLAB реализует множество итеративных методов, которые имеют различные сильные и слабые стороны в зависимости от свойств матрицы коэффициентов A.
Прямые методы обычно являются более быстрыми и более широко применимыми, чем косвенные методы, если для их выполнения имеется достаточно ресурсов хранения. Как правило, необходимо попытаться использовать x = A\b во-первых. Если прямое решение слишком медленное, то можно попробовать использовать итеративные методы.
Большинство итеративных алгоритмов, решающих линейные уравнения, следуют аналогичному процессу:
Начните с начального предположения для вектора решения x0. (Обычно это вектор нулей, если не указано лучшее предположение.)
Вычислить остаточную норму res = norm(b-A*x0).
Сравните остаток с указанным допуском. Если res <= tol, завершить вычисление и вернуть вычисленный ответ для x0.
Обратиться A*x0 и обновить величину и направление вектора x0 на основе величины остатка и других рассчитанных количеств. Это шаг, на котором выполняется большинство вычислений.
Повторяйте шаги 2-4 до значения x0 достаточно хорошо, чтобы удовлетворить допуск.
Итеративные методы отличаются тем, как они обновляют величину и направление x0 на этапе 4, и некоторые имеют несколько другие критерии сходимости на этапах 2 и 3, но это фиксирует основной процесс, которому следуют все итеративные решатели.
MATLAB имеет несколько функций, реализующих итеративные методы для систем линейных уравнений. Эти методы предназначены для решения Ax = b или минимизации нормы | | b - Ax | |. Некоторые из этих методов имеют сходство и основаны на одних и тех же алгоритмах, но каждый алгоритм имеет преимущества в определенных ситуациях [1], [2].
Описание | Примечания |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
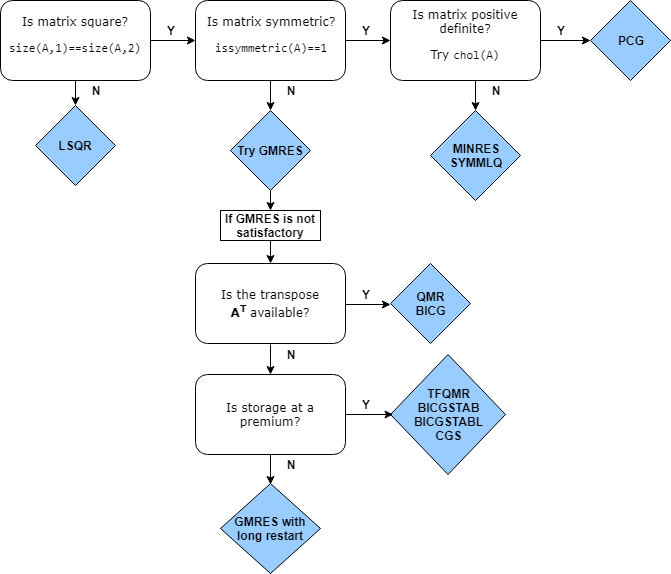
Эта блок-схема итеративных решателей в MATLAB дает приблизительное представление о ситуациях, в которых полезен каждый решатель. Как правило, можно использовать gmres практически для всех квадратных, несимметричных задач. Есть некоторые случаи, когда алгоритмы градиентов биконъюгата (bicg, bicgstab, cgs, и так далее) эффективнее, чем gmres, но их непредсказуемое поведение сходимости часто делает gmres лучший первоначальный выбор.
Скорость сходимости итеративных методов зависит от спектра (собственных значений) матрицы коэффициентов. Поэтому можно улучшить сходимость и стабильность большинства итеративных методов, преобразовав линейную систему, чтобы она имела более благоприятный спектр (кластеризованные собственные значения или число условий около 1). Это преобразование выполняется путем применения к системе второй матрицы, называемой устройством предварительного кондиционирования. Этот процесс преобразует линейную систему
b
в эквивалентную систему
Идеальный блок предварительного кондиционирования преобразует матрицу коэффициентов А в единичную матрицу, поскольку любой итеративный метод будет сходиться в одной итерации с таким блоком предварительного кондиционирования. На практике поиск хорошего предварительного условия требует компромиссов. Преобразование выполняется одним из трех способов: левое предварительное кондиционирование, правое предварительное кондиционирование или разделенное предварительное кондиционирование.
Первый случай называется левым предварительным кондиционированием, поскольку матрица М предварительного кондиционирования появляется слева от А:
1 b).
Эти итеративные решатели используют левое предварительное кондиционирование:
При правильном предварительном кондиционировании справа от А появляется М:
= b.
Эти итеративные решатели используют правильное предварительное кондиционирование:
Наконец, для матриц симметричных коэффициентов A, разделение предварительного кондиционирования гарантирует, что преобразованная система все еще симметрична. Предварительное кондиционирующее устройство HHT разделяется, и на разных сторонах А появляются коэффициенты:
(H − 1b)
Алгоритм решателя для разделенных систем предварительного кондиционирования основан на вышеприведенном уравнении, но на практике нет необходимости вычислять Н. Алгоритм решателя умножается и решает с помощью M непосредственно.
Эти итеративные решатели используют разделенное предварительное кондиционирование:
Во всех случаях для ускорения сходимости итеративного метода выбирают устройство М предварительного кондиционирования. Когда остаточная ошибка итеративного решения стагнирует или делает незначительный прогресс между итерациями, это часто означает, что необходимо создать матрицу предварительного условия для включения в задачу.
Итеративные решатели в MATLAB позволяют задать одну матрицу предварительного условия M или два коэффициента матрицы предварительного условия, так что M = M1M2. Это упрощает определение предварительного условия в его факторизованной форме, например M = LU. Следует отметить, что в случае разделения, где M = HHT также имеет место, связь между M1 и M2 входные данные и коэффициенты Н.
В некоторых случаях предварительные условия возникают естественным образом в математической модели данной задачи. При отсутствии естественных предварительных условий можно использовать одну из неполных факторизаций в этой таблице для создания матрицы предварительных условий. Неполные факторизации являются по существу неполными прямыми решениями, которые быстро вычисляются.
| Функция | Факторизация | Описание |
|---|---|---|
ilu |
| Неполная факторизация LU для квадратных или прямоугольных матриц. |
ichol |
* | Неполная факторизация Холеского для симметричных положительных определённых матриц. |
Дополнительные сведения см. в разделе Неполные факторизации ilu и ichol.
Рассмотрим пятиточечное конечное дифференциальное приближение к уравнению Лапласа в квадратной двумерной области. Следующие команды используют метод предварительно кондиционированного сопряженного градиента (PCG) с устройством предварительного кондиционирования M = L*L', где L - неполный коэффициент Холеского с нулевым заполнением A. Для этой системы, pcg не может найти решение без указания матрицы предварительного условия.
A = delsq(numgrid('S',250));
b = ones(size(A,1),1);
tol = 1e-3;
maxit = 100;
L = ichol(A);
x = pcg(A,b,tol,maxit,L,L');pcg converged at iteration 92 to a solution with relative residual 0.00076.
pcg для достижения заданного допуска требуется 92 итерации. Однако использование другого устройства предварительного кондиционирования может дать лучшие результаты. Например, использование ichol построить модифицированный неполный Cholesky позволяет pcg для соответствия указанному допуску только после 39 итераций.
L = ichol(A,struct('type','nofill','michol','on')); x = pcg(A,b,tol,maxit,L,L');
pcg converged at iteration 39 to a solution with relative residual 0.00098.
Для решения сложных вычислительных задач может потребоваться более высокий уровень предварительного кондиционирования, чем тот, который был создан ilu или ichol непосредственно. Например, может потребоваться создать средство предварительного кондиционирования лучшего качества или минимизировать объем выполняемых вычислений. В этих случаях можно использовать равновесие, чтобы сделать матрицу коэффициентов более диагонально доминирующей (что может привести к лучшему качеству предварительного кондиционирования) и переупорядочение, чтобы минимизировать количество ненулевых в матричных факторах (что может снизить требования к памяти и может улучшить эффективность последующих вычислений).
При использовании уравновешивания и переупорядочивания для создания средства предварительного кондиционирования выполняется следующее:
Использовать equilibrate на матрице коэффициентов.
Переупорядочить уравновешенную матрицу с помощью разреженной функции переупорядочивания матрицы, такой как dissect или symrcm.
Создание окончательного предварительного условия с помощью ilu или ichol.
Вот пример, который использует равновесие и переупорядочение, чтобы создать устройство предварительного кондиционирования для матрицы разреженных коэффициентов.
Создание матрицы коэффициентов A и вектор единиц b для правой стороны линейного уравнения. Расчет оценки номера условия для A.
load west0479;
A = west0479;
b = ones(size(A,1),1);
condest(A)ans = 1.4244e+12
Использовать equilibrate для улучшения номера условия матрицы коэффициентов.
[P,R,C] = equilibrate(A); Anew = R*P*A*C; bnew = R*P*b; condest(Anew)
ans = 5.1042e+04
Переупорядочить уравновешенную матрицу с помощью dissect.
q = dissect(Anew); Anew = Anew(q,q); bnew = bnew(q);
Создание предварительного условия с использованием неполной факторизации логической единицы.
[L,U] = ilu(Anew);
Решите линейную систему с помощью gmres использование матриц предварительного условия, допуск 1e-10, 50 максимальных внешних итераций и 30 внутренних итераций.
tol = 1e-10; maxit = 50; restart = 30; [xnew, flag, relres] = gmres(Anew,bnew,restart,tol,maxit,L,U); x(q) = xnew; x = C*x(:);
Теперь сравните relres относительный остаток, возвращенный gmres (включая предварительные условия) к относительному остатку без предварительных условий resnew и относительный остаток без равновесия res. Результаты показывают, что, хотя все линейные системы эквивалентны, различные методы применяют разные веса к каждому элементу, и это может значительно повлиять на значение остатка.
relres resnew = norm(Anew*xnew - bnew) / norm(bnew) res = norm(A*x - b) / norm(b)
relres = 8.7537e-11 resnew = 3.6805e-08 res = 5.1415e-04
Итеративные решатели в MATLAB не требуют предоставления числовой матрицы для A. Поскольку вычисления, выполняемые решателями, используют результат умножения матрица-вектор A*x или A'*xвместо этого можно предоставить функцию, которая вычисляет результат этих линейных операций. Функция, вычисляющая эти величины, часто называется линейным оператором.
Помимо использования линейного оператора вместо матрицы коэффициентов A, можно также использовать линейный оператор вместо матрицы для предварительного условия M. В этом случае функции необходимо вычислить M\x или M'\x, как указано на справочной странице решателя.
Использование линейных операторов позволяет использовать шаблоны в A или M чтобы вычислить значение линейных операций более эффективно, чем если бы решатель использовал матрицу явно для выполнения полного умножения матрица-вектор. Это также означает, что вам не нужна память для хранения коэффициентов или матриц предварительного кондиционирования, так как линейный оператор обычно вычисляет результат умножения матрица-вектор без формирования матрицы вообще.
Например, рассмотрим матрицу коэффициентов
A = [2 -1 0 0 0 0;
-1 2 -1 0 0 0;
0 -1 2 -1 0 0;
0 0 -1 2 -1 0;
0 0 0 -1 2 -1;
0 0 0 0 -1 2];Когда A умножает вектор, большинство элементов в полученном векторе равны нулю. Ненулевые элементы в результате соответствуют ненулевым тридиагональным элементам A. Итак, для данного вектора x, функция линейного оператора просто должна сложить три вектора для вычисления значения A*x:
function y = linearOperatorA(x) y = -1*[0; x(1:end-1)] ... + 2*x ... + -1*[x(2:end); 0]; end
Для большинства итеративных решателей требуется функция линейного оператора для A для возврата значения A*x. Аналогично, для матрицы предварительного кондиционирования M, функция, как правило, должна рассчитать M\x. Для решателей lsqr, qmr, и bicg, функции линейного оператора также должны возвращать значение для A'*x или M'\x по запросу. Примеры и описания функций линейных операторов см. на страницах ссылок итерационного решателя.
[1] Барретт, Р., М. Берри, Т. Ф. Чан и др., Шаблоны для решения линейных систем: строительные блоки для итеративных методов, SIAM, Филадельфия, 1994.
[2] Саад, Юсеф, Итерационные методы разреженных линейных уравнений. Издательская компания PWS, 1996.