Триангуляции часто используются для представления 2-D и 3-D геометрических областей в таких областях применения, как компьютерная графика, физическое моделирование, географические информационные системы, медицинская визуализация и многое другое. Отображаемый здесь многоугольник карты
может быть представлена триангуляцией на карте, показанной ниже.
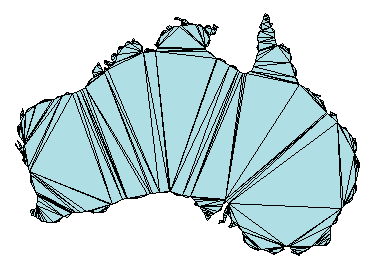
Триангуляция разлагает сложный многоугольник на совокупность более простых треугольных многоугольников. Эти многоугольники можно использовать для разработки алгоритмов на основе геометрии или графических приложений.
Аналогично, можно представить границу 3-D геометрической области с помощью триангуляции. На рисунке ниже показан выпуклый корпус набора точек в 3-D пространстве. Каждая грань корпуса представляет собой треугольник.
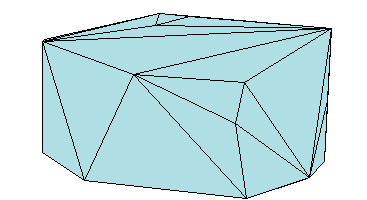
MATLAB ® использует матричный формат для представления триангуляций. Этот формат состоит из двух частей:
Вершины, представленные в виде матрицы, в которой каждая строка содержит координаты точки в триангуляции.
Связность триангуляции, представляемая в виде матрицы, в которой каждая строка определяет треугольник или тетраэдр.
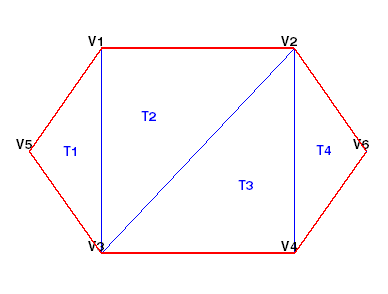
На этом рисунке показана простая триангуляция 2-D.
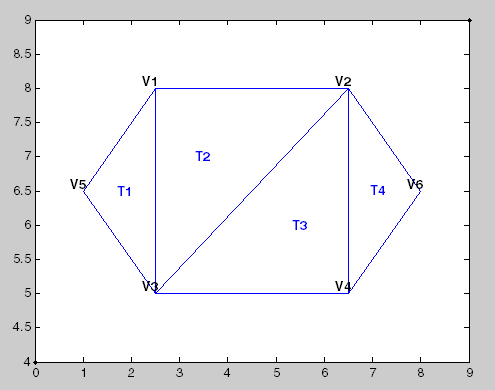
В следующей таблице приведены сведения о вершинах.
| Вершины | ||
|---|---|---|
| Идентификатор вершины | координата X | координата Y |
| V1 | 2.5 | 8.0 |
| V2 | 6.5 | 8.0 |
| V3 | 2.5 | 5.0 |
| V4 | 6.5 | 5.0 |
| V5 | 1.0 | 6.5 |
| V6 | 8.0 | 6.5 |
Данные в предыдущей таблице сохраняются как матрица в среде MATLAB. Идентификаторы вершин - это метки, используемые для идентификации определенных вершин. Они показаны для иллюстрации концепции идентификатора вершины, но не хранятся явно. Вместо этого номера строк матрицы служат идентификаторами вершин.
Данные о связности триангуляции показаны в этой таблице.
| Возможность соединения | |||
|---|---|---|---|
| Идентификатор треугольника | Идентификаторы ограничивающих вершин | ||
| T1 | 5 | 3 | 1 |
| T2 | 3 | 2 | 1 |
| T3 | 3 | 4 | 2 |
| T4 | 4 | 6 | 2 |
Данные в этой таблице хранятся как матрица в среде MATLAB. Идентификаторы треугольников - это метки, используемые для идентификации определенных треугольников. Они показаны для иллюстрации концепции идентификатора треугольника, но не хранятся явно. Вместо этого номера строк матрицы служат идентификаторами треугольника.
Вы можете увидеть этот треугольник T1 определяется тремя вершинами, {V5, V3, V1}. Аналогично, T4 определяется вершинами, {V4, V6, V2}. Этот формат естественным образом распространяется на более высокие измерения, которые требуют дополнительных столбцов данных. Например, тетраэдр в 3-D пространстве определяется четырьмя вершинами, каждая из которых имеет три координаты, (x, y, z).
С помощью MATLAB можно представлять и запрашивать следующие типы триангуляций:
2-D триангуляции, состоящие из треугольников, ограниченных вершинами и ребрами
3-D триангуляции поверхности, состоящие из треугольников, ограниченных вершинами и ребрами
3-D триангуляции, состоящие из тетраэдров, ограниченных вершинами, ребрами и гранями
Матричный формат обеспечивает компактное низкоуровневое представление на основе массива для триангуляций. При использовании триангуляций для разработки алгоритмов может потребоваться дополнительная информация о геометрических свойствах, топологии и смежности.
Например, перед выводом на печать аннотированной триангуляции, показанной ниже, можно вычислить углы наклона треугольника. В этом случае для отображения меток треугольника (T1, T2 и т.д.) в каждом треугольнике используются указатели. Если требуется нарисовать границу красным цветом, необходимо определить кромки, на которые ссылается только один треугольник.
Вы можете использовать triangulation для создания в памяти представления любых 2-D или 3-D данных триангуляции, которые находятся в матричном формате, например матричных выходных данных delaunay функции или других программных средств. Когда данные представлены с помощью triangulation, можно выполнять топологические и геометрические запросы, которые можно использовать для разработки геометрических алгоритмов. Например, можно найти треугольники или тетраэдры, присоединенные к вершине, те, которые имеют общее ребро, их циркумцентры и другие элементы.
Можно создать triangulation одним из двух способов:
Передача существующих данных в матричном формате в triangulation. Эти данные могут быть выходными данными функции MATLAB, например, delaunay или convhull. Можно также импортировать данные триангуляции, созданные другим программным приложением. При работе с импортированными данными убедитесь, что данные связности ссылаются на массив вершин с помощью индексирования на основе 1 вместо индексирования на основе 0.
Передача набора точек delaunayTriangulation. Полученная триангуляция Делоне является особым видом triangulation. Это означает, что вы можете выполнить любое triangulation запрос данных, а также любой запрос, специфичный для Delaunay. В более формальных терминах языка MATLAB delaunayTriangulation является подклассом triangulation.
Создание триангуляции из матричных данных
В этом примере показано, как использовать данные матрицы триангуляции, чтобы создать триангуляцию, исследовать ее и исследовать, что она может сделать.
Создание матрицы, P, который содержит данные вершины.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];Определите возможности подключения, T.
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];Создать triangulation из этих данных.
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Доступ к свойствам в triangulation таким же образом осуществляется доступ к полям struct. Например, проверьте Points свойство, содержащее координаты вершин.
TR.Points
ans = 6×2
2.5000 8.0000
6.5000 8.0000
2.5000 5.0000
6.5000 5.0000
1.0000 6.5000
8.0000 6.5000
Затем изучите возможности подключения.
TR.ConnectivityList
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Points и ConnectivityList свойства определяют матричные данные для триангуляции.
triangulation класс - это обертка вокруг матричных данных. Реальной выгодой является полезность triangulation методы классов. Методы подобны функциям, принимающим triangulation и другие соответствующие входные данные.
triangulation класс обеспечивает простой способ индексации в ConnectivityList матрица свойств. Доступ к первому треугольнику в триангуляции.
TR.ConnectivityList(1,:)
ans = 1×3
5 3 1
Другой способ получить первый треугольник TR(1,:).
Проверьте первую вершину первого треугольника.
TR(1,1)
ans = 5
Проверьте вторую вершину первого треугольника.
TR(1,2)
ans = 3
Теперь изучите все треугольники в триангуляции.
TR(:,:)
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Использовать triplot для построения графика triangulation. triplot функция не является triangulation метод, но он принимает и может построить график triangulation.
figure
triplot(TR)
axis equal
Используйте triangulation способ, freeBoundaryдля запроса свободной границы и выделения ее на графике. Этот метод возвращает кромки триангуляции, которые совместно используются только одним треугольником. Возвращенные ребра выражаются в терминах идентификаторов вершин.
boundaryedges = freeBoundary(TR)';
Теперь постройте график граничных кромок красной линией.
hold on plot(P(boundaryedges,1),P(boundaryedges,2),'-r','LineWidth',2) hold off

Вы можете использовать freeBoundary метод проверки триангуляции. Например, при наблюдении красных ребер во внутренней части триангуляции это указывает на проблему соединения треугольников.
Создание триангуляции Использование delaunayTriangulation
В этом примере показано, как создать триангуляцию Делоне с помощью delaunayTriangulation.
При создании триангуляции Делоне с помощью delaunayTriangulation , вы автоматически получаете доступ к triangulation методы, потому что delaunayTriangulation является подклассом triangulation.
Создать delaunayTriangulation из набора точек.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Constraints: []
Получающееся delaunayTriangulation объект имеет свойства, Points и ConnectivityList, прямо как triangulation объект.
Вы можете получить доступ к триангуляции с помощью прямого индексирования, как triangulation. Например, проверьте связность первого треугольника.
DT(1,:)
ans = 1×3
5 3 1
Затем изучите связность всей триангуляции.
DT(:,:)
ans = 4×3
5 3 1
3 4 1
1 4 2
4 6 2
Используйте triplot для построения графика триангуляции.
triplot(DT)
axis equal
Родительский класс, triangulation, обеспечивает incenter способ вычисления incenters каждого треугольника.
IC = incenter(DT)
IC = 4×2
1.8787 6.5000
3.5000 6.0000
5.5000 7.0000
7.1213 6.5000
Возвращенное значение, IC, является массивом координат, представляющих наклоны треугольников.
Теперь используйте incenters, чтобы найти позиции для размещения меток треугольника на графике.
hold on numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off

Вместо создания триангуляции Делоне delaunayTriangulation, вы можете использовать delaunay создать данные о связности триангуляции, а затем передать данные о связности в triangulation. Например,
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
T = delaunay(P);
TR = triangulation(T,P);
IC = incenter(TR);В этом примере допустимы оба подхода, но если требуется создать триангуляцию Делоне и выполнить с ней запросы, то следует использовать delaunayTriangulation по следующим причинам:
delaunayTriangulation класс предоставляет дополнительные методы, полезные для работы с триангуляциями. Например, можно выполнить поиск ближайшего соседа и точки в треугольнике.
Она позволяет редактировать триангуляцию для добавления, перемещения или удаления точек.
Он позволяет создавать зависимые триангуляции Делоне. Это позволяет создать триангуляцию для 2-D домена.
delaunay | delaunayTriangulation | freeBoundary | triangulation | triplot