Триангуляции Делоне широко используются в научных вычислениях во многих различных приложениях. Хотя существуют многочисленные алгоритмы вычисления триангуляций, именно благоприятные геометрические свойства триангуляции Делоне делают её столь полезной.
Фундаментальным свойством является критерий Делоне. В случае 2-D триангуляций это часто называют критерием пустой окружности. Для набора точек в 2-D триангуляция Делоне этих точек гарантирует, что окружность, связанная с каждым треугольником, не содержит другой точки во внутренней части. Это свойство имеет важное значение. На приведенном ниже рисунке окружность, связанная с T1 пуст. Он не содержит точки в своем интерьере. Окружность, связанная с T2 пуст. Он не содержит точки в своем интерьере. Эта триангуляция является триангуляцией Делоне.
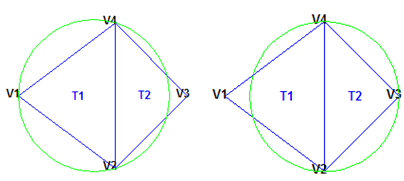
Треугольники ниже разные. Окружность, связанная с T1 не пуст. Он содержит V3 в его интерьере. Окружность, связанная с T2 не пуст. Он содержит V1 в его интерьере. Эта триангуляция не является триангуляцией Делоне.
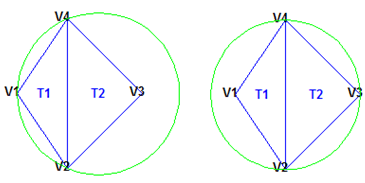
Говорят, что треугольники Делоне имеют «хорошую форму», потому что при выполнении свойства пустой окружности треугольники с большими внутренними углами выбираются над треугольниками с малыми внутренними углами. Треугольники в триангуляции не Делоне имеют острые углы в вершинах V2 и V4. Если край {V2, V4} были заменены на соединение кромок V1 и V3минимальный угол будет максимизирован, и триангуляция станет триангуляцией Делоне. Кроме того, триангуляция Делоне соединяет точки ближайшим соседом. Эти две характеристики, хорошо сформированные треугольники и отношение ближайшего соседа, имеют важные последствия на практике и мотивируют использование триангуляций Делоне в интерполяции разрозненных данных.
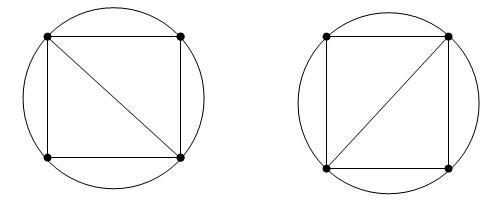
Хотя свойство Делоне хорошо определено, топология триангуляции не является уникальной при наличии вырожденных наборов точек. В двух измерениях вырожденности возникают, когда четыре или более уникальных точек лежат на одной окружности. Вершины квадрата, например, имеют неуникальную триангуляцию Делоне.
Свойства триангуляций Делоне распространяются на более высокие размеры. Триангуляция 3-D набора точек состоит из тетраэдров. На следующей иллюстрации показана простая 3-D триангуляция Делоне, состоящая из двух тетраэдров. Показано, что циркумсфера одного тетраэдра выделяет критерий пустой циркумсферы.
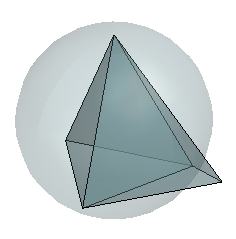
3D триангуляция Delaunay производит tetrahedra, которые удовлетворяют пустой критерий описанной сферы.
MATLAB ® предоставляет два способа создания триангуляций Delaunay :
Функции delaunay и delaunayn
delaunayTriangulation класс
delaunay функционируйте поддерживает создание 2-х и 3D триангуляций Delaunay. delaunayn функция поддерживает создание триангуляций Delaunay в 4-D и выше.
Совет
Создание триангуляций Делоне в измерениях выше 6-D обычно нецелесообразно для наборов точек от умеренных до больших из-за экспоненциального роста требуемой памяти.
delaunayTriangulation класс поддерживает создание триангуляций Delaunay в 2-D и 3-D. Он предоставляет множество методов, которые полезны для разработки алгоритмов на основе триангуляции. Эти методы класса подобны функциям, но они ограничены работой с триангуляциями, созданными с помощью delaunayTriangulation. delaunayTriangulation класс также поддерживает создание связанных конструкций, таких как выпуклый корпус и диаграмма Вороного. Он также поддерживает создание зависимых триангуляций Делоне.
Подводя итог:
delaunay функция полезна, когда требуются только основные данные триангуляции, и эти данные являются достаточно полными для приложения.
delaunayTriangulation класс предлагает больше функциональных возможностей для разработки приложений на основе триангуляции. Это полезно, когда требуется триангуляция и требуется выполнить любую из следующих операций:
Найдите в триангуляции треугольники или тетраэдры, содержащие точку запроса.
Триангуляция используется для поиска ближайшей соседней точки.
Запрос топологической смежности или геометрических свойств триангуляции.
Измените триангуляцию, чтобы вставить или удалить точки.
Ограничение ребер в триангуляции - это называется зависимой триангуляцией Делоне.
Выполните триангуляцию многоугольника и, при необходимости, удалите треугольники, находящиеся вне области.
Используйте триангуляцию Делоне для вычисления выпуклого корпуса или диаграммы Вороного.
delaunay и delaunayn функции берут набор точек и создают триангуляцию в матричном формате. Дополнительные сведения об этой структуре данных см. в разделе Формат матрицы триангуляции. В 2-D, delaunay функция часто используется для создания триангуляции, которая может использоваться для построения графика поверхности, определенной в терминах набора рассеянных точек данных. В этом приложении важно отметить, что этот подход может использоваться только в том случае, если поверхность является однозначной. Например, его нельзя использовать для построения сферической поверхности, поскольку существует две z значения, соответствующие единице (x, y) координата. Простой пример демонстрирует, как delaunay функция может использоваться для построения графика поверхности, представляющей набор данных выборки.
В этом примере показано, как использовать delaunay функция, чтобы создать 2-ю триангуляцию Delaunay из набора данных подводной горы. Подводная гора - подводная гора. Набор данных состоит из набора долготы (x) и широты (yместа и соответствующие отметки подводных гор (z), измеренный в этих координатах.
Загрузите набор данных подводной горы и просмотрите (x, y) данные как график рассеяния.
load seamount plot(x,y,'.','markersize',12) xlabel('Longitude'), ylabel('Latitude') grid on

Создание триангуляции Делоне из этого набора точек и использование triplot для построения графика триангуляции на существующем рисунке.
tri = delaunay(x,y); hold on, triplot(tri,x,y), hold off

Добавьте данные глубины (z) от подводной горы, чтобы поднять вершины и создать поверхность. Создание новой фигуры и использование trimesh для печати поверхности в каркасном режиме.
figure hidden on trimesh(tri,x,y,z) xlabel('Longitude'),ylabel('Latitude'),zlabel('Depth in Feet');

Для печати поверхности в затененном режиме используйте команду trisurf вместо trimesh.
3D триангуляция Delaunay также может быть создана, используя delaunay функция. Эта триангуляция состоит из тетраэдров.
Этот пример показывает, как создать 3D триангуляцию Delaunay случайного набора данных. Триангуляция выводится на печать с использованием tetramesh, и FaceAlpha добавляет прозрачность в график.
rng('default') X = rand([30 3]); tet = delaunay(X); faceColor = [0.6875 0.8750 0.8984]; tetramesh(tet,X,'FaceColor', faceColor,'FaceAlpha',0.3);

MATLAB обеспечивает delaunayn для поддержки создания триангуляций Делоне в размерности 4-D и выше. Две взаимодополняющие функции tsearchn и dsearchn также предусмотрены для поддержки пространственного поиска N-D триангуляций. Дополнительные сведения о поиске на основе триангуляции см. в разделе Пространственный поиск.
delaunayTriangulation класс предоставляет другой способ создания триангуляций Delaunay в MATLAB. В то время как delaunay и delaunayTriangulation использовать один и тот же алгоритм и создавать одинаковую триангуляцию, delaunayTriangulation предоставляет дополнительные методы, которые полезны для разработки алгоритмов на основе Delaunay. Эти методы подобны функциям, которые упакованы вместе с данными триангуляции в контейнер, называемый классом. Сохранение всего вместе в классе обеспечивает более организованную настройку, которая повышает удобство использования. Это также повышает производительность поиска на основе триангуляции, такого как местоположение точки и ближайшего соседа. delaunayTriangulation поддерживает инкрементное редактирование триангуляции Делоне. Можно также наложить ограничения кромок в 2-D.
Представления триангуляции вводят triangulation класс, поддерживающий топологические и геометрические запросы для 2-D и 3-D триангуляций. A delaunayTriangulation является особым видом triangulation. Это означает, что вы можете выполнить любое triangulation запрос по delaunayTriangulation в дополнение к специфическим запросам Delaunay. В более формальных терминах языка MATLAB delaunayTriangulation является подклассом triangulation.
В этом примере показано, как создавать, запрашивать и редактировать триангуляцию Delaunay из seamount данные с использованием delaunayTriangulation. Набор данных подводной горы содержит (x, yместа и соответствующие отметки (z), которые определяют поверхность подводной горы.
Загрузить и триангулировать (x, y) данные.
load seamount
DT = delaunayTriangulation(x,y)DT =
delaunayTriangulation with properties:
Points: [294x2 double]
ConnectivityList: [566x3 double]
Constraints: []
Constraints пустое свойство, поскольку нет наложенных граничных ограничений. Points представляет координаты вершин, и ConnectivityList свойство представляет треугольники. Вместе эти два свойства определяют матричные данные для триангуляции.
delaunayTriangulation класс является оберткой вокруг матричных данных и предлагает набор дополнительных методов. Доступ к свойствам в delaunayTriangulation таким же образом осуществляется доступ к полям структуры.
Доступ к данным вершины.
DT.Points;
Доступ к данным подключения.
DT.ConnectivityList;
Доступ к первому треугольнику в ConnectivityList собственность.
DT.ConnectivityList(1,:)
ans = 1×3
205 230 262
delaunayTriangulation обеспечивает простой способ индексации в ConnectivityList матрица свойств.
Доступ к первому треугольнику.
DT(1,:)
ans = 1×3
205 230 262
Проверьте первую вершину первого треугольника.
DT(1,1)
ans = 205
Проверьте все треугольники в триангуляции.
DT(:,:);
Индексирование в delaunayTriangulation вывод, DT, работает как индексирование в массив триангуляции, выводимый из delaunay. Разница между ними заключается в дополнительных методах, которые можно вызвать DT (например, nearestNeighbor и pointLocation).
Использовать triplot для построения графика delaunayTriangulation. triplot функция не является delaunayTriangulation метод, но он принимает и может построить график delaunayTriangulation.
triplot(DT); axis equal xlabel('Longitude'), ylabel('Latitude') grid on

Кроме того, можно использовать triplot(DT(:,:), DT.Points(:,1), DT.Points(:,2)); чтобы получить тот же самый сюжет.
Используйте delaunayTriangulation способ, convexHull, чтобы вычислить выпуклый корпус и добавить его в график. Поскольку триангуляция Делоне уже существует, этот метод позволяет получить выпуклый корпус более эффективно, чем полный расчет с помощью convhull.
hold on k = convexHull(DT); xHull = DT.Points(k,1); yHull = DT.Points(k,2); plot(xHull,yHull,'r','LineWidth',2); hold off

Вы можете инкрементно редактировать delaunayTriangulation для добавления или удаления точек. Если необходимо добавить точки в существующую триангуляцию, то инкрементное добавление выполняется быстрее, чем полное повторное ангулирование набора дополненных точек. Инкрементное удаление точек более эффективно, если количество удаляемых точек мало по сравнению с существующим количеством точек.
Отредактируйте триангуляцию, чтобы удалить точки на выпуклом корпусе из предыдущего расчета.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on % The convex hull topology duplicates the start and end vertex. % Remove the duplicate entry. k(end) = []; % Now remove the points on the convex hull. DT.Points(k,:) = []
DT =
delaunayTriangulation with properties:
Points: [274x2 double]
ConnectivityList: [528x3 double]
Constraints: []
% Plot the new triangulation. hold on triplot(DT); hold off

Есть одна вершина, которая находится как раз внутри границы выпуклого корпуса, который не был удален. Тот факт, что корпус является внутренним, можно увидеть с помощью инструмента «Увеличить» на рисунке. Можно нарисовать метки вершин, чтобы определить индекс этой вершины и удалить ее из триангуляции. Кроме того, можно использовать nearestNeighbor способ более простой идентификации индекса.
Точка близка к месту расположения (211,6, -48,15). Используйте метод nearestNeighbor, чтобы найти ближайшую вершину.
vertexId = nearestNeighbor(DT, 211.6, -48.15)
vertexId = 50
Теперь удалите эту вершину из триангуляции.
DT.Points(vertexId,:) = []
DT =
delaunayTriangulation with properties:
Points: [273x2 double]
ConnectivityList: [525x3 double]
Constraints: []
Постройте график новой триангуляции.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Добавьте точки в существующую триангуляцию. Добавьте 4 точки, чтобы образовать прямоугольник вокруг триангуляции.
Padditional = [210.9 -48.5; 211.6 -48.5; ...
211.6 -47.9; 210.9 -47.9];
DT.Points(end+(1:4),:) = PadditionalDT =
delaunayTriangulation with properties:
Points: [277x2 double]
ConnectivityList: [548x3 double]
Constraints: []
Закройте все существующие фигуры.
close allПостройте график новой триангуляции.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Можно отредактировать точки в триангуляции, чтобы переместить их в новое расположение. Отредактируйте первый из дополнительных наборов точек (идентификатор вершины 274).
DT.Points(274,:) = [211 -48.4];
Закройте все существующие фигуры.
close allПостройте график новой триангуляции
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Используйте метод triangulation класс, vertexAttachments, чтобы найти присоединенные треугольники. Поскольку число треугольников, присоединенных к вершине, является переменным, метод возвращает присоединенные идентификаторы треугольников в массиве ячеек. Вам нужны скобки, чтобы извлечь содержимое.
attTris = vertexAttachments(DT,274); hold on triplot(DT(attTris{:},:),DT.Points(:,1),DT.Points(:,2),'g') hold off

delaunayTriangulation также может использоваться для триангуляции точек в 3-D пространстве. Полученная триангуляция состоит из тетраэдров.
В этом примере показано, как использовать delaunayTriangulation для создания и построения графика триангуляции точек 3-D.
rng('default')
P = rand(30,3);
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [30x3 double]
ConnectivityList: [102x4 double]
Constraints: []
faceColor = [0.6875 0.8750 0.8984]; tetramesh(DT,'FaceColor', faceColor,'FaceAlpha',0.3);

tetramesh функция отображает как внутреннюю, так и внешнюю грани триангуляции. Для больших 3-D триангуляций печать внутренних граней может быть ненужным использованием ресурсов. График границы может быть более подходящим. Вы можете использовать freeBoundary способ получения граничной триангуляции в матричном формате. Затем передайте результат в trimesh или trisurf.
delaunayTriangulation позволяет ограничить ребра в 2-D триангуляции. Это означает, что можно выбрать пару точек в триангуляции и ограничить кромку для соединения этих точек. Это можно представить как «форсирование» кромки между одной или несколькими парами точек. В следующем примере показано, как ограничения кромок могут влиять на триангуляцию.
Триангуляция ниже является триангуляцией Делоне, потому что она уважает критерий пустого окружности.

Триангуляция набора точек с ограничением кромки, заданным между вершинами V1 и V3.
Определите набор точек.
P = [2 4; 6 1; 9 4; 6 7];
Определите ограничение, C, между V1 и V3.
C = [1 3]; DT = delaunayTriangulation(P,C);
Постройте график триангуляции и добавьте аннотации.
triplot(DT) % Label the vertices. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf('V%d', n)}, (1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ... 'bold', 'HorizontalAlignment','center', 'BackgroundColor', ... 'none'); hold off % Use the incenters to find the positions for placing triangle labels on the plot. hold on IC = incenter(DT); numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off % Plot the circumcircle associated with the triangle, T1. hold on [CC,r] = circumcenter(DT); theta = 0:pi/50:2*pi; xunit = r(1)*cos(theta) + CC(1,1); yunit = r(1)*sin(theta) + CC(1,2); plot(xunit,yunit,'g'); axis equal hold off

Ограничение между вершинами (V1, V3) был соблюден, однако критерий Делоне был признан недействительным. Это также делает недействительным отношение ближайший-сосед, которое присуще триангуляции Делоне. Это означает, что nearestNeighbor метод поиска, предоставляемый delaunayTriangulation не может поддерживаться, если триангуляция имеет ограничения.
В типичных применениях триангуляция может состоять из множества точек, и относительно небольшое количество кромок в триангуляции может быть ограничено. Такая триангуляция, как говорят, локально не-Делоне, потому что многие треугольники в триангуляции могут уважать критерий Делоне, но локально могут быть некоторые треугольники, которые делают это. Во многих применениях локальная релаксация свойства пустой окружности не является проблемой.
Ограниченные триангуляции обычно используются для триангуляции неконвексного многоугольника. Зависимости дают нам соответствие между ребрами многоугольника и ребрами триангуляции. Эта связь позволяет извлечь триангуляцию, представляющую область. В следующем примере показано, как использовать ограничение delaunayTriangulation для триангуляции невыпуклого многоугольника.
Определите и постройте график многоугольника.
figure() axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',... 'none','EdgeColor','r'); % Label the points. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf('P%d', n)}, (1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ... 'bold', 'HorizontalAlignment','center', 'BackgroundColor', ... 'none'); hold off

Создайте и постройте график триангуляции вместе с границей многоугольника.
figure() subplot(2,1,1); axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; DT = delaunayTriangulation(P); triplot(DT) hold on; patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',... 'none','EdgeColor','r'); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)

Эту триангуляцию нельзя использовать для представления области многоугольника, поскольку некоторые треугольники пересекают границу. Необходимо наложить ограничение на кромки, которые вырезаются ребрами триангуляции. Поскольку все кромки должны соблюдаться, необходимо ограничить все кромки. Ниже показано, как ограничить все кромки.
Введите определение ограничиваемой кромки. Просмотрите из аннотированного рисунка, где вам нужны зависимости (между (V1, V2), (V2, V3) и так далее).
C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1];
В общем, если есть N точки в последовательности, которые определяют полигональную границу, ограничения могут быть выражены как C = [(1:(N-1))' (2:N)'; N 1];.
Укажите зависимости при создании delaunayTriangulation.
DT = delaunayTriangulation(P,C);
Можно также наложить ограничения на существующую триангуляцию, задав Constraints свойство: DT.Constraints = C;.
Постройте график триангуляции и многоугольника.
figure('Color','white') subplot(2,1,1); axis([-1 17 -1 6]); axis equal triplot(DT) hold on; patch(P(:,1),P(:,2),'-r','LineWidth',2, ... 'FaceColor','none','EdgeColor','r'); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)

График показывает, что кромки триангуляции соответствуют границе многоугольника. Однако триангуляция заполняет вогнутости. Необходима триангуляция, представляющая полигональную область. Можно извлечь треугольники внутри многоугольника с помощью delaunayTriangulation способ, isInterior. Этот метод возвращает логический массив, true и false значения, указывающие, находятся ли треугольники внутри ограниченной геометрической области. Анализ основан на теореме Джордана (Jordan Curve), а границы определяются граничными ограничениями. i-й треугольник в триангуляции считается находящимся внутри области, если i-й логический флаг имеет значение true, в противном случае он находится снаружи.
Теперь используйте isInterior способ вычисления и построения графика набора доменных треугольников.
% Plot the constrained edges in red. figure('Color','white') subplot(2,1,1); plot(P(C'),P(C'+size(P,1)),'-r','LineWidth', 2); axis([-1 17 -1 6]); % Compute the in/out status. IO = isInterior(DT); subplot(2,1,2); hold on; axis([-1 17 -1 6]); % Use triplot to plot the triangles that are inside. % Uses logical indexing and dt(i,j) shorthand % format to access the triangulation. triplot(DT(IO, :),DT.Points(:,1), DT.Points(:,2),'LineWidth', 2) hold off;

Алгоритмы Делоне в MATLAB строят триангуляцию из уникального набора точек. Если точки, переданные функции триангуляции или классу, не уникальны, обнаруживаются повторяющиеся расположения и повторяющаяся точка игнорируется. Это приводит к триангуляции, которая не ссылается на некоторые точки в исходном вводе, а именно на повторяющиеся точки. При работе с delaunay и delaunayn функции, наличие дубликатов может быть незначительным последствием. Однако, поскольку многие из запросов, предоставленных delaunayTriangulation классы основаны на индексах, важно понимать, что delaunayTriangulation триангулирует и работает с уникальным набором данных. Поэтому индексирование на основе уникального набора точек является соглашением. Эти данные ведутся Points имущество delaunayTriangulation.
Следующий пример иллюстрирует важность ссылки на уникальный набор данных, хранящийся в Points свойство при работе с delaunayTriangulation:
rng('default')
P = rand([25 2]);
P(18,:) = P(8,:)
P(16,:) = P(6,:)
P(12,:) = P(2,:)
DT = delaunayTriangulation(P)
Points свойство показывает, что повторяющиеся точки удалены из данных.DT =
delaunayTriangulation with properties:
Points: [22x2 double]
ConnectivityList: [31x3 double]
Constraints: []DT.Points. Поэтому для вычисления и построения графика выпуклого корпуса используйте следующий код:K = DT.convexHull(); plot(DT.Points(:,1),DT.Points(:,2),'.'); hold on plot(DT.Points(K,1),DT.Points(K,2),'-r');
delaunayTriangulation, тогда результат будет неверным. delaunayTriangulation работает с индексами, основанными на уникальном наборе данных DT.Points. Например, следующее приведет к неправильному графику, поскольку K индексируется относительно DT.Points и не P:K = DT.convexHull(); plot(P(:,1),P(:,2),'.'); hold on plot(P(K,1),P(K,2),'-r');
delaunayTriangulation. Это устраняет возможность путаницы. Это может быть выполнено с помощью unique выполнять следующие функции: rng('default') P = rand([25 2]); P(18,:) = P(8,:) P(16,:) = P(6,:) P(12,:) = P(2,:) [~, I, ~] = unique(P,'first','rows'); I = sort(I); P = P(I,:); DT = delaunayTriangulation(P) % The point set is unique