Блокирование манипулируемых переменных является альтернативой более простой концепции горизонта управления (см. Выбор времени выборки и горизонтов) и обладает многими из тех же преимуществ. Блокирование управляемой переменной:
Обеспечивает большую гибкость настройки
Возможность сглаживания регулируемых переменных
Может повысить надежность контроллера
Чтобы использовать блокировку с управляемыми переменными, разделите горизонт прогнозирования на ряд интервалов блокировки, указав горизонт управления как вектор размеров блоков, [m1, m2,...]. Сумма размеров блоков должна соответствовать горизонту прогнозирования p. Если указан вектор, сумма которого равна:
Меньше горизонта прогнозирования, тогда контроллер добавляет интервал блокировки. Длина этого интервала такова, что сумма длин интервала равна р. Например, если p =10 и указывается горизонт управления m =[1 2 3], то контроллер использует четыре интервала с длинами [1 2 3 4].
Больше горизонта прогнозирования, то интервалы усекаются до тех пор, пока сумма длин интервалов не будет равна р. Например, если p =10 и указывается горизонт управления [1 2 3 6 7], то контроллер использует четыре интервала с длинами [1 2 3 4].
Контроллер вычисляет М свободных ходов, где М - количество интервалов блокировки. Первое свободное перемещение применяется к временам k-k + m1-1, второе свободное перемещение применяется от времени k + m1-k + m1 + m2-1 и так далее. Здесь k - текущий интервал управления.
По умолчанию контроллер затем удерживает управляемую переменную константу в каждом блоке; то есть управляющие перемещения являются кусочно постоянными в каждом интервале. Например, на следующем рисунке показаны оптимальные управляющие перемещения для управляющего горизонта m =[2 3 2] и горизонт прогнозирования p =7.
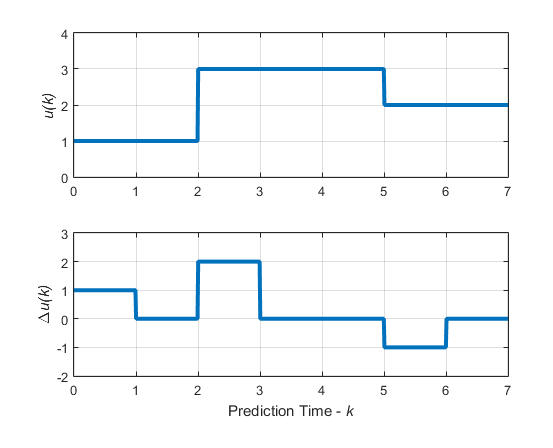
Для каждого блока управляемая переменная u является постоянной, то есть:
u (0) = u (1)
u (2) = u (3) = u (4)
u (5) = u (6)
Рекомендуемый подход к блокированию состоит в разделении горизонта прогнозирования на 3-5 блоков и использовании одной из следующих альтернатив блокирования:
Равные размеры блоков (от одной пятой до одной трети горизонта прогнозирования, p)
Увеличиваются размеры блоков. Например, с p =20, вы можете попробовать три блока с интервалами 3, 7 и 10.
Чтобы проверить влияние различных конфигураций блокировки переменных с манипуляциями, выполните тесты моделирования с замкнутым контуром при следующих условиях:
Без ограничений
Ошибка прогнозирования отсутствует; то есть модель прогнозирования контроллера должна быть идентична модели установки
Чтобы проверить каждый контроллер на устойчивость и надежность, используйте review функция.
Как и в случае с линейным ПДК-контроллером, при использовании регулируемой блокировки переменных нелинейный ПДК-контроллер по умолчанию использует кусочно-постоянные интервалы блокировки. Этот подход часто является слишком ограничительным для приложений оптимального планирования путей. Чтобы создать менее ограничительную проблему нелинейного программирования с лучшими условиями, можно задать кусочно-линейные интервалы блокировки переменных. Для этого установите Optimization.MVInterpolationOrder собственность вашего nlmpc объект контроллера для 1.
На следующем рисунке показаны оптимальные перемещения управления для горизонта управления m =[2 3 2] и горизонт прогнозирования p =7.
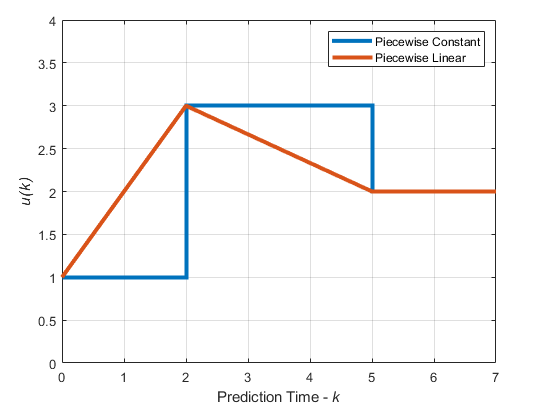
В случае кусочно-постоянной переменной по умолчанию вычисленные манипулируемые значения 1, 3, и 2 являются постоянными на протяжении соответствующих интервалов блокировки.
В кусочно-линейном случае вычисленные значения манипулируемых переменных линейно интерполируются для первых двух блокирующих интервалов и удерживаются постоянными для конечного интервала.
Дополнительные сведения о нелинейных контроллерах MPC см. в разделе Нелинейные MPC.
Примечание
Линейная интерполяция блокирующих перемещений не поддерживается для неявных, адаптивных или запланированных по коэффициенту усиления MPC-контроллеров.