Проблема оптимизации

Обзор

Модельный прогностический контроль решает задачу оптимизации - в частности, квадратичную программу (QP) - на каждом контрольном интервале. Решение определяет управляемые переменные (MV), которые будут использоваться на заводе до следующего интервала управления.

Эта проблема QP включает в себя следующие функции:

Целевая, или «стоимостная», функция - скалярная, неотрицательная мера производительности контроллера, подлежащая минимизации.
Ограничения (Constraints) - условия, которым должно удовлетворять решение, такие как физические границы для MV и выходные переменные установки.
Решение - корректировки MV, которые минимизируют функцию затрат при удовлетворении ограничений.

В следующих разделах эти функции описаны более подробно.

Функция стандартных затрат

Функция стандартных затрат представляет собой сумму четырех терминов, каждый из которых фокусируется на конкретном аспекте производительности контроллера, а именно:

$J (_{} zk)_{=}_{Jy} (_{zk})_{+} {Ju}_{(} {zk}_{)} +_{} {JΔu}_{} ($ zk) + Jλ (zk).

Здесь _zk является решением QP. Как описано ниже, каждый термин включает веса, которые помогают сбалансировать конкурирующие цели. Хотя контроллер MPC предоставляет веса по умолчанию, обычно необходимо настроить их для настройки контроллера для вашего приложения.

Отслеживание ссылки на вывод

В большинстве приложений контроллер должен поддерживать выбранные выходы установки на уровне или вблизи заданных контрольных значений. Контроллер MPC использует следующую скалярную меру производительности для отслеживания опорного сигнала вывода:

$_{Jy} (_{} zk)_{}^{_{}} =∑j=1ny_{}^{} {\frac{_{}^{}}{_{}^{}}_{} \sumi=1p{wi,jysjy[rj (k + i |_{} k) - yj (k}^{} +$ i | k)]} 2.

Здесь,

k - Интервал текущего управления.
p - Горизонт прогнозирования (количество интервалов).
_ny - количество выходных переменных установки.
_zk - решение QP, данное:
$_{}^{zkT} = \begin{matrix} {[u (}^{} & k 'k {) Ту (k}^{} & + & {1 | k)}^{T⋯u} & _{(} \end{matrix} k$ + p − 1 | k) Т.k].
_yj (k + i 'k) - прогнозируемое значение выхода j-ой установки на i-ом шаге горизонта прогнозирования, в инженерных единицах.
_rj (k + i 'k) - Опорное значение для выхода j-ой установки на i-ом шаге горизонта прогнозирования, в инженерных единицах.
$_{}^{sjy}$ - Масштабный коэффициент для j-ой установки, в инженерных установках.
$_{wi,}^{}$ jy - Вес настройки для выхода j-ой установки на i-ом шаге горизонта прогнозирования (безразмерный).

Значения _ny, p, $_{}^{sjy}$ и $_{wi,}^{}$ jy являются постоянными спецификациями контроллера. Контроллер принимает опорные значения _rj (k + i 'k) для всего горизонта прогнозирования. Контроллер использует наблюдателя состояния для прогнозирования _{выходов} установки, yj (k + i 'k), которые зависят от регулируемых переменных _{регулировок} (zk), измеренных возмущений (MD) и оценок состояния. На интервале k доступны оценки состояния контроллера и значения MD. _{Поэтому} Jy является _{функцией} только zk.

Отслеживание манипулируемых переменных

В некоторых приложениях, например, при наличии большего количества управляемых переменных, чем выходов установки, контроллер должен поддерживать выбранные управляемые переменные (MV) на уровне или вблизи заданных целевых значений. Контроллер MPC использует следующую скалярную меру производительности для управляемого отслеживания переменных:

$_{Ju} (_{} zk)_{}^{_{}}_{}^{} {\frac{_{}^{}}{_{}^{}}_{} =∑j=1nu∑i=0p−1{wi,jusju[uj (k + i_{| k) -} uj, мишень}^{(} k$ + i | k)]} 2.

Здесь,

k - Интервал текущего управления.
p - Горизонт прогнозирования (количество интервалов).
_nu - количество манипулируемых переменных.
_zk - решение QP, данное:
$_{}^{zkT} = \begin{matrix} {[u (}^{} & k 'k {) Ту (k}^{} & + & {1 | k)}^{T⋯u} & _{(} \end{matrix} k$ + p − 1 | k) Т.k].
_{uj, цель} (k + i 'k) - целевое значение для j-го СН на i-ом шаге горизонта прогнозирования, в инженерных единицах.
$_{}^{sju}$ - Масштабный коэффициент для j-го СН, в инженерных установках.
$_{wi,}^{}$ ju - вес настройки для jth MV на i-ом шаге горизонта прогнозирования (безразмерный).

Значения _nu, p, $_{}^{sju}$ и $_{wi,}^{}$ ju являются постоянными спецификациями контроллера. Контроллер принимает значения _{uj, target} (k + i 'k) для всего горизонта. Контроллер использует наблюдателя состояния для прогнозирования выходов установки. _{Таким образом}, Ju является функцией только zk.

Подавление перемещения манипулируемой переменной

Большинство приложений предпочитают небольшие регулировки СН (перемещения). Константа MPC использует следующую скалярную меру производительности для управляемого подавления перемещения переменных:

$_{JΔu} (_{} zk)_{}^{_{}} {=\sumj=1nu}_{}^{} {\frac{_{}^{}}{_{}^{}}_{} ∑i=0p−1{wi,jΔusju[uj (k + i_{|} k) - uj (k}^{+}$ i − 1 | k)]} 2.

Здесь,

k - Интервал текущего управления.
p - Горизонт прогнозирования (количество интервалов).
_nu - количество манипулируемых переменных.
_zk - решение QP, данное:
$_{}^{zkT} = \begin{matrix} {[u (}^{} & k 'k {) Ту (k}^{} & + & {1 | k)}^{T⋯u} & _{(} \end{matrix} k$ + p − 1 | k) Т.k].
$_{}^{sju}$ - Масштабный коэффициент для j-го СН, в инженерных установках.
$_{wi,}^{}$ jΔu - настроечный вес для j-го движения СН на i-ом шаге горизонта прогнозирования (безразмерный).

Значения _nu, p, $_{}^{sju}$ и $_{wi,}^{}$ jΔu являются постоянными спецификациями контроллера. u (k-1 | k) = u (k-1), которые являются известными MV из предыдущего _{интервала} управления. JΔu является функцией только zk.

Кроме того, горизонт управления m < p (или блокировка СН) ограничивает определенные перемещения СН до нуля.

Нарушение ограничения

На практике нарушения ограничений могут быть неизбежными. Мягкие ограничения позволяют реализовать решение QP в таких условиях. В MPC-контроллере используется безразмерная, неотрицательная переменная слабого состояния, _αk, которая количественно определяет наихудшее нарушение ограничения. (См. раздел Ограничения) Соответствующий показатель производительности:

$_{Дже} (_{} зк)_{=}_{}^{}$ αεk2.

Здесь,

_zk - решение QP, данное:
$_{}^{zkT} = \begin{matrix} {[u (}^{} & k 'k {) Ту (k}^{} & + & {1 | k)}^{T⋯u} & _{(} \end{matrix} k$ + p − 1 | k) Т.k].
_αk - Переменная провисания на контрольном интервале k (безразмерный).
_start, - вес штрафа за нарушение ограничения (безразмерный).

Функция альтернативных затрат

Можно использовать следующую альтернативу функции стандартных затрат:

$J (_{} zk)_{}^{} =\sumi=0p-1_{{}^{[} eyT (k_{+} i) Qey (_{k}^{} + i)]_{+}_{[} euT (k + i^{)} Rueu_{(k} + i)] + [_{} {ΔuT}_{}^{(} k$ + i) RΔuΔu (k + i)]} +ρϵεk2.

Здесь Q (_ny-by-ny), _Ru и _RΔu (_nu-by-nu) являются положительными полуопределёнными весовыми матрицами, и:

$\begin{matrix} _{ey} (i + k_{)}^{=} Sy - 1 [r (k + i + 1 | \\ _{k}) - y (_{k}^{+} i_{+ 1 |} k)] eu (i + k) = \\ Su - 1 [_{}^{} utarget (k + i 'k) - u (k \end{matrix}$ + i' k)] Δu (k + i) = Su − 1 [u (k + i 'k) − u (k + i − 1 |

Также,

_Sy - Диагональная матрица масштабных коэффициентов выходных переменных установки, в технических единицах.
_Su - Диагональная матрица масштабных коэффициентов СН в инженерных единицах.
r (k + 1 | k₎ - выходные опорные значения установки на i-м шаге горизонта прогнозирования, в инженерных единицах.
y (k + 1 | k₎ - выходы установки на i-ом шаге горизонта прогнозирования, в инженерных единицах.
_zk - решение QP, данное:
$_{}^{zkT} = \begin{matrix} {[u (}^{} & k 'k {) Ту (k}^{} & + & {1 | k)}^{T⋯u} & _{(} \end{matrix} k$ + p − 1 | k) Т.k].
_utarget (k + i 'k) _- целевые значения nu MV, соответствующие u (k + i' k), в инженерных установках.

В прогнозах вывода используется наблюдатель состояния, как в функции стандартных затрат.

Функция альтернативной стоимости допускает недиагональное взвешивание, но требует, чтобы веса были идентичными на каждом шаге горизонта прогнозирования.

Функции альтернативных и стандартных затрат идентичны, если выполняются следующие условия:

Функции стандартной стоимости используют веса $_{wi,}^{}$ jy, $_{wi,}^{}$ ju $и_{wi}^{,}$ jΔu, которые являются постоянными по отношению к индексу, i = 1: p.
Матрицы Q, _Ru и _RΔu являются диагональными с квадратами этих весов в качестве диагональных элементов.

Ограничения

Некоторые ограничения неявны. Например, горизонт управления m < p (или блокировка MV) заставляет некоторые приращения MV быть нулевыми, и наблюдатель состояния, используемый для прогнозирования выхода установки, представляет собой набор неявных ограничений равенства. Явные ограничения, которые можно настроить, описаны ниже.

Границы на выходах завода, MV и приращения MV

Наиболее распространенными ограничениями MPC являются границы, как показано ниже.

$\begin{matrix} \frac{_{yj, минута}}{{(i)}_{}^{}}_{}_{sjy−εkVj,}^{} miny \frac{_{(i)} ≤yj}{_{}^{}} \frac{{(k+i'k)}_{} sjy≤yj,}{_{}^{макс.}}_{} {(i)}_{}^{} sjy +εkVj, maxy (i), i=1:p,_{} \\ \frac{_{j=1:nyuj},}{{минута}_{}^{}} {(i)}_{}_{}^{} sju-εkVj, \frac{_{minu} (i) ≤uj}{_{}^{}} \frac{_{(k+i−1|k)}}{_{}^{sju≤uj}},_{} {макс.}_{(i)}^{} sju +εkVj, maxu (i),_{} \\ \frac{i=1:p,_{}}{_{j=1:nuΔuj}^{,}}_{минута}_{(i)}^{} \frac{sju−εkVj,_{} minΔu (i)}{\leq_{}^{}} Δuj \frac{_{} (k+i-1|k)}{_{}^{}} sju_{}_{≤Δuj, макс.}^{} (i) sju +εkVj, maxΔu {(i)}_{,} \end{matrix}$ i=1:p, j=1:nu.

Здесь параметры V (значения ECR) являются константами контроллера без размерности, аналогичными весам функции затрат, но используемыми для смягчения ограничений (см. Смягчение ограничений). Также,

_αk - скалярная переменная ослабления QP (безразмерная), используемая для смягчения ограничения.
$_{}^{sjy}$ - Масштабный коэффициент для j-ой установки, в инженерных установках.
$_{}^{sju}$ - Масштабный коэффициент для j-го СН, в инженерных установках.
yj_{, min} (i), _yj, max (i) - нижняя и верхняя границы для выхода j-ой установки на i-ом шаге горизонта прогнозирования, в инженерных единицах.
uj_{, min} (i), _uj, max (i) - нижние и верхние границы для j-го СН на i-ом шаге горизонта прогнозирования, в инженерных установках.
Δuj_{, мин} (i), _Δuj, макс (i) - нижняя и верхняя границы для приращения j-го СН на i-м шаге горизонта прогнозирования, в инженерных единицах.

За исключением условия non-negativity переменной проволочек, все вышеперечисленные ограничения являются необязательными и по умолчанию неактивны (т.е. инициализированы с бесконечными ограничивающими значениями). Чтобы включить ограничение границы, необходимо указать конечный предел при проектировании контроллера.

Матрицы QP

В этом разделе описываются матрицы, связанные с задачей оптимизации управления с предсказанием модели, описанной в разделе Задача оптимизации.

Прогноз

Предположим, что модели возмущений, описанные во входной модели возмущений, представляют собой единичные коэффициенты усиления; то есть d (k) = _nd (k) - белый гауссов шум. Эту проблему можно обозначить как

$x \leftarrow \begin{matrix} _{} \end{matrix} [xxd], \begin{matrix} _{} \overset{}{} \\ \overset{}{} \end{matrix} \leftarrow[ABdC¯0A¯],_{} \begin{matrix} _{} \end{matrix} Бу [Bu0],_{} \begin{matrix} \end{matrix} Bv [Bv0],_{} \begin{matrix} _{} \overset{}{} \\ \overset{}{} \end{matrix} BD [BdDюBю], \begin{matrix} _{} \overset{C [CDdCю}{} \end{matrix}]$

Затем модель прогнозирования представляет собой:

x (k + 1) = Ax (k₎ + Buu ₍k) + _Bvv (k) + Bdnd (k)

y (k) = Cx (k) ₊ Dvv (k₎ ₊ Ddnd (k)

Далее рассмотрим задачу прогнозирования будущих траекторий модели, выполняемых в момент времени k = 0. Установить nd (i) = 0 для всех моментов прогнозирования i и получить

$y (i | 0)^{=} C [_{Aix (}^{0)}^{}_{} +∑h=0i−1Ai−1 (_{Bu (}^{u} (- 1)_{} +\sumj=0hΔu (_{j})) +$ Bvv (h)] + Dvv (i)

Это уравнение дает решение

$[\begin{matrix} y (1 \\ ) \\ ⋯y \end{matrix} (p)_{]} = {Sxx}_{(} 0) +_{} Su1u \begin{matrix} (- 1 \\ ) \\ + Su [ \end{matrix} Δu_{(} 0 \begin{matrix} ) \\ \dotsΔu \\ (p \end{matrix} -$ 1)] + Hv [v (0) ⋯v (p)]

где

$\begin{array}{l} _{Sx} = \begin{matrix} ^{} \\ ^{} \end{matrix}^{_{}_{[CACA2CAp] pny×nx}},_{} \begin{matrix} _{} \\ _{}_{} \\ _{}^{}^{}_{} \end{matrix}^{_{}_{}} \\ _{} \begin{matrix} _{} \\ _{}_{} & _{} \\ _{}^{}^{}_{} & _{}^{}^{}_{} & _{} \end{matrix}^{_{}_{}} \\ _{} \begin{matrix} _{} & _{} \\ _{} & _{} & _{} \\ ^{}_{} & ^{}_{} & ^{}_{} & _{} \end{matrix}^{_{} Su1=[CBuCBu+CABu\dots\sumh=0p-1CAhBu]\inℜpny\timesnuSu=[CBu0\dots0CBu+CABuCBu\dots0\dots\dots\dots\dots\sumh=0p-1CAhBu\sumh=0p-2CAhBu\dotsCBu]\inℜpny\timespnuHv=[CBvDv0\dots0CABvCBvDv\dots0\dots\dots\dots\dots\dotsCAp-1BvCAp-2BvCAp-3Bv\dotsDv]\inℜpny\times {(p+1)}_{}} \end{array}$ nv.

Переменные оптимизации

Пусть m - число перемещений свободного управления, и пусть z = [_z0;...; zm-1]. Затем,

$[\begin{matrix} Δu (0 \\ ) \\ ⋯Δu (p \end{matrix} -_{1}) \begin{matrix} ]_{} \\ _{} \end{matrix}$ =JM[z0⋯zm−1]

где JM зависит от выбора блокирующих ходов. Вместе с переменной слабости ɛ векторы z0,..., zm-1 составляют свободные переменные оптимизации задачи оптимизации. В случае систем с одной манипулируемой переменной, z0_,..., zm-1 _{являются} скалярами.

Рассмотрим блокирующие движения, показанные на следующем графике.

Блокирование перемещений: входные и входные приращения для перемещений = [2 3 2]

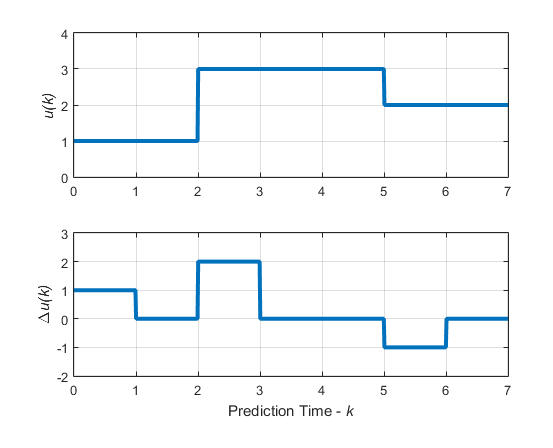
Этот график соответствует выбору moves=[2 3 2], или эквивалентно, u (0) = u (1), u (2) = u (3) = u (4), u (5) = u (6), Δ u (0) = z0, Δ u (2) = z1, Δ u (5) = z2, Δ u (1) = Δ u (3) = Δ u (4) = Δ u (6) = 0

Затем соответствующей матрицей _JM является

$_{JM} = \begin{matrix} [I000000I000000000I000 \end{matrix}]$

Дополнительные сведения о блокировании манипулируемых переменных см. в разделе Блокирование манипулируемых переменных.

Функция затрат

Стандартная форма. Оптимизируемая функция:

$\begin{array}{l} J (z, ε) {= \begin{matrix} ([u \\ (0) \dotsu \end{matrix} \begin{matrix} _{(p−1)] - [} \\ _{utarget (0)} \end{matrix}}^{} {⋯utarget}_{}^{} \begin{matrix} (p-1)] \\ ) \\ TWu2 \end{matrix} ([u \begin{matrix} _{(0) ⋯u} \\ _{(p−1)] - [} \end{matrix} utarget {\begin{matrix} (0) \\ ⋯utarget \end{matrix}}^{} {(p−1)}_{]}^{)} \begin{matrix} + [Δu \\ (0) \dots Δu \end{matrix} \\ (p−1) ] TWΔu2 [{Δu \begin{matrix} (0) \\ \dots Δu \end{matrix} \begin{matrix} (p-1)] \\ + ([ \end{matrix} y}^{}_{(1)}^{} \dotsy \begin{matrix} (p) \\ ] - [r \end{matrix} \begin{matrix} (1) \dotsr \\ (p) \end{matrix}])_{}^{TWy2} \end{array}$ ([y (1) ⋯y (p)] − [r (1) ⋯r (p)]) + ρεε2

где

\begin{matrix} _{Wu} = {diag}_{(}^{}_{w0,1u,}^{} w0,2u, ._{. .,_{}}^{} w0, {nuu}_{, . . .,}^{} {wp}_{-}^{} 1,1u, wp_{-_{1,2u}}^{,} . \\ ._{.,} wp − 1_{,}^{nuu})_{WΔu}^{=} diag_{(_{}}^{} w0,1Δu,_{w0,2Δu, .}^{. .},_{w0,}^{} nuΔu,.. .,_{wp -_{}}^{} \\ _{1,1Δu}_{}^{}_{}^{}_{_{}}^{}_{}^{}_{}^{}_{_{}}^{} \end{matrix}

(1)

Наконец, после замены u (k) Δu (k), y (k), J (z) могут быть переписаны как

\begin{array}{l} J (z, start)_{} =^{}^{} {αα2}_{+} {\begin{matrix} zTKΔuz + \\ 2 ([ \end{matrix} r}^{} (_{1}) {\begin{matrix} \dotsr ( \\ p \\ )] \end{matrix}}^{TKr}_{+} [{v (0}^{)}_{} \dotsv {\begin{matrix} (_{p)]} TKv + \\ u_{(- 1)} TKu \end{matrix} +}^{} [_{} {utarget}^{} (_{0}) \\ ⋯utarget  ( p -_{}^{1})_{]}_{}_{TKut}^{} +_{} x_{} \end{array}

(0) TKx)

(2)

где

$\begin{array}{l} _{cy} =_{} Sxx (0_{)} + Su1u_{(} - \begin{matrix} 1) \\ + \\ Hv \end{matrix} [v \begin{matrix} (0) \\ ⋯v (p \end{matrix}) \\ ]_{} - \begin{matrix} [_{r} \\ (_{1} \end{matrix}) \dotsr (p) \begin{matrix} ]_{} \\ _{cu=[I1⋯Ip]u (- 1}) - [ \end{matrix} \end{array}$ utarget (0) ⋯utarget (p − 1)]

Здесь I1 =... = _Ip - это единичные матрицы размера _nu.

Примечание

Возможно, проблема QP останется строго выпуклой. Если номер условия гессенской матрицы _KΔU больше ¹⁰¹², добавьте количество 10*sqrt(eps) на каждом диагональном члене. Это решение можно использовать только в том случае, если все входные скорости не enalized (^WΔu = 0) (см. Weights имущества mpc объект).

Функция альтернативных затрат. При использовании функции альтернативных затрат, показанной в разделе Функция альтернативных затрат, уравнение 1 заменяется следующим:

\begin{array}{l} _{Wu} = {blkdiag}_{} (Ru, . ._{.}, \\ _{Ru}) WΔu =_{} blkdiag (_{RΔu}, \\ ._{.} ., RΔu) Wy = \end{array}

blkdiag (Q,..., Q)

(3)

В этом случае блочно-диагональные матрицы повторяют p раз, например, один раз для каждого шага в горизонте прогнозирования.

Также можно использовать комбинацию стандартных и альтернативных форм. Дополнительные сведения см. в разделе Weights имущества mpc объект.

Ограничения

Далее рассмотрим ограничения на входы, приращения ввода и выходы вместе с ограничением ɛ≥ 0.

$[\begin{matrix} _{ymin} (1)_{}^{} −εVminy \\ _{(1)} \dotsymin_{(p)}^{} \\ _{−εVminy} (p)_{umin}^{} (0) \\ _{} −εVminu (0)_{}^{⋯umin} \\ (p−1)_{} -εVminu_{}^{(p−1)} \\ Δumin_{(0)}_{−εVminΔu}^{(0)} \dots \end{matrix} Δumin \begin{matrix} (p-1) \\ -εVminΔu \\ (p-1) \\ ] \leq [y \\ (1) ⋯y \end{matrix} (p) \begin{matrix} _{u} (0) ⋯u_{}^{} (p-1) \\ Δu \\ _{(0)} \dots Δu_{}^{(p−1)}] \leq \\ [_{} ymax (1)_{+}^{} εVmaxy \\ _{(1)} \dotsymax_{(p) +}^{} εVmaxy \\ _{(p)} umax_{(0)}^{+} \\ εVmaxu_{(0)} \dotsumax_{}^{(p−1)} + \end{matrix}$ εVmaxu (p−1) Δumax (0) + εVmaxΔu (0) ⋯ Δumax (p−1) + εVmaxΔu (p−1)]

Примечание

Чтобы уменьшить вычислительные усилия, контроллер автоматически устраняет посторонние ограничения, такие как бесконечные границы. Таким образом, набор ограничений, используемый в реальном времени, может быть намного меньше, чем тот, который предлагается в этом разделе.

Аналогично тому, что вы сделали для функции затрат, вы можете заменить u (k), Δu (k), y (k) и получить

_{}_{}_{}_{} \begin{matrix} Mzz+Mεε≤Mlim+Mv[v (0 \\ ) \\ ⋯v \end{matrix} (p)_{]} + Муу_{(} - 1)

+ Mxx (0)

(4)

В этом случае матрицы _Mz, Mɛ, Mlim, _Mv, _Mu и _Mx получают из верхней и нижней границ и значений ECR.

Неограниченный предиктивный контроль модели

Оптимальное решение вычисляется аналитически

$z * =_{-}^{} {KΔu \begin{matrix} - 1 \\ ([r \end{matrix} (}^{1})_{} \dotsr \begin{matrix} (p) \\ ] \\ TKr \end{matrix} +_{} [v {(0)}^{}_{⋯v} {(\begin{matrix} p_{)] Kv} + u \\ (_{- 1)} TKu + \end{matrix} [}^{}_{} {utarget (}^{0})_{}^{}$ ⋯utarget (p − 1)] TKut + x (0) TKx) T

и модельный прогнозирующий контроллер устанавливает Δu (k) = z * 0, u (k) = u (k-1) + Δu (k).

Документация