По умолчанию при создании объекта контроллера с помощью mpc команда, зависимости отсутствуют. Чтобы включить ограничение, задайте соответствующее свойство контроллера. В следующей таблице представлены свойства контроллера, используемые для определения большинства ограничений MPC. (MV = переменная, управляемая растением; OV = выходная переменная установки; Приращение MV = u (k) - u (k-1).
| Ограничение | Свойство контроллера | Смягчение зависимостей |
|---|---|---|
| Нижняя граница на i-ом СН | MV(i).Min > -Inf | MV(i).MinECR > 0 |
| Верхняя граница на i-ом СН | MV(i).Max < Inf | MV(i).MaxECR > 0 |
| Нижняя граница на i-ом OV | OV(i).Min > -Inf | OV(i).MinECR > 0 |
| Верхняя граница на i-ом OV | OV(i).Max < Inf | OV(i).MaxECR > 0 |
| Нижняя граница на i-ом приращении СН | MV(i).RateMin > -Inf | MV(i).RateMinECR > 0 |
| Верхняя граница на i-ом приращении СН | MV(i).RateMax < Inf | MV(i).RateMaxECR > 0 |
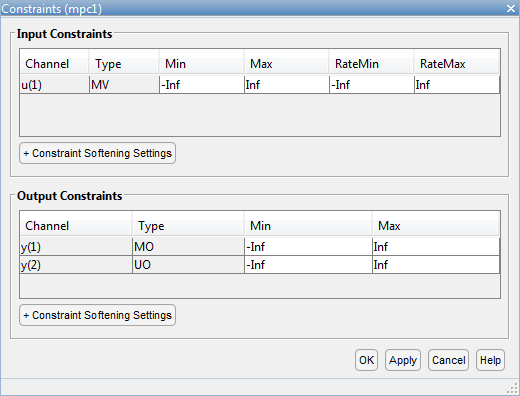
Чтобы задать свойства ограничения контроллера с помощью приложения MPC Designer, на вкладке Настройка щелкните Ограничения.
В ![]() диалоговом окне «Зависимости» задайте значения зависимостей.
диалоговом окне «Зависимости» задайте значения зависимостей.
Уравнения, описывающие соответствующие ограничения, см. в разделе Ограничения.
Для границ СН:
Включить известные физические ограничения на MV завода в качестве жестких границ MV.
Включите ограничения приращения среднего напряжения, если существует известный физический предел скорости изменения, или приложение требует предотвратить большие приращения по какой-либо другой причине.
Не включайте жесткие границы СН и жесткие границы приращения СН на одном и том же СН, поскольку они могут конфликтовать. Если важны оба типа границ, смягчите одну.
Для границ OV:
Не включайте границы OV, если они не являются существенными для вашего приложения. В качестве альтернативы установке границы OV можно определить ссылку на OV и установить ее вес функции затрат, чтобы поддерживать OV близко к ее уставке.
Все ограничения OV должны быть смягчены.
Рассмотрите возможность оставить OV без ограничений для некоторых шагов горизонта прогнозирования. См. раздел Изменяющиеся во времени веса и ограничения.
Рассмотрим изменяющееся во времени ограничение OV, которое легко удовлетворить в начале горизонта, постепенно сужаясь к более строгому ограничению. См. раздел Изменяющиеся во времени веса и ограничения.
Не включайте ограничения OV, которые невозможно удовлетворить. Даже если они мягкие, такие ограничения могут вызвать неожиданное поведение контроллера. Например, рассмотрим установку SISO с пятью периодами задержки отбора проб. Ограничение OV перед шестым шагом горизонта прогнозирования, в общем, невозможно удовлетворить. Вы можете использовать review для проверки таких невозможных ограничений и использования изменяющейся во времени границы OV. См. раздел Изменяющиеся во времени веса и ограничения.
Жесткие ограничения - это ограничения, которые должно удовлетворять решение квадратичного программирования (QP). Если математически невозможно удовлетворить жесткое ограничение на данном интервале управления, k, QP неосуществим. В этом случае контроллер возвращает состояние ошибки и устанавливает управляемые переменные (MV) в u (k) = u (k-1), то есть без изменений. Если условие, приводящее к несходимости, не устранено, несходимость может продолжаться бесконечно долго, что приводит к потере контроля.
Нарушения и ошибки прогнозирования неизбежны на практике. Следовательно, нарушение ограничений может произойти на заводе, даже если контроллер прогнозирует иное. Выполнимое решение QP не гарантирует, что все жесткие ограничения будут удовлетворены при использовании оптимального среднего напряжения на установке.
Если единственными ограничениями в приложении являются ограничения на MV, ограничения MV могут быть жесткими ограничениями, как по умолчанию. Ограничения среднего напряжения сами по себе не могут привести к несходимости. То же самое справедливо, если только ограничения связаны с приращениями СН.
Однако жесткая MV-граница с жестким ограничением приращения MV может привести к несходимости. Например, нарушение или работа при ручном управлении может привести к тому, что фактический СН, используемый на установке, превысит заданный предел во время интервала k-1. Если контроллер находится в автоматическом режиме в течение интервала k, он должен возвратить MV к значению в пределах жесткой границы. Если MV превышает ограничение на слишком большую величину, жесткое ограничение приращения может сделать невозможной коррекцию связанного нарушения в следующем интервале.
Если установка подвержена возмущениям и существуют либо жесткие ограничения на выпуск, либо жесткие ограничения на ввод-вывод, то несходимость QP является явной возможностью.
Все ограничения Toolbox™ предиктивного контроля модели (за исключением переменной слабости nonnegativity) могут быть мягкими. Когда ограничение является мягким, контроллер может считать MV оптимальным, даже если он предсказывает нарушение этого ограничения. Если все выходные данные завода, приращение среднего напряжения и пользовательские ограничения являются мягкими (как по умолчанию), несходимость QP не возникает. Однако производительность контроллера может быть некондиционной.
Чтобы смягчить ограничение, установите соответствующее значение равенства для релаксации (ECR) в положительное значение (ноль подразумевает жесткое ограничение). Чем больше значение ECR, тем больше вероятность того, что контроллер сочтет оптимальным нарушить ограничение, чтобы удовлетворить другие цели производительности. Программное обеспечение Model Predictive Control Toolbox предоставляет значения ECR по умолчанию, но, что касается весов функции затрат, может потребоваться настроить значения ECR для достижения приемлемой производительности.
Чтобы понять, как работает смягчение ограничений, предположим, что функция затрат использует jΔu = 0, давая как MV, так и MV приращение нулевого веса в функции затрат. Только условия отслеживания выходных ссылок и нарушения ограничений не равны нулю. В этом случае функция затрат:
k)]} 2 + ααk2.
Предположим, что вы также указали жесткие границы MV с = 0 (i) = 0. Затем эти ограничения упрощаются для:
p, j = 1: nu.
Таким образом, в вышеприведенных уравнениях больше не фигурирует переменная провисания, αk. Также определены мягкие ограничения на выходы установки с > 0 (i) > 0.
i = 1: p, j = 1: ny.
Теперь предположим, что нарушение выдвинуло производительность установки выше ее указанной верхней границы, но QP с жесткими ограничениями производительности будет осуществимым, то есть все нарушения ограничений можно избежать в решении QP. QP предполагает компромисс между отслеживанием выходных данных и нарушением ограничений. Переменная «slack», αk, должна быть неотрицательной. Его появление в функции стоимости отбивает, но не препятствует, оптимальному αk > 0. Но больший вес, тем не менее, увеличивает вероятность того, что оптимальный δ k будет небольшим или нулевым.
Если оптимальный αk > 0, по крайней мере одно из связанных неравенств должно быть активным (при равенстве). Относительно большое i) облегчает удовлетворение ограничения с маленьким δ k. В этом случае
) sjy
может быть больше, без превышения
maxy (i).
Обратите внимание, что i) не устанавливает верхний предел нарушения ограничения. Скорее, это фактор настройки, определяющий, легко или трудно удовлетворить мягкое ограничение.
Использование безразмерных переменных упрощает настройку ограничений. Определите соответствующие масштабные коэффициенты для каждой входной и выходной переменной установки. См. раздел Определение масштабных коэффициентов.
Чтобы указать относительную величину допустимого нарушения, используйте параметр ECR, связанный с каждым ограничением. Ниже приводятся приблизительные руководящие принципы:
0 - Нарушение не допускается (жесткое ограничение)
0,05 - Допускается очень небольшое нарушение (почти жесткое)
0.2 - Допущено небольшое нарушение (довольно жесткое)
1 - средняя мягкость
5 - допускается нарушение, превышающее среднее (достаточно мягкое)
20 - допускается большое нарушение (очень мягкое)
Используйте общий параметр смягчения ограничения контроллера (свойство объекта контроллера: Weights.ECR), чтобы наказать допустимое нарушение мягкого ограничения относительно других терминов функции затрат. Установите Weights.ECR такое свойство, что соответствующий штраф на 1-2 порядка больше, чем типичная сумма трех других членов функции затрат. Если во время тестов моделирования нарушения ограничений кажутся слишком большими, попробуйте увеличить Weights.ECR в 2-5 раза.
Однако имейте в виду, что чрезмерно большой Weights.ECR искажает оптимизацию СН, приводя к неправильным корректировкам СН при возникновении нарушений ограничений. Чтобы проверить это, просмотрите значение функции затрат во время моделирования. Если его величина увеличивается более чем на 2 порядка при нарушении ограничения, рассмотрите возможность уменьшения Weights.ECR.
Нарушения и ошибки прогнозирования могут привести к неожиданным нарушениям ограничений в реальной системе. Попытки предотвратить эти нарушения путем усложнения ограничений часто ухудшают производительность контроллера.