Алгоритмы многообъективной оптимизации

Определение многообъективной оптимизации

Существует два мультиобъективных решателя Optimization Toolbox™: fgoalattain и fminimax.

fgoalattain решает проблему уменьшения набора нелинейных функций _Fi (x) ниже набора целей F * i. Поскольку существует несколько _{функций} Fi (x), не всегда ясно, что это означает для решения этой задачи, особенно когда вы не можете достичь всех целей одновременно. Поэтому проблема преобразуется в проблему, которая всегда хорошо определена.
Не масштабированная задача достижения цели заключается в минимизации максимума _Fi (x ) - F * i.
Существует полезное обобщение нескрупулезной проблемы. Учитывая набор положительных весов _wi, задача достижения цели пытается найти x, чтобы минимизировать максимум
$\frac{_{Fi} (x)_{-}^{}}{_{Fi}}$ * wi. (1)
Предполагается, что эта минимизация выполняется при удовлетворении всех типов ограничений: c (x ) ≤ 0, ceq ( x) = 0, A · x ≤ b, Aeq · x = beq и l ≤ x ≤ u.
Если установить все веса равными 1 (или любой другой положительной константе), задача достижения цели будет такой же, как и задача достижения цели без масштаба. Если F _* i положительны, и вы устанавливаете все веса как wi = _F * i, задача достижения цели сводится к минимуму относительную разницу между _{функциями} Fi (x) и _целями F * i.
Другими словами, задача достижения цели заключается в минимизации переменной ослабления γ, определяемой как максимум над i выражений в уравнении 1. Это подразумевает выражение, которое является формальным изложением проблемы достижения цели:
$\underset{minx,}{}$ γ γ
так, что F (x ) - w· γ ≤ F *, c ( x) ≤ 0, ceq (x) = 0 , A· x ≤ b, Aeq· x = beq и l ≤ x ≤ u.
fminimax решает проблему минимизации максимума набора нелинейных функций с учетом всех типов ограничений:
$\underset{}{} \underset{}{}_{minxmaxiFi} (x$ )
так, что c (x ) ≤ 0, ceq ( x) = 0, A · x ≤ b, Aeq · x = beq и l ≤ x ≤ u.
Ясно, что эта проблема является частным случаем задачи достижения цели, с F _* i = 0 и wi = 1.

Алгоритмы

Метод достижения цели

В этом разделе описывается метод достижения цели Гембицки [3]. Этот метод использует набор целей проектирования, $F^{} * =_{}^{{} {F1}_{}^{} *, F2_{}^{}$ *,..., Fm *}, связанных с набором целей, F (x) = {F1 (x), _F2 (x),..., Fm (x)}. Формулировка проблемы позволяет недо- или недостичь цели, позволяя конструктору быть относительно неточным относительно первоначальных целей конструкции. Относительная степень недо- или недостижения целей управляется вектором весовых коэффициентов w ₌ {w1, w2,..., wm} и выражается как стандартная задача оптимизации с использованием формулировки.

\underset{minimizeγ∈ℜ,}{} x∈Ωγ

(2)

так, что $_{Fi} (x)_{}_{}^{} -wiγ\leqFi *, i = 1, . .$ ., m.

Термин _wiγ вводит в проблему элемент слабости, который иначе навязывает, чтобы цели были жестко достигнуты. Вектор взвешивания w позволяет проектировщику выразить величину относительных компромиссов между целями. Например, установка вектора w взвешивания равным начальным целям указывает, что достигается тот же процент недо- или недостижения целей, F *. Можно включить жесткие ограничения в конструкцию, установив определенный весовой коэффициент равным нулю (т.е. _wi = 0). Метод достижения цели обеспечивает удобную интуитивную интерпретацию задачи проектирования, которую можно решить с помощью стандартных процедур оптимизации. Иллюстративные примеры использования метода достижения цели при проектировании системы управления можно найти во Флеминге ([10] и [11 ]).

Способ достижения цели представлен геометрически на рисунке ниже в двух измерениях.

Рис. 7-1, Геометрическое представление метода достижения цели

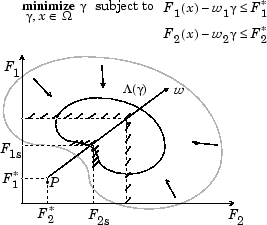
Спецификация целей, ${_{F1}^{} {*,}_{}^{} F2$ *}, определяет точку цели, P. Вектор взвешивания определяет направление поиска от P к возможному функциональному пространству Λ (γ). Во время оптимизации γ изменяется, что изменяет размер возможной области. Границы зависимости сходятся к уникальной точке решения F1s_, F2s.

Улучшения алгоритма для метода достижения цели

Метод достижения цели имеет то преимущество, что он может быть поставлен как проблема нелинейного программирования. Характеристики проблемы также могут быть использованы в алгоритме нелинейного программирования. В последовательном квадратичном программировании (SQP) выбор функции качества для поиска строки не является простым, поскольку во многих случаях трудно «определить» относительную важность между улучшением целевой функции и уменьшением нарушений ограничения. Это привело к ряду различных схем построения функции заслуг (см., например, Schittkowski [36]). В программировании достижения цели может быть более подходящая функция заслуг, которую вы можете достичь, представив уравнение 2 как задачу minimax

\underset{^{minimizex∈ℜn}}{} \underset{макси}{} {_{} Λ i

(3)

где

$_{Λ i} \frac{=_{} Fi (x_{)}^{}}{-_{}} Fi * wi, i =$ 1,..., m.

Следуя аргументу Brayton et al. [1] для оптимизации minimax с использованием SQP, использование функции качества уравнения 30 для задачи достижения цели уравнения 3 дает

(x, γ)_{}^{}_{}_{} =γ+\sumi=1mri\cdotmax{0,Fi (_{x}) -_{}^{} wiγ

− Fi *}.

(4)

Когда функция качества уравнения 4 используется в качестве основы для процедуры поиска строки, то, хотя (x, γ) может уменьшиться для шага в заданном направлении поиска, функцияmax _{Λ i} может парадоксальным образом увеличиться. Это означает признание деградации в худшем случае. Поскольку в худшем случае цель отвечает за значение целевой функции γ, это означает принятие шага, который в конечном итоге увеличивает целевую функцию, подлежащую минимизации. И наоборот, при max _{Λ i} уменьшается, подразумевая отказ от шага, который улучшает цель худшего случая.

Следуя строкам Brayton et al. [1], поэтому решение состоит в том, чтобы установить (x) равным цели наихудшего случая, т.е.

start(x) \underset{}{=}_{}

maxiΛ i.

(5)

Проблема в способе достижения цели заключается в том, что обычно для включения жестких ограничений используют весовой коэффициент, равный 0. Затем функция достоинств уравнения 5 становится бесконечной для произвольных нарушений ограничений.

Чтобы преодолеть эту проблему, сохраняя признаки уравнения 5, функцию качества объединяют с функцией уравнения 31, давая следующее:

(x)_{}^{} \begin{array}{l} _{}_{} =∑i=1m{ri⋅max{0,Fi (x_{)} -_{}^{} wiγ & −_{Fi} \\ \underset{если}{*},}_{} wi = 0maxiΛ i & , i = 1,. . \end{array}

., по-матерински.

(6)

Другой особенностью, которая может быть использована в SQP, является целевая функция γ. Из уравнений KKT можно показать, что приближение к гессену лагранжиана, H, должно иметь нули в строках и столбцах, связанных с переменной γ. Однако это свойство не появляется, если H инициализирован как единичная матрица. Поэтому H инициализируется и поддерживается, чтобы иметь нули в строках и столбцах, связанных с γ.

Эти изменения делают гессен, Н, бессрочным. Поэтому H устанавливается иметь нули в строках и столбцах, связанных с γ, за исключением диагонального элемента, который устанавливается в малое положительное число (например, 1e-10). Это позволяет использовать быстрый сходящийся положительный определенный метод QP, описанный в Quadratic Programming Solution.

Предыдущие модификации были реализованы в fgoalattain и были найдены, чтобы сделать способ более надежным. Однако из-за быстрой сходимости метода SQP требование, чтобы функция качества строго уменьшалась, иногда требует большего количества оценок функции, чем реализация SQP с использованием функции качества уравнения 30.

Минимизация максимальной цели

fminimax использует метод достижения цели. Требуется голы 0, а веса 1. С этой формулировкой проблема достижения цели становится

$\underset{}{} \underset{minimaxx}{} \frac{(_{} fi (x) -_{}}{_{}} \underset{}{goaliweighti)} \underset{}{=}_{}$ minimaxxfi (x),

что является проблемой minimax.

В скобках можно ожидать fminimax чтобы превратить многообъективную функцию в единую цель. Функция

f (x) = max ₍F1 (x),._.. Fj (x))

является единственной целевой функцией для минимизации. Однако это невозможно различить, и цели панели инструментов оптимизации должны быть плавными. Поэтому задача minimax формулируется как задача достижения гладкой цели.

Ссылки

[1] Брейтон, Р. К., С. В. Директор, Г. Д. Хахтель, и Л. Видигал, «Новый алгоритм для статистического проектирования цепей, основанный на квазиньютоновских методах и разделении функций», Транзакции IEEE на схемах и системах, том CAS-26, стр.

[2] Флеминг, П.Дж. и А.П. Пашкевич, Разработка автоматизированной системы управления с использованием подхода многоцелевой оптимизации, Конференция по контролю 1985, Кембридж, Великобритания, стр. 174-179.

[3] Гембицки, Ф. В., «Векторная оптимизация для управления с показателями производительности и чувствительности параметров», доктор философии. Диссертация, Case Western Reserve Univ., Кливленд, OH, 1974.

[4] Грейс, А.К.В., «Проектирование автоматизированной системы управления с использованием методов оптимизации», доктор философии. Дипломная работа, Уэльский университет, Бангор, Гвинед, Великобритания, 1989 год.

[5] Хан, С.П., «Глобально конвергентный метод нелинейного программирования», Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.

[6] Мадсен, К. и Х. Шьяер-Якобсен, «Алгоритмы оптимизации допусков в худшем случае», IEEE Trans. of Circuits and Systems, Vol. CAS-26, Sept. 1979.

[7] Пауэлл, M.J.D., «Быстрый алгоритм для вычислений нелинейной ограниченной оптимизации», Численный анализ, ред. Г.А. Уотсон, Лекционные заметки по математике, том 630, Springer Verlag, 1978.

Документация