Задание граничных нагрузок для несущей модели
structuralBoundaryLoad( определяет тягу поверхности, давление и поступательную жесткость на границе типа structuralmodel,RegionType,RegionID,'SurfaceTraction',STval,'Pressure',Pval,'TranslationalStiffness',TSval)RegionType с RegionID Идентификационные номера.
Тяга поверхности определяется как распределенные нормальные и тангенциальные силы, действующие на границе, разрешенной вдоль глобальной декартовой системы координат.
Давление должно быть указано в направлении, перпендикулярном границе. Положительное значение давления действует на границу (например, сжатие). Отрицательное давление действует в стороне от границы (например, всасывание).
Поступательная жесткость является распределенной пружинной жесткостью для каждого поступательного направления. Для моделирования упругого основания используют поступательную жесткость.
structuralBoundaryLoad не требует указания всех трех граничных нагрузок. В зависимости от проблемы структурного анализа можно указать одну или несколько граничных нагрузок, выбрав соответствующие аргументы и пропустив другие. Можно задать поступательную жесткость для любой несущей модели. Для определения давления или поверхностной тяги structuralmodel должна быть статической, переходной или частотной моделью отклика. Структурные модели для модального анализа не могут иметь давление или поверхностную тягу.
Граничная нагрузка по умолчанию является граничным условием без напряжения.
structuralBoundaryLoad( определяет сосредоточенную силу в вершине с помощью structuralmodel,'Vertex',VertexID,'Force',Fval)VertexID номер. Задать силу можно только в том случае, если structuralmodel - модель статической, переходной или частотной характеристики. Структурные модели для модального анализа не могут иметь концентрированную силу.
structuralBoundaryLoad(___,'Vectorized','on') использует вычисление векторизованной функции при передаче дескриптора функции в качестве аргумента. Если функция вычисляет векторизированным образом, то использование этого аргумента экономит время. См. раздел Векторизация. Дополнительные сведения об этой оценке см. в разделе Некондиционные граничные условия.
Используйте этот синтаксис с любым из входных аргументов из предыдущих синтаксисов.
structuralBoundaryLoad(___,'Pressure', позволяет задать форму и длительность нестационарного импульса давления и гармонического возбуждения для переходной структурной модели без создания дескриптора функции. При использовании этого синтаксиса необходимо указать модель, тип области, идентификатор области и давление. Тяга поверхности и поступательная жесткость являются необязательными аргументами. Этот синтаксис не работает для моделей статического, модального анализа и частотного отклика.Pval,Name,Value)
structuralBoundaryLoad( позволяет задать форму и длительность непостоянной концентрированной силы и гармонического возбуждения для переходной структурной модели без создания дескриптора функции.structuralmodel,'Vertex',VertexID,'Force',Fval,Name,Value)
boundaryLoad = structuralBoundaryLoad(___)
Наложите фиксированные границы и тягу на два конца биметаллического кабеля.
Создайте модель несущей конструкции.
structuralModel = createpde('structural','static-solid');
Создание вложенных цилиндров для моделирования биметаллического кабеля.
gm = multicylinder([0.01,0.015],0.05);
Назначьте геометрию несущей модели и постройте ее график.
structuralModel.Geometry = gm; pdegplot(structuralModel,'CellLabels','on','FaceLabels','on','FaceAlpha',0.4)
Для каждого металла укажите модуль Юнга и коэффициент Пуассона.
structuralProperties(structuralModel,'Cell',1,'YoungsModulus',110E9, ... 'PoissonsRatio',0.28); structuralProperties(structuralModel,'Cell',2,'YoungsModulus',210E9, ... 'PoissonsRatio',0.3);
Укажите, что грани 1 и 4 являются фиксированными границами.
structuralBC(structuralModel,'Face',[1,4],'Constraint','fixed')
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: [1 4]
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: "fixed"
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Задайте тягу поверхности для граней 2 и 5.
structuralBoundaryLoad(structuralModel,'Face',[2,5],'SurfaceTraction',[0;0;100])
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: [2 5]
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: [3x1 double]
Pressure: []
TranslationalStiffness: []
Создайте модель несущей конструкции.
structuralModel = createpde('structural','static-solid');
Создайте геометрию блока.
gm = multicuboid(20,10,5);
Назначьте геометрию несущей модели и постройте ее график.
structuralModel.Geometry = gm; pdegplot(structuralModel,'FaceLabels','on','FaceAlpha',0.5)
Укажите модуль Юнга и коэффициент Пуассона.
structuralProperties(structuralModel,'YoungsModulus',30, ... 'PoissonsRatio',0.3);
Нижняя поверхность блока опирается на упругий фундамент (пружину). Чтобы смоделировать этот фундамент, задайте поступательную жесткость.
structuralBoundaryLoad(structuralModel,'Face',1,'TranslationalStiffness',[0;0;30])
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 1
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: []
TranslationalStiffness: [3x1 double]
Задайте значение силы в вершине геометрии.
Создайте структурную модель для статического анализа твердотельной (3-D) задачи.
model = createpde('structural','static-solid');
Создайте геометрию, состоящую из двух кубов, расположенных друг над другом.
gm = multicuboid(0.2,0.01,[0.01 0.01],'Zoffset',[0 0.01]);Включите геометрию в модель несущей конструкции.
model.Geometry = gm;
Постройте график геометрии и отобразите метки граней. Поверните геометрию так, чтобы можно было видеть метки граней на левой стороне.
figure pdegplot(model,'FaceLabels','on'); view([-67 5])
Постройте график геометрии и отобразите метки вершин. Поверните геометрию так, чтобы можно было видеть метки вершин на правой стороне.
figure pdegplot(model,'VertexLabels','on','FaceAlpha',0.5) xlim([-0.01 0.1]) zlim([-0.01 0.02]) view([60 5])
Задайте модуль Юнга, коэффициент Пуассона и массовую плотность материала.
structuralProperties(model,'YoungsModulus',201E9,'PoissonsRatio',0.3);
Укажите, что грани 5 и 10 являются фиксированными границами.
structuralBC(model,'Face',[5 10],'Constraint','fixed');
Укажите сосредоточенную силу в вершине 6.
structuralBoundaryLoad(model,'Vertex',6,'Force',[0;10^4;0])
ans =
StructuralBC with properties:
RegionType: 'Vertex'
RegionID: 6
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: [3x1 double]
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Используйте дескриптор функции для задания частотно-зависимого давления для модели частотной характеристики.
Создайте модель частотной характеристики для 3-D проблемы.
fmodel = createpde('structural','frequency-solid');
Импорт и печать геометрии.
importGeometry(fmodel,'TuningFork.stl'); figure pdegplot(fmodel,'FaceLabels','on')
Укажите нагрузку давления на стойку (грань 11) в виде короткого прямоугольного импульса давления. В частотной области этот импульс давления представляет собой единичную нагрузку, равномерно распределенную по всем частотам.
structuralBoundaryLoad(fmodel,'Face',11,'Pressure',1);
Теперь задайте частотно-зависимую нагрузку давления, например, 2/100000.
pLoad = @(location,state) exp(-(state.frequency-1E3).^2/1E5); structuralBoundaryLoad(fmodel,'Face',12,'Pressure',pLoad);
Используйте дескриптор функции, чтобы задать гармонически изменяющееся давление в центре тонкой 3-D пластины.
Создайте переходную динамическую модель для 3-D проблемы.
structuralmodel = createpde('structural','transient-solid');
Создайте геометрию, состоящую из тонкой 3-D пластины с небольшой пластиной в центре. Включите геометрию в модель и выведите ее на печать.
gm = multicuboid([5,0.05],[5,0.05],0.01); structuralmodel.Geometry = gm; pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.5)
Увеличьте изображение, чтобы увидеть метки граней на маленькой пластине в центре.
figure pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.25) axis([-0.2 0.2 -0.2 0.2 -0.1 0.1])
Задайте модуль Юнга, коэффициент Пуассона и массовую плотность материала.
structuralProperties(structuralmodel,'YoungsModulus',210E9,... 'PoissonsRatio',0.3,... 'MassDensity',7800);
Укажите, что все грани на периферии тонкой 3-D пластины являются фиксированными границами.
structuralBC(structuralmodel,'Constraint','fixed','Face',5:8);
Приложите к небольшой грани в центре пластины нагрузку, изменяющуюся в гармоническом направлении.
plungerLoad = @(location,state)5E7.*sin(25.*state.time); structuralBoundaryLoad(structuralmodel,'Face',12,'Pressure',plungerLoad)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 12
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: @(location,state)5E7.*sin(25.*state.time)
TranslationalStiffness: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: []
EndTime: []
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Задайте гармонически изменяющееся давление в центре тонкой 3-D пластины, задав ее частоту.
Создайте переходную динамическую модель для 3-D проблемы.
structuralmodel = createpde('structural','transient-solid');
Создайте геометрию, состоящую из тонкой 3-D пластины с небольшой пластиной в центре. Включите геометрию в модель и выведите ее на печать.
gm = multicuboid([5,0.05],[5,0.05],0.01); structuralmodel.Geometry=gm; pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.5)
Увеличьте изображение, чтобы увидеть метки граней на маленькой пластине в центре.
figure pdegplot(structuralmodel,'FaceLabels','on','FaceAlpha',0.25) axis([-0.2 0.2 -0.2 0.2 -0.1 0.1])
Задайте модуль Юнга, коэффициент Пуассона и массовую плотность материала.
structuralProperties(structuralmodel,'YoungsModulus',210E9,... 'PoissonsRatio',0.3,... 'MassDensity',7800);
Укажите, что все грани на периферии тонкой 3-D пластины являются фиксированными границами.
structuralBC(structuralmodel,'Constraint','fixed','Face',5:8);
Приложите к небольшой грани в центре пластины нагрузку, изменяющуюся в гармоническом направлении.
structuralBoundaryLoad(structuralmodel,'Face',12,'Pressure',5E7,'Frequency',25)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 12
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: 50000000
TranslationalStiffness: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: []
EndTime: []
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: 25
Phase: []
Создайте переходную структурную модель.
structuralModel = createpde('structural','transient-solid');
Импорт и печать геометрии.
importGeometry(structuralModel,'BracketWithHole.stl'); pdegplot(structuralModel,'FaceLabels','on') view(-20,10)
Укажите модуль Юнга и коэффициент Пуассона.
structuralProperties(structuralModel,'YoungsModulus',200e9, ... 'PoissonsRatio',0.3,... 'MassDensity',7800);
Укажите, что грань 4 является фиксированной границей.
structuralBC(structuralModel,'Face',4,'Constraint','fixed');
Приложите прямоугольный импульс давления к грани 7 в направлении, перпендикулярном грани.
structuralBoundaryLoad(structuralModel,'Face',7,'Pressure',10^5,... 'StartTime',0.1,'EndTime',0.5)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 7
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: 100000
TranslationalStiffness: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: 0.1000
EndTime: 0.5000
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Задайте короткий импульс концентрированной силы в вершине геометрии.
Создайте структурную модель для статического анализа твердотельной (3-D) задачи.
structuralmodel = createpde('structural','transient-solid');
Создайте геометрию, состоящую из двух кубов, расположенных друг над другом.
gm = multicuboid(0.2,0.01,[0.01 0.01],'Zoffset',[0 0.01]);Включите геометрию в модель несущей конструкции.
structuralmodel.Geometry = gm;
Постройте график геометрии и отобразите метки граней. Поверните геометрию так, чтобы можно было видеть метки граней на левой стороне.
figure pdegplot(structuralmodel,'FaceLabels','on'); view([-67 5])
Постройте график геометрии и отобразите метки вершин. Поверните геометрию так, чтобы можно было видеть метки вершин на правой стороне.
figure pdegplot(structuralmodel,'VertexLabels','on','FaceAlpha',0.5) xlim([-0.01 0.1]) zlim([-0.01 0.02]) view([60 5])
Задайте модуль Юнга, коэффициент Пуассона и массовую плотность материала.
structuralProperties(structuralmodel,'YoungsModulus',201E9, ... 'PoissonsRatio',0.3, ... 'MassDensity',7800);
Укажите, что грани 5 и 10 являются фиксированными границами.
structuralBC(structuralmodel,'Face',[5 10],'Constraint','fixed');
Укажите короткий импульс концентрированной силы в вершине 6.
structuralBoundaryLoad(structuralmodel,'Vertex',6,'Force',[0;1000;0], ... 'StartTime',1,'EndTime',1.05)
ans =
StructuralBC with properties:
RegionType: 'Vertex'
RegionID: 6
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Boundary Loads
Force: [3×1 double]
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: 1
EndTime: 1.0500
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Задайте нулевое начальное смещение и скорость.
structuralIC(structuralmodel,'Displacement',[0;0;0],'Velocity',[0;0;0])
ans =
GeometricStructuralICs with properties:
RegionType: 'Cell'
RegionID: [1 2]
InitialDisplacement: [3×1 double]
InitialVelocity: [3×1 double]
Создайте тонкую сетку.
generateMesh(structuralmodel,'Hmax',0.02);Поскольку нагрузка равна нулю для начального интервала времени и применяется только в течение короткого времени, решите модель для двух интервалов времени. Используйте первый временной интервал, чтобы найти решение перед импульсом силы.
structuralresults1 = solve(structuralmodel,0:1E-2:1);
Используйте второй временной интервал, чтобы найти решение во время и после импульса силы.
structuralIC(structuralmodel,structuralresults1)
ans =
NodalStructuralICs with properties:
InitialDisplacement: [511×3 double]
InitialVelocity: [511×3 double]
structuralresults2 = solve(structuralmodel,[1.001:0.001:1.01 1.02:1E-2:2]);
Постройте график смещения в узле, соответствующем вершине 6, где применяется импульс концентрированной силы.
loadedNd = findNodes(structuralmodel.Mesh,'region','Vertex',6); plot(structuralresults2.SolutionTimes,structuralresults2.Displacement.uy(loadedNd,:))
structuralmodel - Структурная модельStructuralModel объектСтруктурная модель, заданная как StructuralModel объект. Модель содержит геометрию, сетку, структурные свойства материала, нагрузки на тело, граничные нагрузки и граничные условия.
Пример: structuralmodel = createpde('structural','transient-solid')
RegionType - Тип геометрической области'Edge' для модели 2-D | 'Face' для модели 3-DТип геометрической области, указанный как 'Edge' для модели 2-D или 'Face' для модели 3-D.
Пример: structuralBoundaryLoad(structuralmodel,'Face',[2,5],'SurfaceTraction',[0,0,100])
Типы данных: char | string
RegionID - Идентификатор геометрической областиИдентификатор геометрической области, заданный как положительное целое число или вектор положительных целых чисел. Поиск идентификаторов регионов с помощью pdegplot.
Пример: structuralBoundaryLoad(structuralmodel,'Face',[2,5],'SurfaceTraction',[0,0,100])
Типы данных: double
VertexID - Идентификатор вершиныИдентификатор вершины, заданный как положительное целое число или вектор положительных целых чисел. Поиск идентификаторов вершин с помощью pdegplot.
Пример: structuralBoundaryLoad(structuralmodel,'Vertex',6,'Force',[0;10^4;0])
Типы данных: double
STval - Распределенные нормальные и касательные силы на границеРаспределенные нормальные и касательные силы на границе, разрешенные вдоль глобальной декартовой системы координат, заданной как числовой вектор или дескриптор функции. Числовой вектор должен содержать два элемента для 2-D модели и три элемента для 3-D модели.
Функция должна возвращать двухстрочную матрицу для 2-D модели и трехстрочную матрицу для 3-D модели. Каждый столбец матрицы должен соответствовать вектору тяги поверхности в граничных координатах, предоставленных решателем. В случае анализа переходных или частотных характеристик, STval также может быть функцией времени или частоты соответственно. Дополнительные сведения см. в разделе Дополнительные сведения.
Пример: structuralBoundaryLoad(structuralmodel,'Face',[2,5],'SurfaceTraction',[0;0;100])
Типы данных: double | function_handle
Pval - Давление по нормали к границеДавление по нормали к границе, указанное как число или дескриптор функции. Давление положительного значения действует на границу (например, сжатие), в то время как давление отрицательного значения действует в стороне от границы (например, всасывание).
При указании Pval в качестве дескриптора функции функция должна возвращать вектор строки, где каждый столбец соответствует значению давления в граничных координатах, обеспечиваемых решателем. В случае переходной структурной модели, Pval также может быть функцией времени. В случае структурной модели частотной характеристики Pval может быть функцией частоты (если задана в качестве дескриптора функции) или постоянным давлением с одинаковой величиной для широкого частотного спектра. Дополнительные сведения см. в разделе Дополнительные сведения.
Пример: structuralBoundaryLoad(structuralmodel,'Face',[2,5],'Pressure',10^5)
Типы данных: double | function_handle
TSval - Распределенная жесткость пружиныРаспределенная жесткость пружины для каждого поступательного направления, используемого для моделирования упругого основания, заданного как числовой вектор или ручка функции. Числовой вектор должен содержать два элемента для 2-D модели и три элемента для 3-D модели. Пользовательская функция должна возвращать двухстрочную матрицу для 2-D модели и трехстрочную матрицу для 3-D модели. Каждый столбец этой матрицы соответствует вектору жесткости в граничных координатах, предоставленных решателем. В случае анализа переходных или частотных характеристик, TSval также может быть функцией времени или частоты соответственно. Дополнительные сведения см. в разделе Дополнительные сведения.
Пример: structuralBoundaryLoad(structuralmodel,'Edge',[2,5],'TranslationalStiffness',[0;5500])
Типы данных: double | function_handle
Fval - Концентрированная силаСосредоточенная сила в вершине, заданная как числовой вектор или дескриптор функции. Используйте дескриптор функции для указания концентрированной силы, зависящей от времени или частоты. Дополнительные сведения см. в разделе Дополнительные сведения.
Пример: structuralBoundaryLoad(structuralmodel,'Vertex',5,'Force',[0;0;10])
Типы данных: double | function_handle
structuralBoundaryLoad(structuralmodel,'Face',[2,5],'Pressure',10^5,'RiseTime',0.5,'FallTime',0.5,'EndTime',3)Используйте один или несколько аргументов пары имя-значение, чтобы указать форму и длительность импульса давления или концентрированной силы и гармонического возбуждения только для переходной структурной модели. Задайте значение давления или силы с помощью Pval или Fval аргумент, соответственно.
Можно моделировать прямоугольные, треугольные и трапециевидные импульсы давления или концентрированной силы. Если время начала равно 0, его можно не указывать.
Для прямоугольного импульса укажите время начала и окончания.
Для треугольного импульса укажите время начала и любое из двух следующих значений: время нарастания, время падения и время окончания. Можно также указать все три раза, но они должны быть непротиворечивыми.
Для трапециевидного импульса укажите все четыре раза.
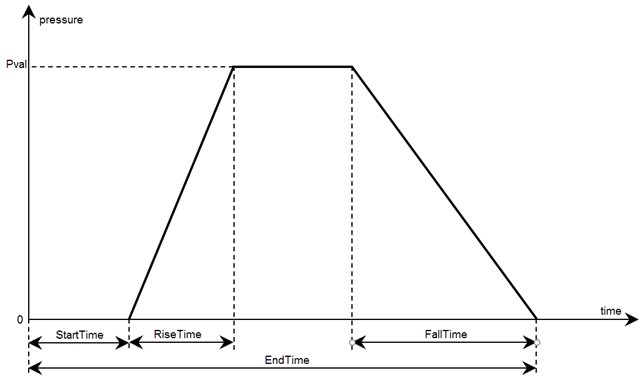
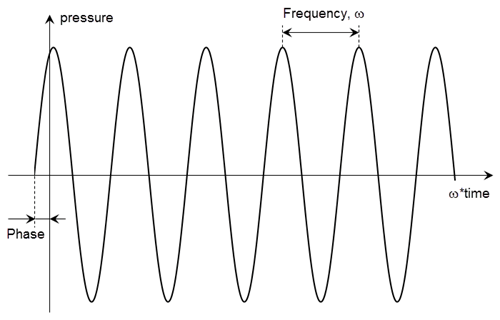
Можно моделировать гармоническое давление или нагрузку концентрированной силы, задав ее частоту и начальную фазу. Если начальная фаза равна 0, ее можно не указывать.
structuralBC | Свойства Structural BC | structuralBodyLoad | structuralDamping | StructuralModel | structuralProperties