Дискретный наблюдатель Люенбергера
Simscape / Электрический / Контроль / Наблюдатели

Блок Luenberger Observer реализует дискретное время Luenberger observer. Этот блок используется для оценки состояний наблюдаемой системы с помощью:
Дискретные входы и выходы системы.
Дискретное представление состояния и пространства системы.
Luenberger Observer также иногда называют государственным наблюдателем или просто наблюдателем.
Вы можете управлять системами с множеством входов и множеством выходов, передавая вектор выходного состояния этого блока в блок контроллера обратной связи состояния.
Блок реализует дискретное время Luenberger Observer с помощью обратного метода Эйлера благодаря своей простоте и стабильности.
Оценщик задается этим уравнением разности:
k) − y ^ (k)),
где:
k) - k-ый оцененный вектор состояния.
k) - k-ый оцененный выходной вектор.
u (k) - k-й входной вектор.
y (k) - k-ый измеренный выходной вектор.
Ad - это дискретизированная матрица состояния.
Bd - дискретизированная входная матрица.
Ld - дискретизированная матрица усиления наблюдателя.
Динамика ошибки оценки описывается:
LdCd) e (k),
где:
e (k) - k-й вектор ошибок.
Cd является выходной матрицей.
Ошибка оценки сходится к нулю, когда Ad-LdCD имеет собственные значения внутри единичной окружности. Поэтому значение Ld должно быть таким, чтобы эта цель была достигнута. Блок вычисляет коэффициент усиления наблюдателя путем решения
− 1,
где G - произвольная матрица и X получается решением уравнения Сильвестра:
CdTG.
Здесь Λ является матрицей с требуемыми собственными значениями, которые не совпадают с собственными значениями Ad. На этой диаграмме показана основная структура дискретного времени Luenberger Observer.
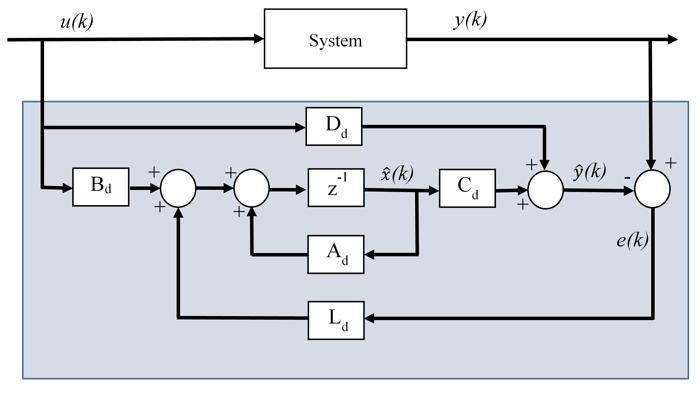
Система является наблюдаемой, что справедливо, если состояние системы может быть определено по входу и выходу за конечное время. Математически это означает, что матрица наблюдаемости системы имеет полный ранг.
Требуемые собственные значения не совпадают с собственными значениями модели с разомкнутым контуром.
[1] Люенбергер, Д. Г. «Введение в наблюдателей». Транзакции IEEE при автоматическом управлении. Том 16, номер 6, 1971, стр. 596-602.
[2] Алессандри, А. и П. Колетта. «Дизайн Luenberger наблюдателей для класса гибридных линейных систем». В Международном рабочем совещании по гибридным системам: вычисления и управление, Берлин, март 2001 года.
[3] Варга, А. «Надежное назначение полюсов посредством параметризации обратной связи состояния на основе уравнения Сильвестра». В «Computer-Aided Control System Design», стр. 13-18., Анкоридж, Аляска, 2000.