Воздушный зазор между зубцом статора и вращающимся ротором постоянного магнита
Simscape / Электрический / Электромеханический
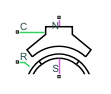
Блок «Вращающийся воздушный зазор» моделирует воздушный зазор между зубцом статора и вращающимся ротором постоянного магнита. Этот блок предполагает, что магниты ротора установлены на поверхности и что соответствующее индуцированное напряжение является синусоидальным.
Если угол ротора равен нулю, определяемый переменной угла ротора на вкладке Переменные (Variables), то магнит ротора идеально совмещается с серединой первого зубца статора. Затем постоянный магнит ориентируют таким образом, чтобы он противостоял потоку потока от порта N к порту S.
Этот блок используется для создания магнитного представления синхронного двигателя с постоянным магнитом (PMSM). Например, если требуется смоделировать двигатель с девятью полюсами статора, создайте девять копий этого блока и задайте для каждого из параметров индекса привязки зуба статора значение 1, 2, 3, 4, 5, 6, 7, 8, и 9соответственно.
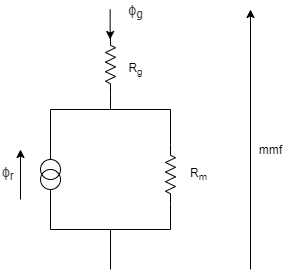
На этом рисунке показана эквивалентная цепь для воздушного зазора и соседнего постоянного магнита.
где:
β g - магнитный поток, который протекает от внешнего магнитного контура к порту N.
Rg - сопротивление воздушного зазора.
mmf - магнитодвигательная сила на вращающемся компоненте воздушного зазора.
Rm - сопротивление постоянного магнита.
β r - магнитный поток, генерируемый постоянными магнитами ротора в угловом диапазоне, охватываемом зубцом статора.
Это уравнение определяет соотношение между (g), (m) f и (r) r:
Если обратная ЭДС является синусоидальной, плотность потока ротора постоянного магнита определяется этим уравнением.
где:
N - число пар полюсов ротора.
startr - угол поворота ротора.
δs - угол статора.
B0 - плотность магнитного потока Пика, в Tesla.
Затем, чтобы получить связь постоянного магнитного потока, интегрируйте по углу статора, стягиваемому зубцом статора.
[B0cos (Nθs−Nθr)] dθs
где:
r - радиус ротора.
l - глубина зуба (в направлении вала).
Для идеальной PMSM, величина, которая должна быть равна 2π/Ns, где Ns - значение параметра Число зубьев статора. Тогда уравнение потока, который протекает по эквивалентной схеме, получается решением интеграла:
(Nα r).
Чтобы получить крутящий момент, создаваемый через воздушный зазор, сначала вычислите общую энергию, накопленную компонентом:
2Rm.
Затем для получения крутящего момента дифференцируйте относительно угла ротора:
(θr))/N.
Наконец, вычислите Rg и Rm с точки зрения геометрии:
lmμrμ0Ag
где:
мк0 - диэлектрическая проницаемость свободного пространства.
мкr - относительная диэлектрическая проницаемость постоянного магнита.
g - воздушный зазор.
lm - длина магнита.
Раздел «Переменные» интерфейса блока используется для установки приоритетов и начальных целевых значений для переменных блока перед моделированием. Дополнительные сведения см. в разделе Установка приоритета и начальной цели для переменных блока.