Синтез контроллеров H∞ с планированием усиления
[gopt,pdK,R,S] = hinfgs(pdP,r,gmin,tol,tolred)
Дано аффинное зависимое от параметров растение
D12uy = C2x + D21w + D22u
где изменяющийся во времени вектор параметров p (t) находится в диапазоне в рамке и измеряется в реальном времени ,hinfgs ищет аффинный контроллер, зависящий от параметров
DK (P) y
запланированные измерениями p (t) и такие, что
K стабилизирует замкнутую систему
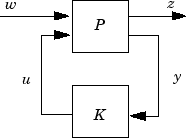
для всех допустимых траекторий параметров p (t)
K минимизирует производительность квадратичного H∞ с замкнутым контуром от w до z.
Описание pdP зависящей от параметра установки P указывается psys и вектор r дает количество входов и выходов контроллера (набор r=[p2,m2] если y ∊ Rp2 и u ∊ Rm2). Обратите внимание, что hinfgs также принимает политопическую модель возвращаемого P, например, aff2pol.
hinfgs возвращает оптимальную квадратичную производительность с замкнутым контуром gopt и политопическое описание контроллера, запланированного для усиления pdK. Чтобы проверить достижимость квадратичной характеристики γ замкнутого контура, установите третий вход gmin к γ. Аргументы tol и tolred контролировать требуемую относительную точность на gopt и пороговое значение для сокращения заказов. Наконец, hinfgs также возвращает решения R, S характерной системы LMI.
Контроллер по расписанию усиления pdK параметризуется p (t) и характеризуется значениями KΔj DK (p)) в углах ³ j блока параметров. Команда
Kj = psinfo(pdK,'sys',j)
возвращает j-й контроллер вершин KSecurityj, пока
pv = psinfo(pdP,'par') vertx = polydec(pv) Pj = vertx(:,j)
дает соответствующий угол ³ j поля параметров (pv - описание вектора параметра).
Планирование контроллера должно выполняться следующим образом. Учитывая измерения p (t) параметров в момент времени t,
Экспресс p (t) в виде выпуклой комбинации ³ j:
αj≥0,∑i=1Nαj=1
Это выпуклое разложение вычисляется с помощью polydec.
Вычислите матрицы состояния-пространства контроллера в момент времени t как выпуклую комбинацию контроллеров вершин KSecurityj:
=∑i=1NαjKΠι.
Используйте AK (t), BK (t), CK (t), DK (t) для обновления уравнений состояния-пространства контроллера.
Apkarian, P., P. Gahinet и G. Becker, «Саморегулируемое H∞ управление линейными изменяющимися параметрами системами», Automatica, 31 (1995), pp. 1251-1261.
Becker, G., Packard, P., «Надежная производительность линейно-параметрически изменяющихся систем с использованием параметрически зависимой линейной обратной связи», Systems and Control Letters, 23 (1994), pp. 205-215.
Packard, A., «Планирование усиления посредством линейных дробных преобразований», System. Contr. Письма, 22 (1994), стр. 79-92.