Методы параметрического моделирования находят параметры для математической модели, описывающей сигнал, систему или процесс. Эти методы используют известную информацию о системе для определения модели. Приложения для параметрического моделирования включают синтез речи и музыки, сжатие данных, спектральную оценку высокого разрешения, связь, производство и моделирование.
Функции параметрического моделирования панели инструментов работают с моделью рациональной передаточной функции. Учитывая соответствующую информацию о неизвестной системе (данные импульсной или частотной характеристики, или входные и выходные последовательности), эти функции находят коэффициенты линейной системы, которая моделирует систему.
Одним из важных применений функций параметрического моделирования является разработка фильтров с заданной временной или частотной характеристикой.
Ниже приведена сводка функций параметрического моделирования на этой панели инструментов.
Область | Функции | Описание |
|---|---|---|
Время | Создайте коэффициенты всеполюсного фильтра, которые моделируют последовательность входных данных с помощью алгоритма Левинсона-Дурбина. | |
Создайте коэффициенты полюсного фильтра, которые моделируют последовательность входных данных путем минимизации ошибки прямого предсказания. | ||
Создайте коэффициенты полюсного фильтра, которые моделируют последовательность входных данных, минимизируя ошибки прямого и обратного прогнозирования. | ||
Создайте коэффициенты всеполюсного фильтра, которые моделируют последовательность входных данных, используя оценку автокорреляционной функции. | ||
Линейное предиктивное кодирование. Создайте всеполюсный рекурсивный фильтр, импульсная характеристика которого соответствует заданной последовательности. | ||
Создайте фильтр БИХ, импульсная характеристика которого соответствует заданной последовательности. | ||
Найдите фильтр IIR, выходные данные которого, заданная последовательность ввода, соответствует заданной последовательности вывода. | ||
Частота | Генерируют коэффициенты цифрового или аналогового фильтра, полученные из данных комплексного частотного отклика. |
lpc, prony, и stmcb функции находят коэффициенты цифровой рациональной передаточной функции, которая аппроксимирует данную импульсную характеристику временной области. Алгоритмы отличаются сложностью и точностью получаемой модели.
Моделирование линейного прогнозирования предполагает, что каждая выходная выборка сигнала, x(k), является линейной комбинацией прошлого n выходные сигналы (то есть они могут быть линейно предсказаны из этих выходных сигналов), и что коэффициенты являются постоянными от выборки к выборке:
−⋯−a (n + 1) x (k − n).
Один nвсеполюсная модель сигнала th-го порядка x является
a = lpc(x,n)
Проиллюстрировать lpc, создать сигнал выборки, который является импульсной характеристикой всеполюсного фильтра с аддитивным белым шумом:
x = impz(1,[1 0.1 0.1 0.1 0.1],10) + randn(10,1)/10;
Коэффициенты для полнополюсного фильтра четвертого порядка, моделирующего систему:
a = lpc(x,4)
lpc первые вызовы xcorr найти смещенную оценку корреляционной функции x, а затем использует рекурсию Левинсона-Дурбина, реализованную в levinson функция, чтобы найти коэффициенты модели a. Рекурсия Левинсона - Дурбина - быстрый алгоритм решения системы симметричных линейных уравнений Теплица. lpcвесь алгоритм для n = 4 является
r = xcorr(x);
r(1:length(x)-1) = []; % Remove corr. at negative lags
a = levinson(r,4)
Вы можете сформировать коэффициенты линейного прогнозирования с другими допущениями, передав другую оценку корреляции levinson, такие как смещенная оценка корреляции:
r = xcorr(x,'biased'); r(1:length(x)-1) = []; % Remove corr. at negative lags a = levinson(r,4)
prony функция моделирует сигнал, используя заданное число полюсов и нулей. Задана последовательность x и порядки числителей и знаменателей n и m, соответственно, утверждение
[b,a] = prony(x,n,m)
находит числитель и коэффициенты знаменателя БИХ-фильтра, импульсная характеристика которого аппроксимирует последовательность x.
prony функция реализует метод, описанный в [4] Parks and Burrus. Этот метод использует вариацию ковариационного метода AR моделирования, чтобы найти коэффициенты знаменателя a, а затем находит числительные коэффициенты b для которого импульсная характеристика результирующего фильтра точно соответствует первой n + 1 образцы x. Фильтр не обязательно стабилен, но потенциально он может восстановить коэффициенты точно, если последовательность данных действительно является процессом авторегрессионного скользящего среднего (ARMA) правильного порядка.
Примечание
Функции prony и stmcb (описаны далее) более точно описаны как модели ARX в терминологии идентификации системы. Моделирование ARMA предполагает шум только на входах, в то время как ARX предполагает внешний вход. prony и stmcb знать входной сигнал: это импульс для prony и является произвольным для stmcb.
Модель для тестовой последовательности x (из более ранних lpc пример) с использованием фильтра IIR третьего порядка
[b,a] = prony(x,3,3)
impz показывает, насколько хорошо импульсная характеристика этого фильтра соответствует исходной последовательности:
format long
[x impz(b,a,10)]
Обратите внимание, что первые четыре образца точно совпадают. Для примера точного восстановления восстановите коэффициенты фильтра Баттерворта из его импульсной характеристики:
[b,a] = butter(4,.2); h = impz(b,a,26); [bb,aa] = prony(h,4,4);
Попробуйте этот пример; вы увидите, что bb и aa соответствует исходным коэффициентам фильтра в пределах допуска 10-13.
stmcb функция определяет коэффициенты для системы b (z )/a (z) с приблизительной импульсной характеристикойx, а также желаемое количество нулей и полюсов. Эта функция идентифицирует неизвестную систему на основе как входных, так и выходных последовательностей, которые описывают поведение системы или только импульсную характеристику системы. В режиме по умолчанию stmcb работает, как prony.
[b,a] = stmcb(x,3,3)
stmcb также находит системы, которые соответствуют заданным входным и выходным последовательностям:
y = filter(1,[1 1],x); % Create an output signal.
[b,a] = stmcb(y,x,0,1)
В этом примере: stmcb правильно определяет систему, используемую для создания y от x.
Метод Стейглица - Макбрайда - быстрый итеративный алгоритм, который решает для числителя и знаменателя коэффициенты одновременно в попытке минимизировать ошибку сигнала между выходом фильтра и заданным выходным сигналом. Этот алгоритм обычно быстро сходится, но может и не сходиться, если порядок модели слишком велик. Что касается prony, stmcbРезультирующий фильтр не обязательно стабилен из-за его точного подхода к моделированию.
stmcb обеспечивает контроль нескольких важных алгоритмических параметров; при возникновении проблем с моделированием данных измените эти параметры. Чтобы изменить число итераций из значения по умолчанию, равного пяти, и предоставить начальную оценку для коэффициентов знаменателя:
n = 10; % Number of iterations a = lpc(x,3); % Initial estimates for denominator [b,a] = stmcb(x,3,3,n,a);
Функция использует модель из всех полюсов, созданную с помощью prony в качестве первоначальной оценки, когда вы не предоставляете свою собственную оценку.
Сравнение функций lpc, prony, и stmcb, вычислить ошибку сигнала в каждом случае:
a1 = lpc(x,3); [b2,a2] = prony(x,3,3); [b3,a3] = stmcb(x,3,3); [x-impz(1,a1,10) x-impz(b2,a2,10) x-impz(b3,a3,10)]
При сравнении возможностей моделирования для модели IIR заданного порядка последний результат показывает, что для этого примера: stmcb работает лучше всех, а затем prony, то lpc. Эта относительная производительность типична для функций моделирования.
invfreqs и invfreqz функции реализуют обратные операции freqs и freqz; они находят аналоговую или цифровую передаточную функцию заданного порядка, которая соответствует заданной комплексной частотной характеристике. Хотя следующие примеры демонстрируют invfreqz, обсуждение также относится к invfreqs.
Для восстановления исходных коэффициентов фильтра из частотной характеристики простого цифрового фильтра:
[b,a] = butter(4,0.4) % Design Butterworth lowpass [h,w] = freqz(b,a,64); % Compute frequency response [b4,a4] = invfreqz(h,w,4,4) % Model: n = 4, m = 4
Вектор частот w имеет единицы в рад/выборке, и частоты не обязательно должны быть равномерно разнесены. invfreqz находит фильтр любого порядка для соответствия частотным данным; пример третьего порядка:
[b4,a4] = invfreqz(h,w,3,3) % Find third-order IIR
Оба invfreqs и invfreqz расчетные фильтры с реальными коэффициентами; для точки данных с положительной частотой f, функции соответствуют частотной характеристике в обоих f и -f.
По умолчанию invfreqz использует метод ошибки уравнения для определения наилучшей модели из данных. Это находит b и a в
![]()
путем создания системы линейных уравнений и их решения с помощью MATLAB
®\ оператор. Здесь A (w (k)) и B (w (k)) являются преобразованиями Фурье многочленовa и b соответственно на частоте w (k), а n - количество частотных точек (длина h и w). wt (k) весит ошибку относительно ошибки на различных частотах. Синтаксис
invfreqz(h,w,n,m,wt)
включает в себя весовой вектор. В этом режиме фильтр в результате invfreqz гарантированно не будет стабильным.
invfreqz обеспечивает превосходный алгоритм («вывод-ошибка»), который решает прямую задачу минимизации взвешенной суммы квадратичной ошибки между фактическими точками частотной характеристики и желаемым откликом
![]()
Чтобы использовать этот алгоритм, укажите параметр для подсчета итераций после параметра весового вектора:
wt = ones(size(w)); % Create unit weighting vector [b30,a30] = invfreqz(h,w,3,3,wt,30) % 30 iterations
Полученный фильтр всегда стабилен.
Графически сравните результаты первого и второго алгоритмов с исходным фильтром Баттерворта с FVTool (и выберите величины и фазовые отклики):
fvtool(b,a,b4,a4,b30,a30)
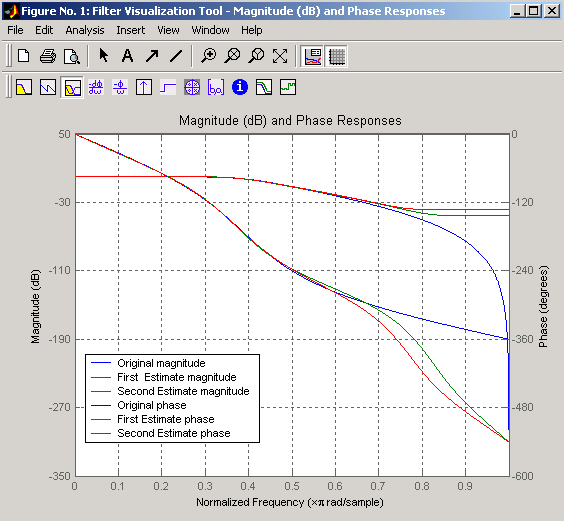
Чтобы проверить превосходство посадки численно, введите
sum(abs(h-freqz(b4,a4,w)).^2) % Total error, algorithm 1 sum(abs(h-freqz(b30,a30,w)).^2) % Total error, algorithm 2