Для решения математических задач с помощью символьных математических Toolbox™ определите символические объекты для представления различных математических объектов. В этом примере рассматривается использование следующих символических объектов:
символические числа
символьные скалярные переменные, функции и выражения
символические уравнения
символьные векторы и матрицы
символьные переменные матрицы (с R2021a года)
Определение числа как символического числа предписывает MATLAB ® рассматривать число как точную форму вместо использования числового приближения. Например, используйте символическое число, чтобы представить аргумент обратной тригонометрической функции, ().

Создайте символическое число с помощью symи назначить его a.
a = sym(1/sqrt(2))
a = 2^(1/2)/2
Найти обратный синус a. Результатом является символическое число pi/4.
thetaSym = asin(a)
thetaSym = pi/4
Можно преобразовать символьное число в арифметику переменной точности с помощью vpa. Результатом является десятичное число с 32 значимыми цифрами.
thetaVpa = vpa(thetaSym)
thetaVpa = 0.78539816339744830961566084581988
Чтобы преобразовать символьное число в число с двойной точностью, используйте double. Дополнительные сведения об использовании числовой или символьной арифметики см. в разделе Выбор числовой или символьной арифметики.
thetaDouble = double(thetaSym)
thetaDouble = 0.7854
Определение переменных, функций и выражений в качестве символических объектов позволяет выполнять алгебраические операции с этими символическими объектами, включая упрощение формул и решение уравнений. Например, используйте символическую скалярную переменную, функцию и выражение для представления квадратичной функции + x − 2. Для краткости символическая скалярная переменная также называется символической переменной.

Создание символьной скалярной переменной x использование syms. Также можно использовать sym для создания символьной скалярной переменной. Дополнительные сведения об использовании syms или symсм. раздел Выбор функции syms или sym. Определение символического выражения x^2 + x - 2 для представления правой части квадратичного уравнения и назначения его f(x). Идентификатор f(x) теперь относится к символьной функции, которая представляет квадратичную функцию.
syms x f(x) = x^2 + x - 2
f(x) = x^2 + x -2
Затем можно вычислить квадратичную функцию, указав ее входной аргумент в скобках. Например, вычислить f(2).
fVal = f(2)
fVal = 4
Можно также решить квадратичное уравнение = 0. Использоватьsolve чтобы найти корни квадратичного уравнения. solve возвращает два решения в виде вектора из двух символьных чисел.
sols = solve(f)
sols = -2 1
Определение математического уравнения как символического уравнения позволяет найти решение уравнения. Например, используйте символическое уравнение для решения тригонометрической задачи ) = 1.
![]()
Создание символической функции g(t) использование syms. Назначение символьного выражения 2*sin(t)*cos(t) кому g(t).
syms g(t) g(t) = 2*sin(t)*cos(t)
g(t) = 2*cos(t)*sin(t)
== оператор и назначение математического отношения g(t) == 1 кому eqn. Идентификатор eqn - символическое уравнение, представляющее тригонометрическую задачу.eqn = g(t) == 1
eqn = 2*cos(t)*sin(t) == 1
Использовать solve найти решение тригонометрической задачи.
sol = solve(eqn)
sol = pi/4
Используйте символьный вектор и матрицу для представления и решения системы линейных уравнений.
+ 5y = v
Систему уравнений можно представить в виде вектора двух символьных уравнений. Можно также представить систему уравнений как задачу матрицы, включающую матрицу символьных чисел и вектор символьных переменных. Для краткости любой вектор символических объектов называется символическим вектором, а любая матрица символических объектов - символической матрицей.
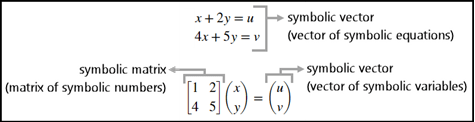
Создание двух символьных уравнений eq1 и eq2. Объединение двух уравнений в символьный вектор.
syms u v x y eq1 = x + 2*y == u; eq2 = 4*x + 5*y == v; eqns = [eq1, eq2]
eqns = [x + 2*y == u, 4*x + 5*y == v]
Использовать solve найти решения системы уравнений, представленных eqns. solve возвращает структуру S с полями, названными по каждой из переменных в уравнениях. Доступ к решениям можно получить с помощью точечной нотации, как S.x и S.y.
S = solve(eqns); S.x
ans = (2*v)/3 - (5*u)/3
S.y
ans = (4*u)/3 - v/3
Другим способом решения системы линейных уравнений является преобразование её в матричную форму. Использовать equationsToMatrix для преобразования системы уравнений в матричную форму и назначения вывода A и b. Здесь, A является символьной матрицей и b является символическим вектором. Решите проблему матрицы с помощью оператора matrix division\.
[A,b] = equationsToMatrix(eqns,x,y)
A = [1, 2] [4, 5] b = u v
sols = A\b
sols =
(2*v)/3 - (5*u)/3
(4*u)/3 - v/3С R2021a г.
Используйте переменные символьной матрицы для вычисления разностей относительно векторов.
Переменные символьной матрицы представляют матрицы, векторы и скаляры как атомарные символы. Символьные матричные переменные обеспечивают лаконичное отображение в наборном наборе и показывают математические формулы с большей четкостью. Можно брать векторные выражения из учебников и вводить их в инструментарий символьной математики.

Создание трех символьных переменных матрицы x, y, и A с использованием syms с помощью команды matrix аргумент. Нескалярные символьные переменные матрицы отображаются полужирным шрифтом в окне команд и в интерактивном редакторе.
syms x [4 1] matrix syms y [3 1] matrix syms A [3 4] matrix x y A
x = x y = y A = A
alpha. Найти дифференциал alpha относительно векторов x и y, которые представлены символьными матричными переменными x и y.alpha = y.'*A*x
alpha = y.'*A*x
diff(alpha,x)
ans = y.'*A
diff(alpha,y)
alpha = x.'*A.'
В этой таблице сравниваются различные символьные объекты, доступные в инструменте «Символьная математика» (Symbolic Math Toolbox).
| Символические объекты | Примеры команд MATLAB | Размер символических объектов | Тип данных |
|---|---|---|---|
| символическое число |
a = 1/sqrt(sym(2)) theta = asin(a) a = 2^(1/2)/2 theta = pi/4 | 1около-1 | sym |
| символьная скалярная переменная |
syms x y u v | 1около-1 | sym |
| символическая функция |
syms x f(x) = x^2 + x - 2 syms g(t) g(t) = 2*sin(t)*cos(t) f(x) = x^2 + x - 2 g(t) = 2*cos(t)*sin(t) | 1около-1 | symfun |
| символическое уравнение |
syms u v x y eq1 = x + 2*y == u eq2 = 4*x + 5*y == v eq1 = x + 2*y == u eq2 = 4*x + 5*y == v | 1около-1 | sym |
| символическое выражение |
syms x expr = x^2 + x - 2 expr2 = 2*sin(x)*cos(x) expr = x^2 + x - 2 expr2 = 2*cos(x)*sin(x) | 1около-1 | sym |
| символический вектор |
syms u v b = [u v] b = [u, v] | 1около-n или mоколо-1 | sym |
| символьная матрица |
syms A x y A = [x y; x*y y^2] A = [ x, y] [x*y, y^2] | mоколо-n | sym |
| символьный многомерный массив |
syms A [2 1 2] A A(:,:,1) = A1_1 A2_1 A(:,:,2) = A1_2 A2_2 | sz1около-sz2-...-szn | sym |
| символьная переменная матрицы (с R2021a года) |
syms A B [2 3] matrix A B A B | mоколо-n | symmatrix |
str2sym | sym | symfun | symmatrix | symmatrix2sym | syms