orthfilt

Набор ортогональных вейвлет-фильтров

Синтаксис

[Lo_D,Hi_D,Lo_R,Hi_R] = orthfilt(W)

Описание

[Lo_D,Hi_D,Lo_R,Hi_R] = orthfilt(W) вычисляет четыре фильтра, связанные с фильтром масштабирования W соответствующий вейвлету:

`Lo_D`	Разложение фильтра нижних частот
`Hi_D`	Фильтр высокой частоты разложения
`Lo_R`	Реконструкция фильтра нижних частот
`Hi_R`	Реконструкция фильтра верхних частот

Для ортогонального вейвлета в фреймворке множественного разрешения мы начинаем с масштабной функции, а затем с вейвлет-функции. Одним из фундаментальных отношений является двухмасштабное отношение:

$\frac{}{} 12start(\frac{}{} x2) \underset{}{}_{} =∑n∈Zwnϕ (x$ − n)

Все фильтры, используемые в dwt и idwt тесно связаны с последовательностью ${(_{wn})}_{}$ n∈Z. Совершенно очевидно, что, если startкомпактно поддерживается, последовательность (_wn) является конечной и может рассматриваться как фильтр FIR. Фильтр масштабированияW является

Фильтр ПИХ нижних частот
Длины 2N
Суммы 1
Нормы

Например, для db3 фильтр масштабирования,

load db3 
db3
db3 =
    0.2352 0.5706 0.3252 -0.0955 -0.0604 0.0249

sum(db3)
ans =
    1.000
    norm(db3)
ans =
    0.7071

Из фильтра W, мы определяем четыре фильтра FIR длиной 2N и нормой 1, организованных следующим образом:

Фильтры	Низкопроходная	Высокопроходимая
Разложение	`Lo_D`	`Hi_D`
Реконструкция	`Lo_R`	`Hi_R`

Четыре фильтра вычисляются по следующей схеме:

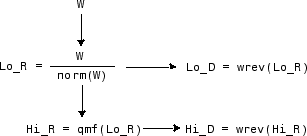
где qmf таков, что Hi_R и Lo_R - квадратурные зеркальные фильтры (т. е. Hi_R(k) = (-1)^kLo_R(2N + 1 - k), для k = 1, 2, Ä, 2N) и где wrev разворачивает коэффициенты фильтра. Так Hi_D и Lo_D также являются квадратурными зеркальными фильтрами. Вычисление этих фильтров выполняется с помощью orthfilt.

Примеры

% Load scaling filter. 
load db8; w = db8; 
subplot(421); stem(w); 
title('Original scaling filter');

% Compute the four filters. 
[Lo_D,Hi_D,Lo_R,Hi_R] = orthfilt(w); 
subplot(423); stem(Lo_D); 
title('Decomposition low-pass filter'); 
subplot(424); stem(Hi_D); 
title('Decomposition high-pass filter'); 
subplot(425); stem(Lo_R); 
title('Reconstruction low-pass filter'); 
subplot(426); stem(Hi_R); 
title('Reconstruction high-pass filter');

% Check for orthonormality. 
df = [Lo_D;Hi_D];
rf = [Lo_R;Hi_R];
id = df*df'

id =
    1.0000         0
         0    1.0000

id = rf*rf'

id =
    1.0000         0
         0    1.0000

% Check for orthogonality by dyadic translation, for example:
df = [Lo_D 0 0;Hi_D 0 0]; 
dft = [0 0 Lo_D; 0 0 Hi_D]; 
zer = df*dft'

zer =

    1.0e-12 *
    -0.1883 0.0000
    -0.0000 -0.1883

% High- and low-frequency illustration. 
fftld = fft(Lo_D); ffthd = fft(Hi_D); 
freq = [1:length(Lo_D)]/length(Lo_D); 
subplot(427); plot(freq,abs(fftld)); 
title('Transfer modulus: low-pass');
subplot(428); plot(freq,abs(ffthd)); 
title('Transfer modulus: high-pass')
% Editing some graphical properties,
% the following figure is generated.

Ссылки

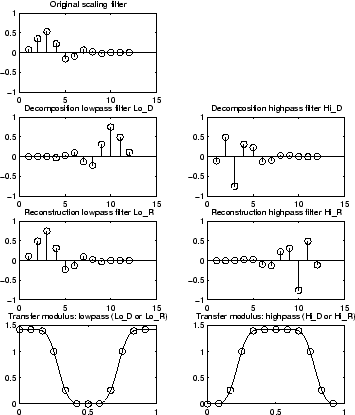
Daubechies, I. (1992), Десять лекций по вейвлетам, CBMS-NSF серии конференций по прикладной математике, SIAM Ed. стр. 117-119, 137, 152.

См. также

biorfilt | qmf | wfilters

Представлен до R2006a

Документация