Дискретное стационарное вейвлет-преобразование 1-D
Выполните многоуровневое стационарное вейвлет-разложение сигнала.
Загрузите одномерный сигнал и получите его длину.
load noisbloc
s = noisbloc;
sLen = length(s);Выполнить стационарную вейвлет-декомпозицию на уровне 3 сигнала с использованием 'db1'. Извлеките коэффициенты детализации и аппроксимации на уровне 3.
[swa,swd] = swt(s,3,'db1');
swd3 = swd(3,:);
swa3 = swa(3,:);Постройте график выходных данных разложения.
plot(s)
xlim([0 sLen])
title('Original Signal')
Постройте график коэффициентов приближения и детализации уровня 3.
subplot(2,1,1) plot(swa3) xlim([0 sLen]) title('Level 3 Approximation coefficients') subplot(2,1,2) plot(swd3) xlim([0 sLen]) title('Level 3 Detail coefficients')
Учитывая сигнал s длиной N, первый этап стационарного вейвлет-преобразования (SWT) производит, начиная с s, два набора коэффициентов: коэффициенты аппроксимации cA1 и коэффициенты детализации cD1. Эти векторы получаются сверткой s с фильтром нижних частот LoD для аппроксимации и с фильтром верхних частот HiD для получения подробной информации.
Точнее, первый шаг -
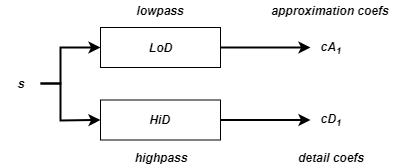
где
обозначает свертку с фильтром X.
Примечание
cA1 и cD1 имеют длину N вместо N/2 как в случае DWT.
На следующем этапе коэффициенты аппроксимации разбиваются cA1 на две части, используя одну и ту же схему, но с модифицированными фильтрами, полученными путем повышения дискретизации фильтров, использованных на предыдущем этапе, и замены s на cA1. Затем SWT производит cA2 и cD2. В более общем плане
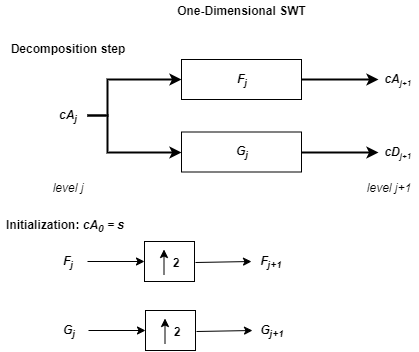
где
F0 = LoD
G0 = HiD
- Upsample (вставка нулей между элементами)
[1] Насон, Г. П. и Б. В. Сильверман. «Стационарное вейвлет-преобразование и некоторые статистические приложения». В «Вейвлетах и статистике» под редакцией Анестиса Антониадиса и Жоржа Оппенгейма, 103: 281-99. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.
[2] Койфман, Р. Р. и Д. Л. Донохо. «Перевод-инвариантное снятие шума». В «Вейвлетах и статистике» под редакцией Анестиса Антониадиса и Жоржа Оппенгейма 103: 125-50. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.
[3] Pesquet, J.-C., H. Krim и H. Carfantan. «Инвариантные во времени ортонормированные вейвлет-представления». Транзакции IEEE по обработке сигналов 44, № 8 (август 1996 года): 1964-70. https://doi.org/10.1109/78.533717.