Мы знаем, что классический DWT имеет недостаток: DWT не является инвариантным во времени преобразованием. Это означает, что даже при периодическом расширении сигнала DWT преобразованной версии сигнала X в общем случае не является преобразованной версией DWT из X.
Как восстановить инвариантность перевода, которая является желательным свойством, утраченным классическим DWT? Идея состоит в том, чтобы усреднить некоторые немного отличающиеся DWT, так называемые start-прореженные DWT, для определения стационарного вейвлет-преобразования (SWT). Это свойство полезно для нескольких приложений, таких как обнаружение точек распада.
Основное применение SWT - деноизирование. Для получения дополнительной информации об обосновании см. [CoiD95] в разделе Ссылки. Примеры см. в разделах 1-D Стационарное вейвлет-преобразование и 2-D Стационарное вейвлет-преобразование.
Принцип состоит в усреднении нескольких денозированных сигналов. Каждая из них получена с использованием обычной схемы деноизирования (см. Вейвлет деноизинг и непараметрическая оценка функции), но применена к коэффициентам δ-прореженного DWT.
Примечание
SWT определяется только для сигналов длиной, делимой на 2J, где J - максимальный уровень разложения. SWT использует периодические (per) внутренней линии.
Что такое DWT, децимированный (децимированный)?
Существует множество несколько различных способов обработки дискретного вейвлет-преобразования. Напомним, что базовым вычислительным шагом DWT является свертка, за которой следует прореживание. Прореживание сохраняет даже индексированные элементы.
Но прореживание можно было осуществить, выбрав нечетные индексированные элементы вместо даже индексированных элементов. Этот выбор касается каждого шага процесса разложения, поэтому на каждом уровне мы выбирали нечетный или четный.
Если мы выполняем все различные возможные разложения исходного сигнала, мы имеем 2J различные разложения, для данного максимального уровня J.
Обозначим с помощью δ j = 1 или 0 выбор нечётных или даже индексированных элементов на шаге j. Каждое разложение маркируется последовательностью 0s и 1s: start= ε1...,εJ. Это преобразование называется В-прореженным DWT.
Можно получить базисные векторы DWT, прореженные, из векторов стандартного DWT, применив сдвиг и соответствующий особому выбору начала координат базисных функций.
Существует возможность вычислить все δ-прореженные DWT для данного сигнала длиной N, вычисляя коэффициенты аппроксимации и детализации для каждой возможной последовательности start. Сделайте это, используя итеративно, слегка измененную версию базового шага DWT формы:
[A,D] = dwt(X,wname,'mode','per','shift',e);
Последние два аргумента указывают способ выполнения шага прореживания. Это классический для e = 0, но для e = 1 нечетные индексированные элементы сохраняются прореживанием.
Конечно, это нехороший способ вычислить все δ-прореженные DWT, потому что многие вычисления выполняются много раз. Теперь рассмотрим другой способ, который представляет собой стационарное вейвлет-преобразование (SWT).
Алгоритм SWT очень прост и близок к алгоритму DWT. Более точно, для уровня 1 все DWT-прореженные (только два на этом уровне) для данного сигнала могут быть получены путем свертки сигнала с соответствующими фильтрами, как в случае DWT, но без понижающей дискретизации. Тогда коэффициенты аппроксимации и детализации на уровне 1 имеют размер N, который является длиной сигнала. Это можно визуализировать на следующем рисунке.
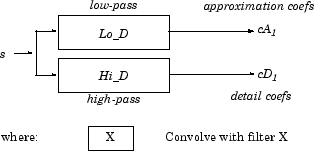
Общий этап j свертывает коэффициенты аппроксимации на уровне j-1 с усиленными вариантами соответствующих исходных фильтров для получения коэффициентов аппроксимации и детализации на уровне j. Это можно визуализировать на следующем рисунке.
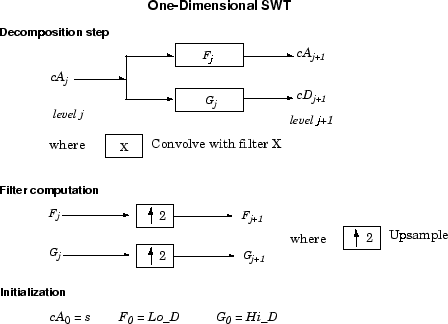
Далее, мы иллюстрируем, как извлечь данный δ-прореженный DWT из структуры коэффициентов приближения и детализации SWT.
Мы разложим последовательность чисел высоты с SWT, на уровне J = 3, используя ортогональный вейвлет.
Функция swt вычисляет последовательно следующие массивы, где A (j, α1,..., αj) или D (j, α1,..., αj) обозначает приближение или коэффициент детализации на уровне j, полученный для δ-децимированного DWT, характеризующегося
A (0) | A (0) | A (0) | A (0) | A (0) | A (0) | A (0) | A (0) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
A (1,0) | A (1,1) | A (1,0) | A (1,1) | A (1,0) | A (1,1) | A (1,0) | A (1,1) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) | D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) |
A (2,0,0) | A (2,1,0) | A (2,0,1) | A (2,1,1) | A (2,0,0) | A (2,1,0) | A (2,0,1) | A (2,1,1) |
D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) | D (1,0) | D (1,1) |
D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) | D (2,0,0) | D (2,1,0) | D (2,0,1) | D (2,1,1) |
D (3,0,0,0) | D (3,1,0,0) | D (3,0,1,0) | D (3,1,1,0) | D (3,0,0,1) | D (3,1,0,1) | D (3,0,1,1) | D (3,1,1,1) |
A (3,0,0,0) | A (3,1,0,0) | A (3,0,1,0) | A (3,1,1,0) | A (3,0,0,1) | A (3,1,0,1) | A (3,0,1,1) | A (3,1,1,1) |
Пусть j обозначает текущий уровень, где j также является текущим шагом алгоритма. Тогда у нас есть следующие абстрактные отношения с αi = 0 или 1:
[tmpAPP,tmpDET] = dwt(A(j,ε1, ,ɛj),wname,'mode','per','shift',ɛj+1); A(j+1,ɛ1, ,ɛj,ɛj+1) = circshift(tmpAPP,-ɛj+1); D(j+1,ɛ1, ,ɛj,ɛj+1) = circshift(tmpDET,-ɛj+1);
где circshift выполняет δ-круговой сдвиг входного вектора. Таким образом, если αj + 1 = 0, circshift команда неэффективна и может быть подавлена.
Пусть λ = [ε1,...,εJ] при αi = 0 или 1. Мы имеем 2J = 23 = восемь различных DWT, прореженных, на уровне 3. Выбирая start, мы можем извлечь из массива SWT соответствующий δ-прореженный DWT.
Теперь рассмотрим последний шаг, J = 3, и пусть [Cstart, L,] обозначает структуру вейвлет-декомпозиции, децимированную, для данного, Затем его можно извлечь из структуры разложения SWT, выбрав соответствующие коэффициенты следующим образом:
Cü =
A (3, α1, α2, α3) | D (3, (1), (2), (3) | D (2, (1), (2) | D (2, (1), (2) | D (1, α1) | D (1, α1) | D (1, α1) | D (1, α1) |
Lλ = [1,1,2,4,8]
Например, ε-decimated DWT соответствующий ε = [ε1, ε2, ε3] = [1,0,1] показывают в смелом в последовательности множеств предыдущего примера.
Это можно распространить на 2-D случай. Алгоритм стационарного вейвлет-преобразования для изображений визуализируется на следующем рисунке.
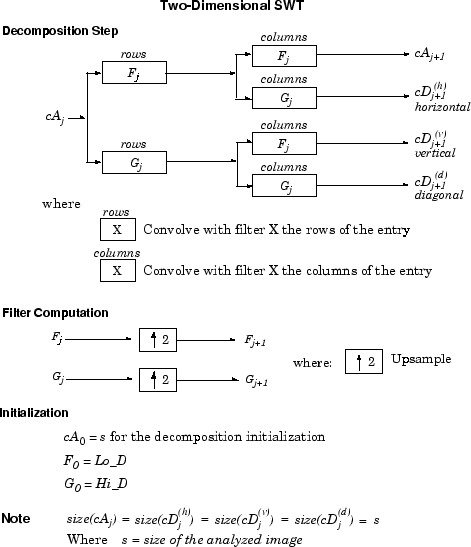
Каждый δ-прореженный DWT, соответствующий заданному start, может быть инвертирован.
Для восстановления исходного сигнала с помощью заданного, децимированного, DWT, характеризуемого [α1,..., αJ], мы можем использовать абстрактный алгоритм
FOR j = J:-1:1 A(j-1, ε1, ,ɛj-1) = ... idwt(A(j,ɛ1, ,ɛj),D(S,ɛ1, ,ɛj)],wname,'mode','per','shift',ɛj); END
Для каждого выбора start= (α1,..., αJ) получаем исходный сигнал A (0), начиная от несколько разных разложений, и улавливая по-разному основные особенности анализируемого сигнала.
Идея обратного дискретного стационарного вейвлет-преобразования состоит в том, чтобы усреднить обратные значения, полученные для каждого δ-прореженного DWT. Это можно сделать рекурсивно, начиная с уровня J до уровня 1.
ISWT получается со следующим абстрактным алгоритмом:
FOR j = J:-1:1
X0 = idwt(A(j,ɛ1, ,ɛj),D(j,ɛ1, ,ɛj)],wname, ...
'mode','per','shift',0);
X1 = idwt(A(j,ɛ1, ,ɛj),D(j,ɛ1, ,ɛj)],wname, ...
'mode','per','shift',1);
X1 = circshift(X1,-1);
A(j-1, ɛ1, ,ɛj-1) = (X0+X1)/2;
END
Таким же образом это можно распространить и на 2-D случай.
Некоторые полезные ссылки для стационарного вейвлет-преобразования (SWT) - [CoiD95], [NasS95] и [PesKC96] в ссылках.