В этом разделе рассматриваются функции дискретного стационарного вейвлет 1-D анализа с помощью программного обеспечения Wavelet Toolbox™. Дополнительные сведения см. в разделе Неразрешенные дискретные стационарные вейвлет-преобразования (SWT) в руководстве пользователя Wavelet Toolbox.
Панель инструментов обеспечивает эти функции для 1-D дискретного стационарного вейвлет-анализа. Дополнительные сведения о функциях см. на справочных страницах.
Имя функции | Цель |
|---|---|
Разложение |
Имя функции | Цель |
|---|---|
Реконструкция |
Структура стационарного вейвлет-разложения более прослеживаема, чем вейвлет-структура. Таким образом, утилиты, полезные для случая вейвлета, не являются необходимыми для стационарного вейвлет-преобразования (SWT).
В этом разделе вы научитесь
Загрузить сигнал
Выполнение стационарной вейвлет-декомпозиции сигнала
Построение аппроксимаций и деталей из коэффициентов
Отображение аппроксимации и подробных данных на уровне 1
Регенерация сигнала с помощью обратного стационарного вейвлет-преобразования
Выполнение многоуровневой стационарной вейвлет-декомпозиции сигнала
Реконструкция аппроксимации уровня 3
Реконструкция подробных данных уровней 1, 2 и 3
Реконструкция аппроксимаций уровня 1 и 2
Отображение результатов разложения
Восстановление исходного сигнала из разложения уровня 3
Удаление шума из сигнала
Поскольку анализ можно выполнять либо из командной строки, либо с помощью приложения Wavelet Analyzer, в этом разделе содержатся подразделы, охватывающие каждый метод.
В последнем подразделе рассматривается обмен информацией о сигналах и коэффициентах между диском и графическими инструментами.
Этот пример включает в себя шумный допплеровский тестовый сигнал.
Загрузите сигнал.
В подсказке MATLAB ® введите
load noisdopp
Задайте переменные. Напечатать
s = noisdopp;
Для SWT, если декомпозиция на уровне k требуется, 2^k должен равномерно разделяться на длину сигнала. Если исходный сигнал не имеет правильной длины, можно использовать wextend функция расширения.
Выполните одноуровневую стационарную вейвлет-декомпозицию.
Выполните одноуровневое разложение сигнала с помощью db1 вейвлет. Напечатать
[swa,swd] = swt(s,1,'db1');
При этом генерируются коэффициенты аппроксимации уровня 1 (swa) и детализации (swd). Оба имеют одинаковую длину с сигналом. Напечатать
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
noisdopp | 1x1024 | 8192 | double array |
s | 1x1024 | 8192 | double array |
swa | 1x1024 | 8192 | double array |
swd | 1x1024 | 8192 | double array |
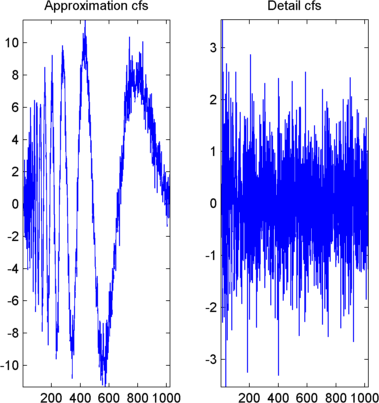
Отображение коэффициентов аппроксимации и детализации.
Для отображения коэффициентов аппроксимации и детализации на уровне 1 введите
subplot(1,2,1), plot(swa); title('Approximation cfs')
subplot(1,2,2), plot(swd); title('Detail cfs')
Регенерируйте сигнал с помощью обратного стационарного вейвлет-преобразования.
Чтобы найти обратное преобразование, введите
A0 = iswt(swa,swd,'db1');
Чтобы проверить идеальную реконструкцию, введите
err = norm(s-A0) err = 2.1450e-14
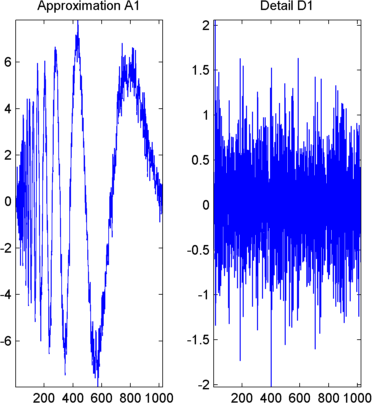
Построение и отображение аппроксимации и детализации из коэффициентов.
Для построения аппроксимации и детализации уровня 1 (A1 и D1) из коэффициентов swa и swd, тип
nulcfs = zeros(size(swa)); A1 = iswt(swa,nulcfs,'db1'); D1 = iswt(nulcfs,swd,'db1');
Для отображения аппроксимации и детализации на уровне 1 введите
subplot(1,2,1), plot(A1); title('Approximation A1');
subplot(1,2,2), plot(D1); title('Detail D1');
Выполните многоуровневую стационарную вейвлет-декомпозицию.
Для выполнения разложения на уровне 3 сигнала (снова с помощью db1 вейвлет), тип
[swa,swd] = swt(s,3,'db1');
Это генерирует коэффициенты аппроксимаций на уровнях 1, 2 и 3 (swa) и коэффициенты деталей (swd). Обратите внимание, что строки swa и swd имеют ту же длину, что и длина сигнала. Напечатать
clear A0 A1 D1 err nulcfs whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
noisdopp | 1x1024 | 8192 | double array |
s | 1x1024 | 8192 | double array |
swa | 3x1024 | 24576 | double array |
swd | 3x1024 | 24576 | double array |
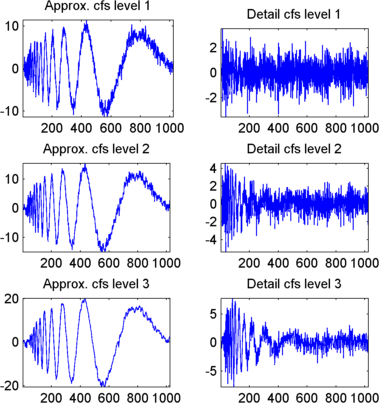
Отображение коэффициентов аппроксимаций и деталей.
Для отображения коэффициентов аппроксимаций и деталей введите
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(swa(i,:));
title(['Approx. cfs level ',num2str(i)])
subplot(3,2,kp+2), plot(swd(i,:));
title(['Detail cfs level ',num2str(i)])
kp = kp + 2;
end
Восстановить аппроксимацию на уровне 3 По коэффициентам.
Для восстановления аппроксимации на уровне 3 введите
mzero = zeros(size(swd)); A = mzero; A(3,:) = iswt(swa,mzero,'db1');
Реконструировать детали из коэффициентов.
Для восстановления подробных данных на уровнях 1, 2 и 3 введите
D = mzero;
for i = 1:3
swcfs = mzero;
swcfs(i,:) = swd(i,:);
D(i,:) = iswt(mzero,swcfs,'db1');
end
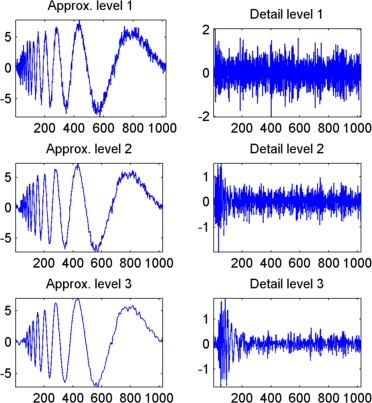
Реконструировать и отображать аппроксимации на уровнях 1 и 2 из аппроксимации на уровне 3 и детали на уровнях 2 и 3.
Для восстановления аппроксимаций на уровнях 2 и 3 введите
A(2,:) = A(3,:) + D(3,:); A(1,:) = A(2,:) + D(2,:);
Для отображения аппроксимаций и подробных данных на уровнях 1, 2 и 3 введите
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(A(i,:));
title(['Approx. level ',num2str(i)])
subplot(3,2,kp+2), plot(D(i,:));
title(['Detail level ',num2str(i)])
kp = kp + 2;
end
Удалите шум, установив пороговое значение.
Для отключения сигнала используйте ddencmp для вычисления глобального порога по умолчанию. Используйте wthresh чтобы выполнить фактическое пороговое значение коэффициентов детализации, а затем используйте команду iswt команду на получение денойзированного сигнала.
Примечание
Все методы для выбора порогов в 1-D Дискретной Небольшой волне Преобразовывают случай, также действительны для 1-D Постоянной Небольшой волны, Преобразовывают, которые являются также используемыми Аналитическим приложением Небольшой волны. Это также верно для 2-х преобразований.
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
Для отображения как исходного, так и денозированного сигнала введите
subplot(2,1,1), plot(s);
title('Original signal')
subplot(2,1,2), plot(clean);
title('denoised signal')
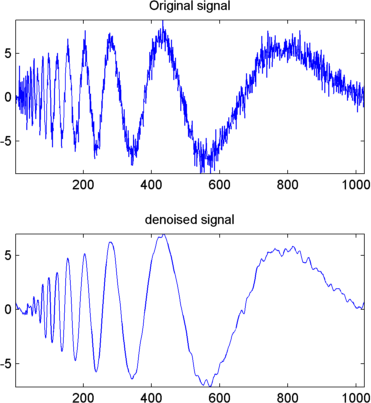
Полученный сигнал остается немного шумным. Результат может быть улучшен с учетом разложения s на уровне 5 вместо уровня 3 и повторяя этапы 14 и 15. Чтобы улучшить предыдущее деноизирование, введите
[swa,swd] = swt(s,5,'db1');
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
subplot(2,1,1), plot(s); title('Original signal')
subplot(2,1,2), plot(clean); title('denoised signal')
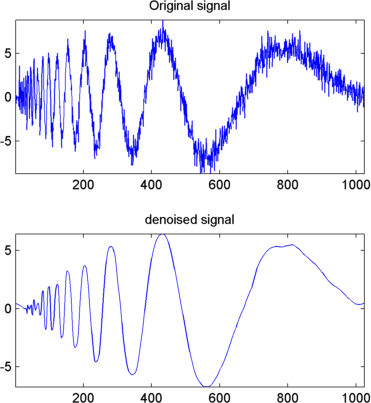
Второй синтаксис может использоваться для swt и iswt функции, дающие те же результаты:
lev = 5; swc = swt(s,lev,'db1'); swcden = swc; swcden(1:end-1,:) = wthresh(swcden(1:end-1,:),sorh,thr); clean = iswt(swcden,'db1');
Можно получить тот же график, используя те же команды графика, что и на шаге 16 выше.
Теперь мы исследуем стратегию обессмерчивания сигналов, основанную на 1-D стационарном вейвлет-анализе с использованием приложения вейвлет-анализатора. Основная идея состоит в том, чтобы усреднить множество немного различных дискретных вейвлет-анализов.
Запустите инструмент Denoising 1-D стационарного вейвлет-преобразования.
В приглашении MATLAB введите waveletAnalyzer.
Появится вейвлет-анализатор.
Выберите пункт меню SWT Denoising 1-D. Появляется средство дискретного стационарного вейвлет-преобразования для 1-D сигналов.
Загрузить данные.
В командной строке MATLAB введите
load noisbloc;
noisbloc переменная. Нажмите кнопку ОК, чтобы импортировать сигнал шумных блоков.Выполните декомпозицию стационарного вейвлета.
Выберите db1 вейвлет в меню Вейвлет и выберите 5 в меню Уровень, а затем нажмите кнопку Разложить сигнал. После паузы для вычисления инструмент отображает аппроксимацию стационарного вейвлета и коэффициенты детализации разложения. Они также называются недекимированными коэффициентами, поскольку они получены с использованием той же схемы, что и для DWT, но без шага прореживания (см. Алгоритм быстрого вейвлет-преобразования (FWT) в Руководстве пользователя Wavelet Toolbox).
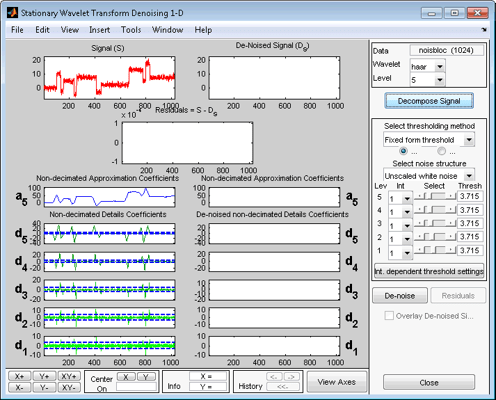
обнуление сигнала с помощью стационарного вейвлет-преобразования.
Несмотря на то, что имеется ряд опций для точной настройки алгоритма деноизирования, мы примем значения по умолчанию мягкого порогового значения фиксированной формы и нескрупулезного белого шума. Ползунки, расположенные в правой части окна, управляют зависящими от уровня порогами, обозначенными желтыми пунктирными линиями, проходящими горизонтально через графики коэффициентов детализации слева от окна. Желтые пунктирные линии также можно перетаскивать непосредственно с помощью левой кнопки мыши над графиками.
Следует отметить, что коэффициенты аппроксимации не имеют пороговых значений.
Нажмите кнопку «Denoise».
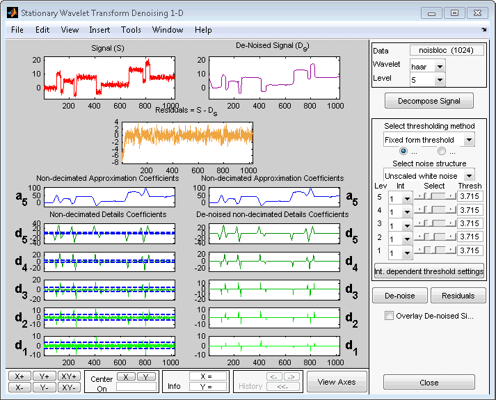
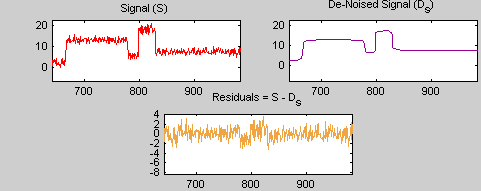
Результат вполне удовлетворительный, но, похоже, перемотан вокруг разрывов сигнала. Это можно увидеть, глядя на остатки и увеличивая точку пробоя, например, вокруг положения 800.
Выберите жесткий для режима пороговой обработки вместо мягкого, а затем нажмите кнопку denoise.
Результат хорошего качества, и остатки выглядят как образец белого шума. Чтобы исследовать этот последний момент, можно получить дополнительные сведения об остатках, нажав кнопку Остатки.
Инструмент позволяет сохранить сигнал на диске. Панель инструментов создает MAT-файл в текущей папке с выбранным именем.
Чтобы сохранить указанный выше сигнал, используйте пункт меню File > Save denoised Signal. Появится диалоговое окно, в котором можно указать папку и имя файла для хранения сигнала. Введите имя dnoibloc. После сохранения данных сигнала в файле dnoibloc.mat, загрузите переменные в рабочую область:
load dnoibloc whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
dnoibloc | 1x1024 | 8192 | double array |
thrParams | 1x5 | 580 | cell array |
wname | 1x3 | 6 | char array |
Денонсированный сигнал выдается dnoibloc. Кроме того, имеются параметры процесса обессоливания. Имя вейвлета содержится в wname:
wname
wname =
db1
и пороговые значения, зависящие от уровня, кодируются в thrParams, который является массивом ячеек длиной 5 (уровень разложения). Для i от 1 до 5, thrParams{i} содержит нижнюю и верхнюю границы интервала пороговой обработки и пороговое значение (поскольку допустимы пороговые значения, зависящие от интервала). Для получения дополнительной информации см. 1-D Адаптивную Пороговую обработку Коэффициентов Небольшой волны.
Например, для уровня 1,
thrParams{1}
ans =
1.0e+03 *
0.0010 1.0240 0.0041
Здесь нижняя граница равна 1, верхняя граница равна 1024, а пороговое значение равно 4.1. Общий интервал времени не сегментирован, и процедура не использует пороговые значения, зависящие от интервала.