В этом разделе рассматриваются функции анализа 1-D критическом образце с использованием программного обеспечения Wavelet Toolbox™.
Панель инструментов предоставляет эти функции для анализа 1-D сигналов. Дополнительные сведения см. на справочных страницах.
Имя функции | Цель |
|---|---|
Автоматическая денузация вейвлет-сигнала (рекомендуется) | |
Автоматическая шумоизоляция вейвлет-изображения (рекомендуется) | |
Пенализированный порог для вейвлет 1-D или 2-D деноизирования | |
Пороговые значения для вейвлет- 1-D с использованием стратегии Birgé-Massart | |
Вейвлет-денойзинг и сжатие | |
Автоматическая вейвлет-денойзинг | |
Диспетчер параметров порога |
В этом разделе вы узнаете, как
Загрузить сигнал
Выполнить одноуровневую вейвлет-декомпозицию сигнала
Построение аппроксимаций и деталей из коэффициентов
Отображение аппроксимации и подробных данных
Регенерация сигнала с помощью обратного вейвлет-преобразования
Выполнение многоуровневой вейвлет-декомпозиции сигнала
Извлечение коэффициентов приближения и детализации
Реконструкция аппроксимации уровня 3
Реконструкция подробных данных уровней 1, 2 и 3
Отображение результатов многоуровневой декомпозиции
Восстановление исходного сигнала из разложения уровня 3
Удаление шума из сигнала
Уточнение анализа
Сжатие сигнала
Отображение статистики и гистограмм сигнала
Поскольку анализ можно выполнять либо из командной строки, либо с помощью приложения Wavelet Analyzer, в этом разделе содержатся подразделы, охватывающие каждый метод.
В последнем подразделе рассматривается обмен информацией о сигналах и коэффициентах между диском и графическими инструментами.
Этот пример включает реальный сигнал - потребление электроэнергии, измеренное в течение 3 дней. Этот сигнал особенно интересен из-за шума, создаваемого при возникновении дефекта в контрольно-измерительном оборудовании при проведении измерений. Вейвлет-анализ эффективно удаляет шум.
Примечание
Чтобы скрыть сигнал, wdenoise и рекомендуется использовать денойзер вейвлет-сигнала.
Загрузите сигнал и выберите часть для вейвлет-анализа.
load leleccum;
s = leleccum(1:3920);
l_s = length(s);Выполните одноуровневую вейвлет-декомпозицию сигнала.
Выполните одноуровневое разложение сигнала с помощью db1 вейвлет.
[cA1,cD1] = dwt(s,'db1');При этом генерируются коэффициенты аппроксимации уровня 1 (cA1) и детали (cD1).
Построение аппроксимаций и деталей из коэффициентов.
Для построения аппроксимации и детализации уровня 1 (A1 и D1) из коэффициентов cA1 и cD1, тип
A1 = upcoef('a',cA1,'db1',1,l_s); D1 = upcoef('d',cD1,'db1',1,l_s);
или
A1 = idwt(cA1,[],'db1',l_s); D1 = idwt([],cD1,'db1',l_s);
Отображение аппроксимации и подробных данных.
Для отображения результатов декомпозиции первого уровня введите
subplot(1,2,1); plot(A1); title('Approximation A1') subplot(1,2,2); plot(D1); title('Detail D1')
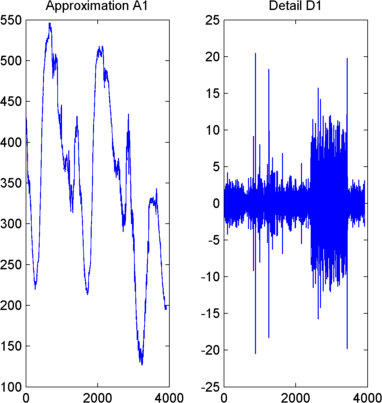
Регенерируйте сигнал с помощью обратного вейвлет-преобразования.
Чтобы найти обратное преобразование, введите
A0 = idwt(cA1,cD1,'db1',l_s);
err = max(abs(s-A0))Выполните многоуровневую вейвлет-декомпозицию сигнала.
Чтобы выполнить разложение сигнала уровня 3 (снова с помощью db1 вейвлет), тип
[C,L] = wavedec(s,3,'db1');Коэффициенты всех компонентов декомпозиции третьего уровня (то есть аппроксимации третьего уровня и первых трёх уровней детализации) возвращаются конкатенированными в один вектор, C. Вектор L даёт длины каждого компонента.
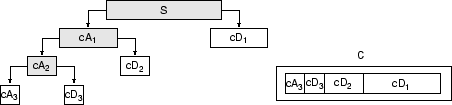
Извлеките коэффициенты приближения и детализации.
Извлечение коэффициентов аппроксимации уровня 3 из C, тип
cA3 = appcoef(C,L,'db1',3);
Извлечение коэффициентов детализации уровней 3, 2 и 1 C, тип
cD3 = detcoef(C,L,3); cD2 = detcoef(C,L,2); cD1 = detcoef(C,L,1);
или
[cD1,cD2,cD3] = detcoef(C,L,[1,2,3]);
Восстановите приближение уровня 3 и детали уровней 1, 2 и 3.
Восстановление аппроксимации уровня 3 из C, тип
A3 = wrcoef('a',C,L,'db1',3);
Для восстановления подробных данных на уровнях 1, 2 и 3 из C, тип
D1 = wrcoef('d',C,L,'db1',1);
D2 = wrcoef('d',C,L,'db1',2);
D3 = wrcoef('d',C,L,'db1',3);
Отображение результатов многоуровневой декомпозиции.
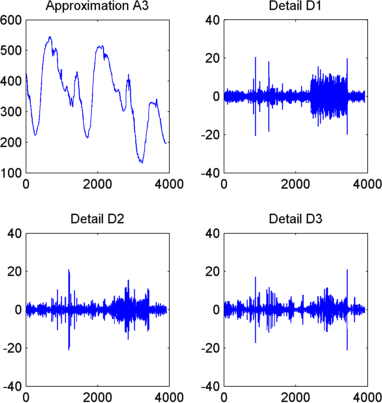
Для отображения результатов разложения уровня 3 введите
subplot(2,2,1); plot(A3);
title('Approximation A3')
subplot(2,2,2); plot(D1);
title('Detail D1')
subplot(2,2,3); plot(D2);
title('Detail D2')
subplot(2,2,4); plot(D3);
title('Detail D3')
Восстановите исходный сигнал из разложения уровня 3.
Чтобы восстановить исходный сигнал из структуры вейвлет-разложения, введите
A0 = waverec(C,L,'db1'); err = max(abs(s-A0))
Использование вейвлетов для удаления шума из сигнала требует идентификации того, какой компонент или компоненты содержат шум, и последующего восстановления сигнала без этих компонентов.
В этом примере мы отмечаем, что последовательные приближения становятся все менее и менее шумными, поскольку все больше и больше высокочастотной информации отфильтровывается из сигнала.
Приближение уровня 3, A3, является довольно чистым, как сравнение между ним и исходным сигналом.
Для сравнения аппроксимации с исходным сигналом введите
subplot(2,1,1);plot(s);title('Original'); axis off
subplot(2,1,2);plot(A3);title('Level 3 Approximation');
axis off
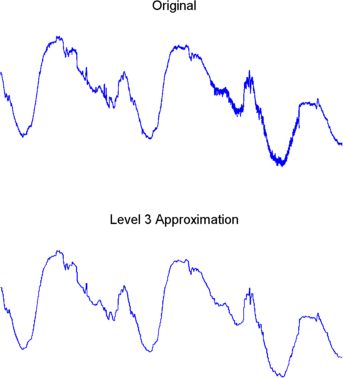
Конечно, отбрасывая всю высокочастотную информацию, мы также потеряли многие из самых острых характеристик исходного сигнала.
Оптимальное обесценение требует более тонкого подхода, называемого пороговым значением. Это предполагает отбрасывание только той части деталей, которая превышает определенный предел.
Удалите шум, установив пороговое значение.
Давайте еще раз посмотрим на детали нашего анализа уровня 3.
Для просмотра подробных данных D1, D2, и D3, тип
subplot(3,1,1); plot(D1); title('Detail Level 1'); axis off
subplot(3,1,2); plot(D2); title('Detail Level 2'); axis off
subplot(3,1,3); plot(D3); title('Detail Level 3'); axis off
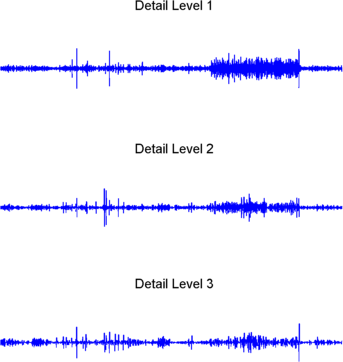
Большая часть шума возникает в последней части сигнала, где детали показывают их наибольшую активность. Что, если мы ограничим силу деталей, ограничив их максимальные значения? Это приведет к сокращению шума, оставляя детали незатронутыми в течение большей части их продолжительности. Но есть лучший способ.
Обратите внимание, что cD1, cD2, и cD3 являются только векторами MATLAB ®, поэтому мы могли бы непосредственно манипулировать каждым вектором, устанавливая каждый элемент в некоторую долю пикового или среднего значения векторов. Тогда мы могли бы реконструировать новые сигналы деталей D1, D2, и D3 из пороговых коэффициентов.
Для отключения сигнала используйте ddencmp для вычисления параметров по умолчанию и wdencmp команду для выполнения фактического сброса, наберите
[thr,sorh,keepapp] = ddencmp('den','wv',s);
clean = wdencmp('gbl',C,L,'db1',3,thr,sorh,keepapp);
Обратите внимание, что wdencmp использует результаты разложения (C и L), что мы уже рассчитали. Мы также уточняем, что мы использовали db1 вейвлет для выполнения исходного анализа, и мы задаем опцию глобального порогового значения 'gbl'. Посмотрите ddencmp и wdencmp для получения дополнительной информации об использовании этих команд см. справочные страницы.
Для отображения как исходного, так и денозированного сигнала введите
subplot(2,1,1); plot(s(2000:3920)); title('Original')
subplot(2,1,2); plot(clean(2000:3920)); title('denoised')
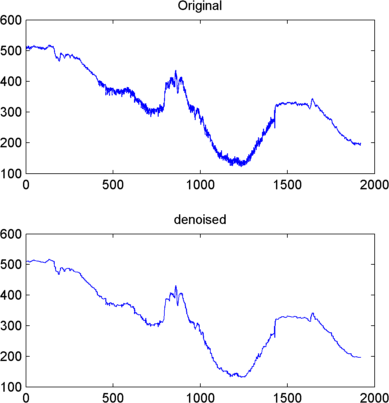
Мы построили здесь только шумную последнюю часть сигнала. Обратите внимание, как мы удалили шум, не нарушая четкую детализацию исходного сигнала. Это сила вейвлет-анализа.
Хотя использование функций командной строки для удаления шума из сигнала может быть громоздким, приложение Wavelet Analyzer программного обеспечения включает в себя простую в использовании функцию защиты от шума, которая включает автоматическое пороговое значение.
Более подробную информацию о процессе обезвреживания можно найти в следующих разделах:
Оценка вейвлет-деноизирующих и непараметрических функций в руководстве пользователя инструментария вейвлет
1-D Адаптивное пороговое значение дисперсии вейвлета в руководстве пользователя инструментария вейвлета
В этом разделе мы исследуем тот же электрический сигнал потребления, что и в предыдущем разделе, но мы используем приложение Wavelet Analyzer для анализа и устранения сигнала.
Примечание
Использование приложения Wavelet Analyzer для защиты от сигнала больше не рекомендуется. Вместо этого используйте Vavelet Signal Denoiser.
Запустите 1-D Wavelet Analysis Tool.
В приглашении MATLAB введите waveletAnalyzer.
Появится вейвлет-анализатор.
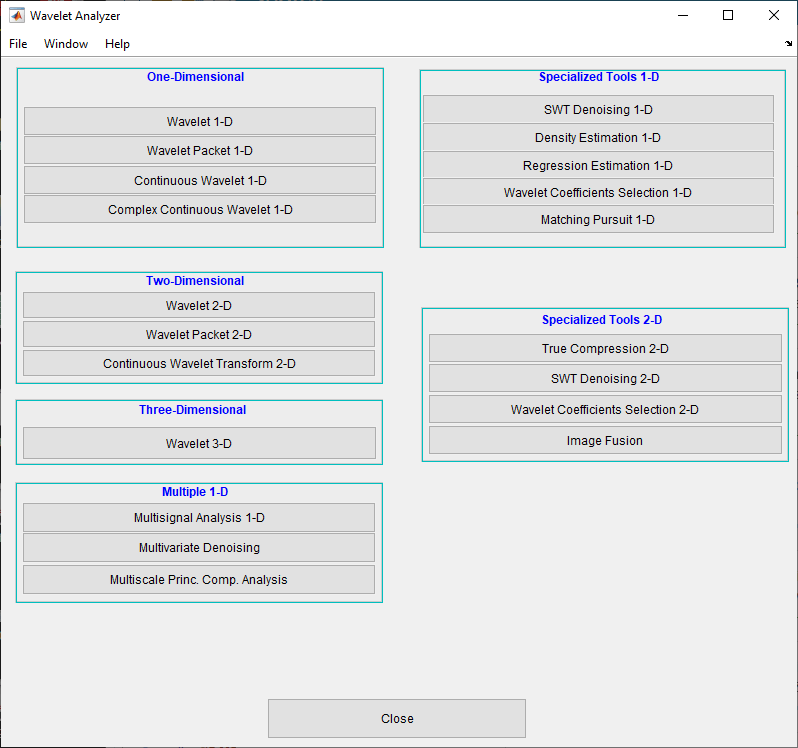
Выберите пункт меню Wavelet 1-D.
Появляется инструмент дискретного вейвлет-анализа для 1-D данных сигнала.
Загрузите сигнал.
В командной строке MATLAB введите
load leleccum;
leleccum переменная. Нажмите кнопку OK для импорта сигнала потребления электроэнергии.Выполните одноуровневую вейвлет-декомпозицию.
Чтобы начать наш анализ, давайте выполним одноуровневую декомпозицию с помощью db1 вейвлет, так же, как мы использовали функции командной строки в 1-D Анализ с помощью командной строки.
В правой верхней части инструмента Wavelet 1-D выберите db1 вейвлет и одноуровневая декомпозиция.
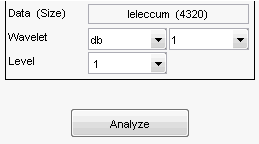
Нажмите кнопку «Анализ».
После паузы для вычисления инструмент отображает разложение.
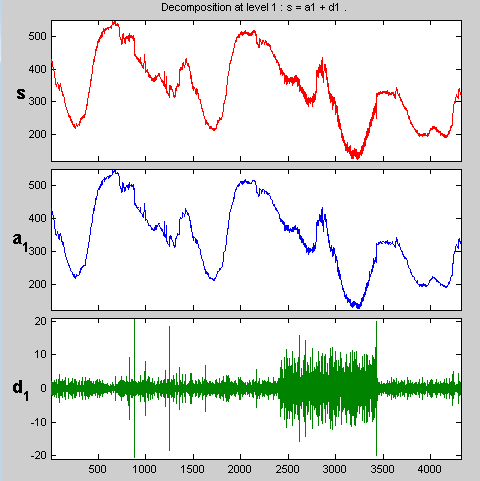
Увеличьте изображение соответствующей детали.
Одно из преимуществ использования приложения Wavelet Analyzer заключается в том, что вы можете легко увеличивать масштаб любой части сигнала и исследовать его более подробно.
Перетащите коробку с резиновой лентой (удерживая левую кнопку мыши) над частью сигнала, который требуется увеличить. Здесь мы выбрали шумную часть исходного сигнала.
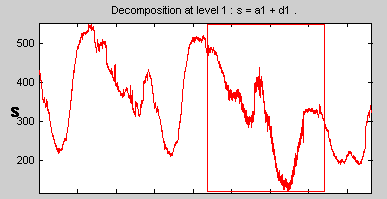
Нажмите кнопку X + (расположенную в нижней части экрана), чтобы увеличить изображение по горизонтали.
![]()
Инструмент Wavelet 1-D увеличивает масштаб всех отображаемых сигналов.
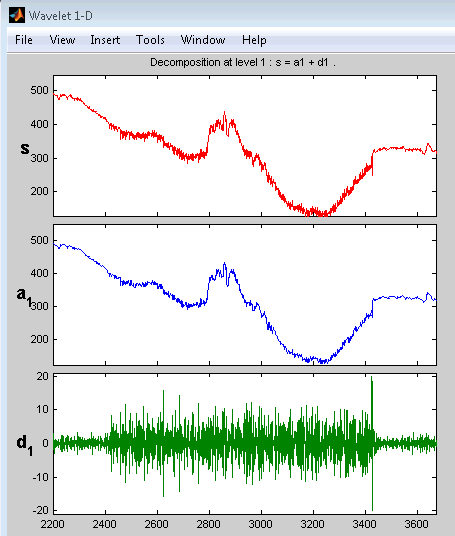
Другие элементы управления масштабированием делают более или менее то, что вы ожидаете от них. Например, кнопка X масштабируется по горизонтали. Функция хронологии отслеживает все ваши представления сигнала. Вернитесь к предыдущему уровню масштабирования, нажав кнопку со стрелкой влево.
Выполните многоуровневую декомпозицию.
Опять же, мы будем использовать графические инструменты, чтобы эмулировать то, что мы сделали в предыдущем разделе с помощью функций командной строки. Чтобы выполнить разложение сигнала уровня 3 с помощью db1 вейвлет:
Выберите 3 в меню «Уровень» в правом верхнем углу и снова нажмите кнопку «Анализ».

После выполнения разложения в инструменте Wavelet 1-D появится новый анализ.
Выбор различных видов декомпозиции
Меню режима отображения (среднее правое) позволяет выбирать различные виды вейвлет-декомпозиции.

Режим отображения по умолчанию называется «Режим полной декомпозиции». Другие альтернативы включают:
«Отдельный режим», который показывает детали и приближения в отдельных столбцах.
«Режим наложения», в котором отображаются детали на одном графике, наложенном разными цветами. Аппроксимации строятся аналогично.
«Tree Mode», который показывает дерево разложения, исходный сигнал и один дополнительный компонент по вашему выбору. Щелкните дерево разложения, чтобы выбрать компонент сигнала, который требуется просмотреть.
«Режим отображения и прокрутки», в котором отображаются три окна. Первый показывает исходный сигнал, наложенный на выбранное приближение. Во втором окне отображается выбранный элемент. Третье окно показывает вейвлет-коэффициенты.
«Show and Scroll Mode (Stem Cfs)» очень похож на «Show and Scroll Mode» за исключением того, что он отображает в третьем окне вейвлет-коэффициенты в виде стволовых графиков вместо цветных блоков.
Режим отображения по умолчанию можно изменять для каждого сеанса. Выберите требуемый режим в подменю «Вид» > «Режим отображения по умолчанию».
Примечание
Окна Сжатие (Compression) и Деноизирование (Denoising), открытые с помощью инструмента Wavelet 1-D, наследуют текущий атрибут визуализации коэффициента (стебли или цветные блоки).
В зависимости от выбранного режима отображения можно получить доступ к дополнительным параметрам отображения с помощью кнопки «Дополнительные параметры отображения».
Эти опции включают в себя возможность подавлять отображение различных компонентов и выбирать, отображать ли исходный сигнал вместе с деталями и приближениями.
Удалите шум из сигнала.
Приложение Wavelet Analyzer имеет функцию отрицания с предопределенной стратегией пороговой обработки. Это очень облегчает удаление шума из сигнала.
Примечание
Более не рекомендуется использовать опцию «denoising». Вместо этого используйте Vavelet Signal Denoiser.
Вызовите инструмент «Denoising»: нажмите кнопку «Denoise», расположенную посередине справа от окна, под кнопкой «Analyze».
Появится окно Wavelet 1-D Denoising.
Несмотря на то, что имеется ряд опций для точной настройки алгоритма деноизирования, мы примем значения по умолчанию для мягкого порогового значения фиксированной формы и нескрупулезного белого шума. Unscaled white noise параметр соответствует установке входного аргумента мультипликативного порога SCAL из wden кому 'one'. Выбор Scaled white noise соответствует 'sln', и Non-white noise соответствует 'mln'. Дополнительные сведения см. в разделе wden.
Для продолжения нажмите кнопку «Denoise».
Денозированный сигнал оказывается наложенным на оригинал. Инструмент также отображает вейвлет-коэффициенты обоих сигналов. Исходные коэффициенты детализации отображаются в левой части экрана. Чтобы выровнять по времени уровни разложения по всем масштабам, вейвлет-коэффициенты реплицируются в каждой шкале для учета недостающих временных точек. Следовательно, по мере того, как масштаб становится более грубым, коэффициенты принимают вид лестницы.
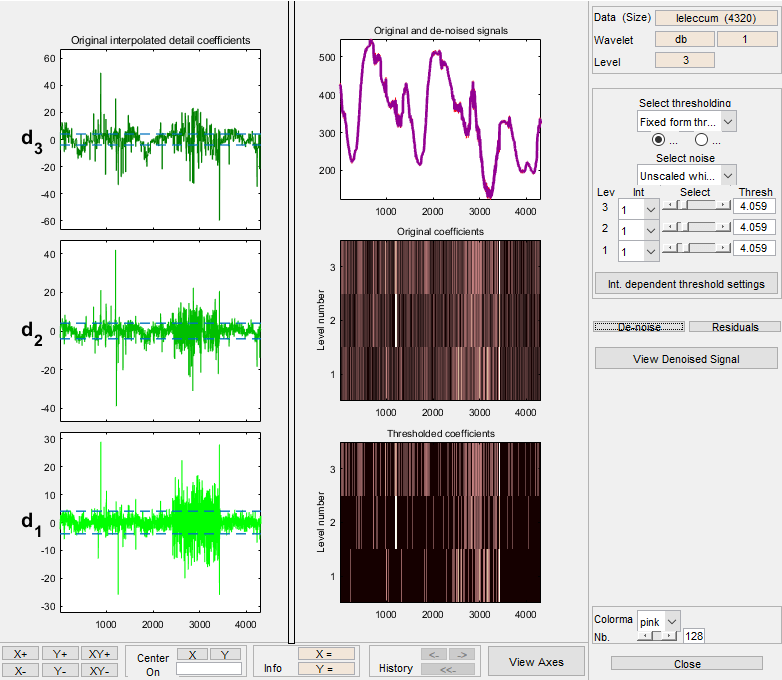
Увеличьте график исходного и деноизированного сигналов для более внимательного просмотра.
Перетащите рамку с резиновой лентой вокруг соответствующей области и нажмите кнопку XY +.
Дурацкое окно увеличивает вид. По умолчанию исходный сигнал отображается красным цветом, а деноизированный - желтым.
Закройте окно Wavelet 1-D Denoising: нажмите кнопку Close.
Окна Denoise и Compression нельзя открыть одновременно, поэтому закройте окно Wavelet 1-D Denoising для продолжения. При появлении диалогового окна «Обновление синтезированного сигнала» нажмите кнопку «Нет». Если нажать «Да», синтезированный сигнал будет доступен в главном окне Wavelet 1-D.
Уточните анализ.
Графические инструменты упрощают уточнение анализа в любое время. До сих пор мы рассматривали анализ уровня 3 с использованием db1. Давайте уточним наш анализ сигнала электрического потребления, используя db3 вейвлет на уровне 5.
Выберите 5 в меню «Уровень» в правом верхнем углу и выберите db3 из меню «Вейвлет». Нажмите кнопку «Анализ».
Сжать сигнал.
Инструменты графического интерфейса имеют опцию сжатия с автоматическим или ручным порогом.

Откройте окно Сжатие: нажмите кнопку Сжатие, расположенную в середине справа от окна, под кнопкой Анализ.
Появится окно Сжатие (Compression).
Хотя у вас всегда есть возможность выбора по пороговому уровню, здесь мы воспользуемся функцией глобального порогового уровня для быстрого и простого сжатия.
Примечание
Если вы хотите экспериментировать с ручным пороговым значением, выберите опцию По пороговому значению уровня (By Level thresholding) в меню, расположенном в правом верхнем углу окна Wavelet 1-D Compression. Ползунки, расположенные под этим меню, затем управляют зависящими от уровня порогами, обозначенными желтыми пунктирными линиями, проходящими горизонтально через графики в левой части окна. Желтые пунктирные линии также можно перетаскивать непосредственно с помощью левой кнопки мыши.
Нажмите кнопку «Сжатие», расположенную справа в центре.
После паузы для вычислений сигнал потребления электроэнергии снова отображается красным цветом, а сжатый вариант - желтым. Ниже мы увеличили масштаб, чтобы поближе взглянуть на шумную часть сигнала.
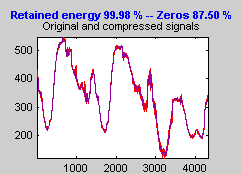
Видно, что процесс сжатия удалил большую часть шума, но сохранил 99,99% энергии сигнала.
В инструменте «Вейвлет 1-D Сжатие» нажмите кнопку «Остатки». Появится окно More on Reseives for Vavelet 1-D Compression.
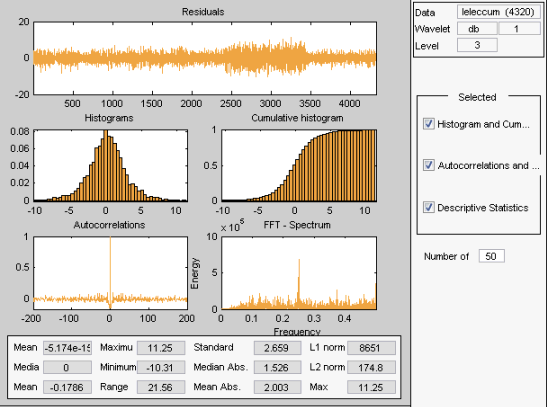
Отображаемая статистика включает в себя показатели тенденции (среднее, режим, медиана) и дисперсии (диапазон, стандартное отклонение). Кроме того, инструмент предоставляет частотно-распределительные диаграммы (гистограммы и кумулятивные гистограммы), а также временные диаграммы: автокорреляционная функция и спектр. Та же функция существует для инструмента Wavelet 1-D Denoising.
Закройте окно Wavelet 1-D Compression: нажмите кнопку Close. При появлении диалогового окна «Обновление синтезированного сигнала» нажмите кнопку «Нет».
Показать статистику.
Можно просмотреть различные статистические данные о сигнале и его компонентах.
В инструменте Wavelet 1-D нажмите кнопку Статистика.

Появится окно Wavelet 1-D Statistics, в котором по умолчанию отображается статистика исходного сигнала.
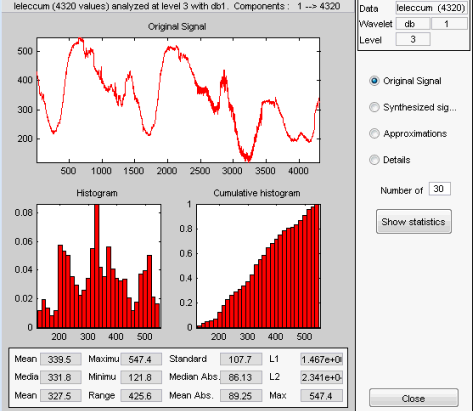
Выберите синтезированный сигнал или компонент сигнала, статистику которого требуется изучить. Нажмите соответствующую кнопку и нажмите кнопку Показать статистику. Здесь мы выбрали анализ синтезированного сигнала с использованием 100 ячеек вместо 30, что является значением по умолчанию:
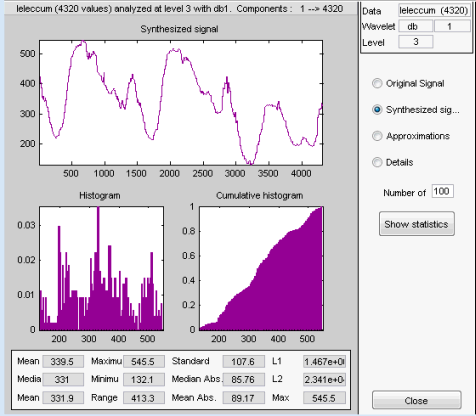
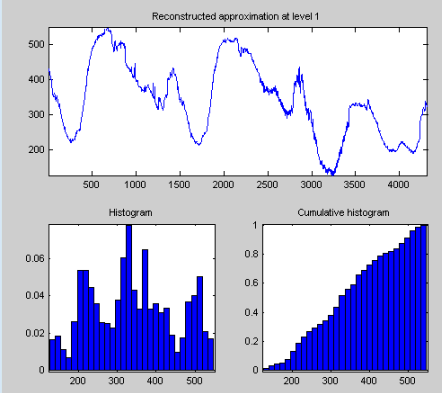
Отображаемая статистика включает в себя показатели тенденции (среднее, режим, медиана) и дисперсии (диапазон, стандартное отклонение).
Кроме того, инструмент предоставляет частотно-распределительные диаграммы (гистограммы и кумулятивные гистограммы). Эти гистограммы можно построить отдельно с помощью кнопки Гистограммы в окне 1-D вейвлетов.
Нажмите кнопку «Аппроксимация». Появится меню, в котором можно выбрать уровень приближения, который требуется изучить.
Выберите Уровень 1 и снова нажмите кнопку Показать статистику. Появляется статистика для аппроксимации уровня 1.
Графический интерфейс Wavelet 1-D позволяет импортировать информацию с диска и рабочей области MATLAB и экспортировать ее.
Можно сохранить синтезированные сигналы, коэффициенты и декомпозиции из инструмента Wavelet 1-D на диск, где информация может быть обработана и затем повторно загружена в графический инструмент.
Сохранение синтезированных сигналов. Можно обработать сигнал в инструменте Wavelet 1-D, а затем сохранить обработанный сигнал в MAT-файл (с расширением mat или другое).
Например, загрузите пример анализа: File > Example Analysis > Basic Signals > с db3 на уровне 5 → Sum of sines и выполните операцию сжатия или обессоливания исходного сигнала. При закрытии окна Деноизирование (Denoising) или Сжатие (Compression) обновите синтезированный сигнал, нажав кнопку Да (Yes) в диалоговом окне.
Затем в инструменте «Вейвлет 1-D» выберите пункт меню «Файл» > «Сохранить» > «Сигнал».
Появится диалоговое окно, позволяющее выбрать папку и имя файла для MAT-файла. В этом примере выберите имя synthsig.
Чтобы загрузить сигнал в рабочее пространство, просто введите
load synthsig;
Когда синтезированный сигнал получен с использованием любого метода пороговой обработки, за исключением глобального, сохраненная структура является
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
synthsig | 1x1000 | 8000 | double множество |
thrParams | 1x5 | 580 | cell array |
wname | 1x3 | 6 | char array |
Синтезированный сигнал задается переменной synthsig. Кроме того, параметры процесса денойзинга или сжатия задаются именем вейвлета (wname) и пороговые значения, зависящие от уровня, содержащиеся в thrParams переменная, которая представляет собой массив ячеек длиной 5 (такой же, как уровень разложения).
Для i от 1 до 5, thrParams{i} содержит более низкие и верхние границы интервала пороговой обработки и порогового значения (так как пороги иждивенца интервала позволены, см. 1-D Адаптивную Пороговую обработку Коэффициентов Небольшой волны).
Например, для уровня 1,
thrParams{1}
ans =
1.0e+03 *
0.0010 1.0000 0.0014
Когда синтезированный сигнал получен с использованием глобального метода пороговой обработки, сохраненной структурой является
| Имя | Размер | Байты | Класс |
|---|---|---|---|
synthsig | 1x1000 | 8000 | double array |
valTHR | 1x1 | 8 | double array |
wname | 1x3 | 6 | char array |
где переменная valTHR содержит глобальный порог:
valTHR
valTHR =
1.2922
Сохранение коэффициентов дискретного вейвлет-преобразования. Инструмент Wavelet 1-D позволяет сохранить коэффициенты дискретного вейвлет-преобразования (DWT) на диске. Панель инструментов создает MAT-файл в текущей папке с выбранным именем.
Чтобы сохранить коэффициенты DWT из текущего анализа, используйте пункт меню «Файл» > «Сохранить» > «Коэффициенты».
Появится диалоговое окно, в котором можно указать папку и имя файла для хранения коэффициентов.
Рассмотрим пример анализа:
Файл> Анализ В качестве примера> Базовые сигналы> с db1 на уровне 5 → кривая Регента.
После сохранения вейвлет-коэффициентов в файл cantor.mat, загрузите переменные в рабочую область:
load cantor whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x2190 | 17520 | double array |
longs | 1x7 | 56 | double array |
thrParams | 0x0 | 0 | double array |
wname | 1x3 | 6 | char array |
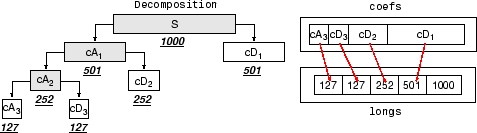
Переменная coefs содержит дискретные вейвлет-коэффициенты. Точнее, в приведенном выше примере coefs является вектором 1 на 2190 конкатенированных коэффициентов, и longs - вектор, задающий длины каждого компонента coefs.
Переменная wname содержит имя вейвлета и thrParams пуст, так как синтезированный сигнал не существует.
Сохранение разложений. Инструмент Wavelet 1-D позволяет сохранить весь набор данных из дискретного вейвлет-анализа на диск. Панель инструментов создает MAT-файл в текущей папке с выбранным именем, за которым следует расширение wa1 (вейвлет-анализ 1-D).
Откройте инструмент Wavelet 1-D и загрузите пример анализа:
Файл > Пример анализа > Основные сигналы > с db3 на уровне 5 → Сумма синусов
Чтобы сохранить данные из этого анализа, используйте пункт меню Файл > Сохранить > Декомпозиция.
Появится диалоговое окно, в котором можно указать папку и имя файла для хранения данных разложения. Введите имя wdecex1d.
После сохранения данных разложения в файл wdecex1d.wa1, загрузите переменные в рабочую область:
load wdecex1d.wa1 -mat whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x1023 | 8184 | double array |
data_name | 1x6 | 12 | char array |
longs | 1x7 | 56 | double array |
thrParams | 0x0 | 0 | double array |
wave_name | 1x3 | 6 | char array |
Примечание
Опции сохранения также доступны при выполнении деноизирования или сжатия в инструменте Wavelet 1-D. В окне Wavelet 1-D Denoising можно сохранить деноизированный сигнал и разложение. То же самое справедливо для окна Wavelet 1-D Compression. Таким образом, можно сохранить множество различных испытаний из окон Denoising и Compression, не возвращаясь к главному окну Wavelet 1-D во время процесса точной настройки.
Примечание
При сохранении синтезированного сигнала, разложения или коэффициентов в MAT-файл, mat расширение файла не требуется. Аппроксимации можно сохранять отдельно для каждого уровня или сохранять их все одновременно.
Инструмент Wavelet 1-D позволяет экспортировать 1-D вейвлет-анализ в рабочую область MATLAB в различных форматах.
Например, загрузите пример анализа для freqbrk сигнал.
После выполнения вейвлет 1-D анализа нагрузок выберите File —> Export to Workspace.
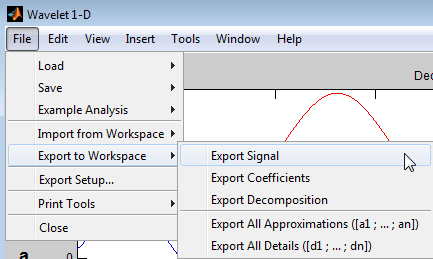
У вас есть возможность
Export Signal - Эта опция экспортирует вектор синтезированного сигнала.
Export Coefficients - Эта опция экспортирует вектор коэффициентов вейвлета и масштабирования, вектор бухгалтерского учета и анализирующий вейвлет в структурном массиве. Вейвлет и коэффициент масштабирования и векторы бухгалтерского учета идентичны выходному сигналу wavedec.
Export Decomposition - Эта опция идентична Export Coefficients за исключением того, что он также содержит имя анализируемого сигнала.
Export All Approximations - Эта опция экспортирует матрицу L-на-N, где L - значение Level, а N - длина входного сигнала. Каждая строка матрицы является проекцией на аппроксимационное пространство на соответствующем уровне. Например, первая строка матрицы является проекцией на аппроксимационное пространство на уровне 1.
Export All Details - Эта опция экспортирует матрицу L-на-N, где L - значение Level, а N - длина входного сигнала. Каждая строка матрицы является проекцией на детальное (вейвлет) пространство на соответствующем уровне. Например, первая строка матрицы является проекцией на пространство деталей на уровне 1.
В приложение Wavelet Analyzer можно загружать сигналы, коэффициенты или декомпозиции. Загружаемая информация, возможно, была ранее экспортирована из приложения, а затем обработана в рабочей области, или же она была первоначально сгенерирована из командной строки.
В любом случае необходимо соблюдать строгие форматы файлов и структуры данных, используемые инструментом Wavelet 1-D, иначе при попытке загрузить информацию возникнут ошибки.
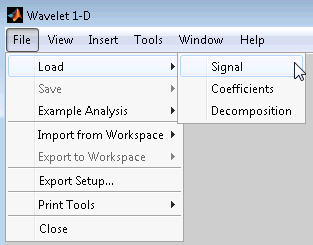
Загрузка сигналов. Чтобы загрузить сигнал, созданный в рабочем пространстве MATLAB, в инструмент Wavelet 1-D, сохраните сигнал в MAT-файле (с расширением mat или другое).
Например, предположим, что вы разработали сигнал под названием warma и хотите проанализировать его с помощью инструмента Wavelet 1-D.
save warma warma
Переменная рабочей области warma должна быть вектором.
sizwarma = size(warma)
sizwarma =
1 1000
Чтобы загрузить этот сигнал в инструмент Wavelet 1-D, используйте пункт меню File > Load > Signal.
Появится диалоговое окно, в котором можно выбрать соответствующий файл MAT для загрузки.
Примечание
Первая 1-D переменная, обнаруженная в файле, считается сигналом. Проверка переменных производится в алфавитном порядке.
Загрузка коэффициентов дискретного вейвлет-преобразования. Чтобы загрузить дискретные коэффициенты вейвлет-преобразования в инструмент вейвлет- 1-D, необходимо сначала сохранить соответствующие данные в MAT-файле, который должен содержать по крайней мере две переменные coefs и longs.
Переменная coefs должен быть вектором коэффициентов DWT (сцепленных для различных уровней) и переменной longs вектор, задающий длину каждого компонента coefs, а также длину исходного сигнала.
После создания или редактирования соответствующих данных в рабочей области введите
save myfile coefs longs
Команда меню «Файл» > «Загрузка» > «Коэффициенты» инструмента «Вейвлет 1-D» используется для загрузки данных в графический инструмент.
Появится диалоговое окно, в котором можно выбрать папку и файл, в которых находятся данные.
Загрузка декомпозиций. Чтобы загрузить данные декомпозиции дискретного вейвлет-преобразования в графический интерфейс вейвлет- 1-D, необходимо сначала сохранить соответствующие данные в MAT-файле (с расширением wa1 или другое).
MAT-файл содержит следующие переменные.
| Переменная | Статус | Описание |
|---|---|---|
coefs | Необходимый | Вектор конкатенированных коэффициентов DWT |
longs | Необходимый | Вектор, задающий длины компонентов |
wave_name | Необходимый | Символьный вектор, определяющий имя вейвлета, используемого для разложения (например, |
data_name | Дополнительный | Символьный вектор, указывающий имя разложения |
После создания или редактирования соответствующих данных в рабочей области введите
save myfile coefs longs wave_name
Команда меню «Файл» > «Загрузка» > «Декомпозиция» инструмента «Вейвлет 1-D» используется для загрузки данных декомпозиции в графический инструмент.
Появится диалоговое окно, в котором можно выбрать папку и файл, в которых находятся данные.
Примечание
При загрузке сигнала, разложения или коэффициентов из MAT-файла расширение этого файла является свободным. mat расширение не требуется.
Денойзер вейвлет-сигнала | wdenoise