Communications Toolbox™ предоставляет источники, раковины и устройства отображения, которые облегчают анализ производительности системы связи.
Используйте функции и блоки, перечисленные в Sources and Sinks, чтобы сгенерировать случайные данные для симуляции источника сигнала.
Случайные символы
The randsrc функция генерирует случайные матрицы, записи которых выбираются независимо от заданного алфавита с заданным распределением. Специальный случай генерирует биполярные матрицы.
Например, команда ниже генерирует матрицу 5 на 4, записи которой случайны, независимо выбраны и равномерно распределены в наборе {1,3,5}.
a = randsrc(5,4,[1,3,5])
a = 5×4
5 1 1 1
5 1 5 3
1 3 5 5
5 5 3 5
3 5 5 5
Чтобы наклонить распределение так, чтобы 1 было в два раза чаще, чем 3 или 5, используйте команду ниже. Третий входной параметр имеет две строки, одна из которых указывает возможные значения b а другой указывает вероятность каждого значения.
b = randsrc(5,4,[1,3,5; .5,.25,.25])
b = 5×4
3 5 3 5
1 3 1 3
5 1 1 1
5 3 1 5
3 1 1 1
Случайные целые числа
В MATLAB ® randi функция генерирует случайные целочисленные матрицы, записи которых находятся в заданной области значений. Специальный случай генерирует случайные двоичные матрицы.
Например, команда ниже генерирует матрицу 5 на 4, содержащую случайные целые числа от 2 до 10.
c = randi([2,10],5,4)
c = 5×4
5 6 4 6
5 6 8 10
8 7 7 5
9 8 3 7
3 8 3 4
Если желаемую область значений значений [0,10] вместо [2,10], можно использовать любую из приведенных ниже команд. Они дают различные числовые результаты, но используют одно и то же распределение.
d = randi([0,10],5,4); e = randi([0 10],5,4);
В Simulink ® генератор случайных целых чисел и генератор Пуассона генерируют векторы, содержащие случайные неотрицательные целые числа. Блок Генератора Случайных Целых Чисел использует равномерное распределение в ограниченной области значений, которое вы задаете в маске блока. Блок Генератора Целого числа Пуассона использует распределение Пуассона, чтобы определить его выходом. В частности, выход может включать любое неотрицательное целое число.
Шаблоны случайных битовых ошибок
В MATLAB randerr функция генерирует матрицы, значения которых равны 0 или 1. Однако его варианты отличаются от опций randi, потому что randerr предназначен для проверки кодирования управления ошибками. Например, команда ниже генерирует двоичную матрицу 5 на 4, где каждая строка содержит в точности один 1.
f = randerr(5,4)
f = 5×4
0 0 0 1
1 0 0 0
1 0 0 0
0 0 1 0
0 0 0 1
Можно использовать такую команду, чтобы возмущать двоичный код, который состоит из пяти четырехбитных кодовых слов. Добавление случайной матрицы f в вашу матрицу кода (по модулю 2) вводит ровно одну ошибку в каждое кодовое слово.
С другой стороны, чтобы возмущать каждое кодовое слово путем введения одной ошибки с вероятностью 0,4 и двух ошибок с вероятностью 0,6, используйте команду ниже. Каждая строка имеет один '1' с вероятностью 0,4, в противном случае два '1' s
g = randerr(5,4,[1,2; 0.4,0.6])
g = 5×4
1 0 1 0
0 1 0 1
0 0 0 1
1 0 0 1
0 0 1 0
Добавление случайной матрицы g в вашу матрицу кода (по модулю 2) вводит одну или две ошибки в каждое кодовое слово с заданной вероятностью вхождения для каждого. Матрица вероятностей, которая является третьим аргументом randerr влияет только на количество 1с в каждой строке, а не на их размещение.
В качестве другого приложения можно сгенерировать equiprobable двоичный 100-элементный вектор-столбец с помощью любой из приведенных ниже команд. Эти три команды формируют различные числовые выходы, но используют одно и то же распределение. Третьи входные параметры варьируются в зависимости от конкретного способа определения поведения каждой функции.
binarymatrix1 = randsrc(100,1,[0 1]); % Possible values are 0,1 binarymatrix2 = randi([0 1],100,1); % Two possible values binarymatrix3 = randerr(100,1,[0 1; 0.5 0.5]); % No 1s, or one 1
В Simulink блок Binary Generator Бернулли генерирует случайные биты и подходит для представления источников. Блок рассматривает каждый элемент сигнала как независимую случайную переменную Бернулли. Кроме того, различные элементы не должны быть одинаково распределены.
Создайте блоки генератора шума в Simulink® для моделирования ссылок связи.
Можно создать генераторы случайных шумов для симуляции шума в канале с помощью блока MATLAB Function (Simulink) с функциями генерации случайных чисел. Создайте различные типы шума канала с помощью следующих комбинаций.
| Распределение | Блок | Функция |
|---|---|---|
| Гауссовский | MATLAB Function (Simulink) | wgn |
| Рэлей | MATLAB Function (Simulink) | randn |
| Rician | MATLAB Function (Simulink) | randn |
| Равномерность на ограниченном интервале | MATLAB Function (Simulink) | rand |
Пример создания распределенного шума Релея и Райса см. в Simulink.
В MATLAB ® wgn функция генерирует случайные матрицы, используя белое Гауссово шумовое распределение. Степень шума задается либо в дБВ (децибелы относительно ватта), либо в дБм, либо в линейных модулях. Можно сгенерировать как реальный, так и сложный шум.
Для примера команда ниже генерирует вектор-столбец длины 50, содержащую настоящий белый Гауссов шум, степень которого равна 2 дБВ. По умолчанию тип степени в дБВ и импедансе нагрузки составляет 1 Ом.
y1 = wgn(50,1,2);
Чтобы сгенерировать комплексный белый Гауссов шум, степень которого составляет 2 Вт, через нагрузку в 60 Ом, используйте любую из приведенных ниже команд.
y2 = wgn(50,1,2,60,'complex','linear'); y3 = wgn(50,1,2,60,'linear','complex');
Чтобы передать сигнал через аддитивный канал белого Гауссова шума, используйте awgn функция. Для получения дополнительной информации см. раздел «Канал AWGN».
Используйте функции, Системные объекты и блоки, перечисленные в Источниках и Приемниках, чтобы сгенерировать последовательности для расширения или синхронизации в системе связи. Можно сгенерировать псевдослучайные последовательности, коды синхронизации и ортогональные коды. Для примеров, сравнивающих корреляционные свойства этих генераторов последовательности, см. «Расширяющиеся последовательности».
Можно сгенерировать псевдослучайные или псевдослучайные (PN) последовательности, используя эти системные объекты в MATLAB® и эти блоки в Simulink. Применения этих последовательностей варьируются от систем связи с расширенным спектром с множественным доступом до диапазона, синхронизации и скремблирования данных.
| Последовательность | Системные object™ | Блок |
|---|---|---|
| Последовательности Голда | comm.GoldSequence | Gold Sequence Generator |
| Последовательности Касами | comm.KasamiSequence | Kasami Sequence Generator |
| Псевдошумовые последовательности | comm.PNSequence | PN Sequence Generator |
Чтобы сгенерировать псевдослучайные последовательности, базовый код реализует регистры сдвига, как показано на этой схеме.
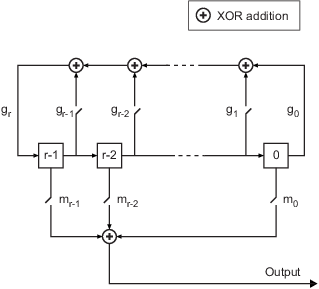
Все регистры r в генераторе обновляют свои значения на каждом временном шаге в соответствии со значением входящей стрелы к регистру сдвига. Сумматоры выполняют сложение по модулю 2. Регистр сдвига может быть описан двоичным полиномом в z, g r zr + gr-1 zr-1 +... + <reservedrangesplaceholder1> 0. Коэффициент i g 1, если есть связь, или 0, если нет связи, от i-го регистра сдвига до сумматора.
Коэффициент m i равен 1, если есть задержка, или 0, если нет задержки, от i-го регистра сдвига до сумматора, предшествующего выходу. Если сдвиг равен нулю, m 0 переключатель закрывается, в то время как все другие переключатели m k открыты.
Генераторы Касами и псевдошумовая последовательность используют это полиномиальное описание для своего полинома генератора. Генератор последовательности Голда использует это полиномиальное описание для предпочтительных первой и второй полиномиальных псевдошумовые последовательности генератора.
Этот пример показывает, что последовательности выходят из PN Sequence Generator может быть смоделирован с помощью линейного регистра сдвига с обратной связью (LFSR), созданного с помощью примитивных блоков Simulink ®.

Для выбранного полинома генератора, p (z) = z ^ 6 + z + 1, модель генерирует псевдошумовую последовательность периодов 63, используя PN Sequence Generator блок и путем моделирования LFSR с использованием примитивных блоков Simulink. Два параметра, Initial states и Output mask vector (or scalar shift value), интерпретируются в схеме модели LFSR. The PreLoadFcn функция обратного вызова используется для инициализации параметров во время выполнения. Чтобы просмотреть функции обратного вызова, перейдите к MODELING> SETUP> Model Settings> Model Properties, и выберите Callbacks вкладка.
Выходные возможности показов двух реализаций дают совпадающие псевдошумовые последовательности.

Использование блока Псевдошумовой последовательности Generator позволяет вам легко сгенерировать псевдошумовые последовательности больших периодов. Чтобы экспериментировать дальше, откройте модель. Измените настройки, чтобы увидеть, как изменяется эффективность для различных задержек пути или настройте параметры генератора псевдошумовой последовательности. Можно экспериментировать с различными начальными состояниями, изменяя значение начальных состояний перед выполнением симуляции. Для всех значений две сгенерированные последовательности одинаковы.
Используйте comm.BarkerCode Системный объект и Barker Code Generator блок для генерации кодов Баркера для выполнения синхронизации. Коды штриха являются подмножествами псевдошумовых последовательностей. Они являются короткими кодами с длиной самое большее 13, которые являются боковыми телами с низкой корреляцией. Корреляционный боковой elobe является корреляцией кодового слова с измененной во времени версией самого себя.
Ортогональные коды используются для расширения, чтобы извлечь пользу из их совершенных корреляционных свойств. При использовании в многопользовательских системах расширенного спектра, где приемник идеально синхронизируется с передатчиком, операция сжатия идеальна.
| Код | Системный объект | Блок |
|---|---|---|
| Коды Адамара | comm.HadamardCode | Hadamard Code Generator |
| Коды OVSF | comm.OVSFCode | OVSF Code Generator |
| Коды Уолша | comm.WalshCode | Walsh Code Generator |
Библиотека блоков Comm Sinks содержит возможности для просмотра трех типов сигнальных графиков:
В следующей таблице перечислены блоки и графики, которые они генерируют.
| Имя блока | Графики |
|---|---|
| Eye Diagram Scope | Глазковая диаграмма сигнала |
| Constellation Diagram | Сигнальная схема и траектория сигнала |
Глазковая диаграмма является простым и удобным инструментом для исследования эффектов межсимвольной интерференции и других нарушений канала в цифровой передаче. Когда этот программный продукт создает глазковую диаграмму, он строит график принимаемого сигнала со временем на оси с фиксированным интервалом. В конце фиксированного интервала он оборачивается к началу оси времени. В результате схема состоит из многих перекрывающихся кривых. Одним из способов использования глазковой диаграммы является поиск места, где глаз наиболее широко открыт, и использование этой точки в качестве точки принятия решения при демодуляции демодулированного сигнала для восстановления цифрового сообщения.
Блок Eye Diagram Scope создает глазковые диаграммы. Этот блок обрабатывает сигналы в дискретном времени и периодически рисует линию, чтобы указать решение, согласно параметру маски.
Примеры появляются в View a Sinusoid и View a Moduled Signal.
Схема созвездия сигнала строит график значения сигнала в точках его принятия решения. В лучшем случае точки принятия решения должны быть в моменты, когда глаз глазковой диаграммы сигнала является наиболее широко открытым.
Блок Constellation Diagram производит сигнальное созвездие из сигналов дискретного времени. Пример появляется в View a Sinusoid.
Траектория сигнала является непрерывным графиком сигнала с течением времени. Траектория сигнала отличается от графика поля точек тем, что последние отображения указывают на траекторию сигнала с дискретными интервалами времени.
Блок Constellation Diagram производит траектории сигналов. Блок Constellation Diagram производит траектории сигналов, когда ShowTrajectory для свойства задано значение true. Траектория сигнала соединяет все точки входного сигнала, независимо от заданного коэффициента десятикратного уменьшения (Samples per symbol)
Следующая модель производит сигнальное созвездие и глазковую диаграмму от комплексного синусоидального сигнала. Поскольку временной интервал принятия решения является почти, но не точно, целым числом, кратным периоду синусоиды, глазковая диаграмма показывает дрейф с течением времени. Более конкретно, последующие следы в глазковой диаграмме и последующие точки в схеме рассеяния находятся рядом друг с другом, но не перекрываются.
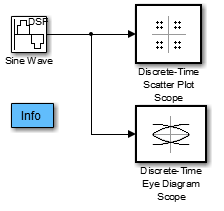
Чтобы открыть модель, введите doc_eyediagram в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:
Sine Wave, в библиотеке Sources DSP System Toolbox™ (не блок Sine Wave в библиотеке Simulink Sources)
Установите Frequency значение .502.
Установите Output complexity значение Complex.
Установите Sample time значение 1/16.
Constellation Diagram, в библиотеке Comm Sinks
На панели Constellation Properties установите Samples per symbol равным 16.
Eye Diagram Scope, в библиотеке Comm Sinks
На панели Plotting Properties установите Samples per symbol равным 16.
На панели Figure Properties установите Scope position равным figposition([42.5 55 35 35]);.
Соедините блоки как показано на предыдущем рисунке. В Simulate разделе установите Stop time равным 250. Раздел Simulate появляется на нескольких вкладках. Выполнение модели создает следующий график схемы рассеяния.
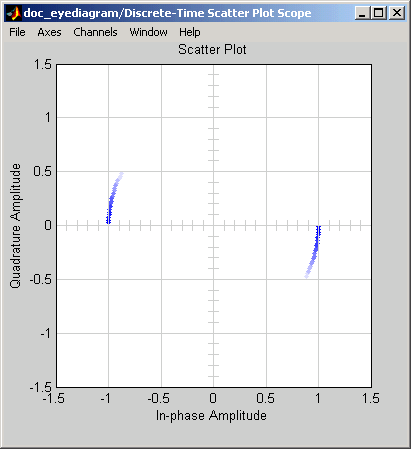
Точки графика поля точек лежат на окружности радиуса 1. Обратите внимание, что точки исчезают, когда время проходит. Это связано с тем, что флажок рядом с Color fading установлен под Rendering Properties, что заставляет возможности визуализировать точки более туго, чем больше времени проходит после построения графика. Если вы очистите это поле, вы увидите полный круг точек.
Блок «Схема созвездия» отображает круговую траекторию.
В глазковой диаграмме верхний набор трасс представляет действительную часть сигнала, а нижний набор трасс представляет воображаемую часть сигнала.
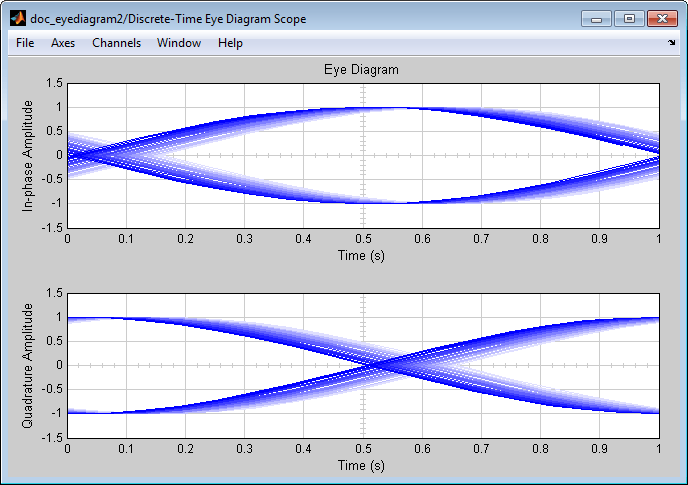
Этот многолучевой пример создает глазковую диаграмму, график поля точек и график траектории сигнала для модулированного сигнала. Он исследует графики один за другим в следующих разделах:
Следующая модель модулирует случайный сигнал, используя QPSK, фильтрует сигнал с фильтр приподнятого косинуса и создает глазковую диаграмму из фильтрованного сигнала.
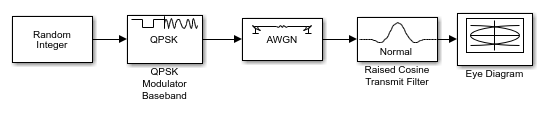
Чтобы открыть модель, введите doc_signaldisplays в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте следующие блоки:
Random Integer Generator, в поддиапазоне «Случайные источники данных» библиотеки Comm Sources
Установите M-ary number значение 4.
Установите Sample time значение 0.01.
QPSK Modulator Baseband, в PM в поддиапазоне Digital Baseband библиотеки Modulation Communications Toolbox с параметрами по умолчанию
AWGN Channel в библиотеке Channels Communications Toolbox со следующими изменениями в настройках параметра по умолчанию:
Установите Mode значение Signal-to-noise ratio (SNR).
Установите SNR (dB) значение 15.
Raised Cosine Transmit Filter, в библиотеке Comm Filters
Установите Filter shape значение Normal.
Установите Rolloff factor значение 0.5.
Установите Filter span in symbols значение 6.
Установите Output samples per symbol значение 8.
Установите Input processing значение Elements as channels (sample based).
Eye Diagram Scope, в библиотеке Comm Sinks
Установите Samples per symbol значение 8.
Установите Symbols per trace значение 3. Это задает количество символов, которые отображаются в каждой трассировке глазковой диаграммы. Трассировка является любой из отдельных линий в глазковой диаграмме.
Установите Traces displayed значение 3.
Установите New traces per display значение 1. Это задает количество новых трассировок, которые появляются при каждом обновлении схемы. Количество трассировок, которые остаются в схеме от одного обновления до следующего, Traces displayed минус New traces per display.
На панели Rendering Properties установите Markers равным + для указания точек, нанесенных на каждую выборку. Значение по умолчанию Markers является пустым, что указывает на отсутствие маркера.
На панели Figure Properties установите Eye diagram to display равным In-phase only.
Когда вы запускаете модель, Глазковая диаграмма отображает следующую схему. Точное изображение изменяется в зависимости от того, когда вы останавливаете или останавливаете симуляцию.
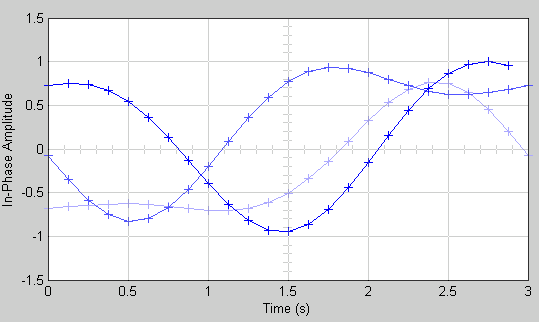
Отображаются три трассировки. Трассировки 2 и 3 замирают, потому что Color fading под Rendering Properties выбран. Это приводит к тому, что следы отображаются менее ярко, чем они старше. На этом рисунке трассировка 1 является самой последней, а трассировка 3 - самой старой. Потому что New traces per display установлено на 1, только трассировка 1 появляется впервые. Трассировки 2 и 3 также появляются на предыдущем отображении.
Потому что Symbols per trace установлено на 3каждая трассировка содержит три символа, и потому что Samples per trace задано значение 8каждый символ содержит восемь выборок. Обратите внимание, что трассировка 1 содержит 24 точки, что является продуктом Symbols per trace и Samples per symbol. Однако трассировки 2 и 3 содержат по 25 точек. Последняя точка трассировки 2, на правой границе возможностей, представляет собой ту же выборку, что и первая точка трассировки 1, на левой границе возможностей. Точно так же последняя точка в трассировке 3 представляет ту же выборку, что и первая точка в трассировке 2. Эти повторяющиеся точки указывают, где будут совпадать трассировки, если они отображались один за другим, как показано на следующем рисунке.
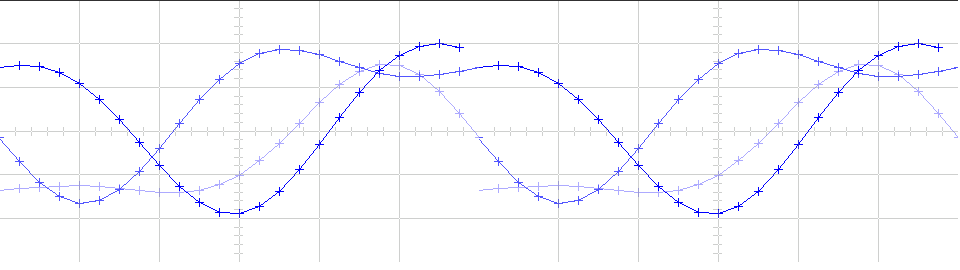
Можно просмотреть более реалистичную глазковую диаграмму, изменив значение Traces displayed на 40 и очистку поля Markers .
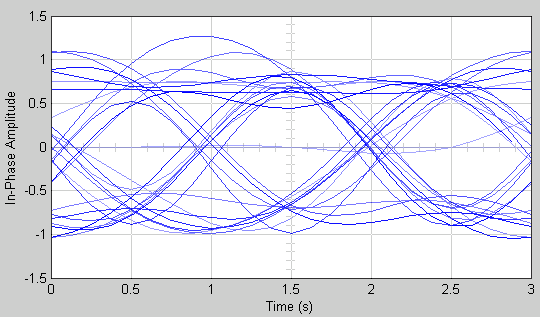
Когда параметр Offset установлен в 0, графическое изображение начинается в центре первого символа, так что открытая часть глазковой диаграммы находится в середине графика для большинства точек.
Следующая модель создает график поля точек того же сигнала, рассматриваемого в Глазковую диаграмму Модулированного Сигнала.

Чтобы создать модель, следуйте инструкциям в Глазковая Диаграмма of a Moduled Signal, но замените блок Глазковая диаграмма на следующий блок:
Constellation Diagram, в библиотеке Communications Toolbox/Comm Sinks
Установите Samples per symbol значение 2
Установите Offset значение 0. Это задает количество выборок, которые нужно пропустить перед построением графика первой точки.
Установите Symbols to display значение 40.
Когда вы запускаете симуляцию, блок Constellation Diagram отображает следующий график.
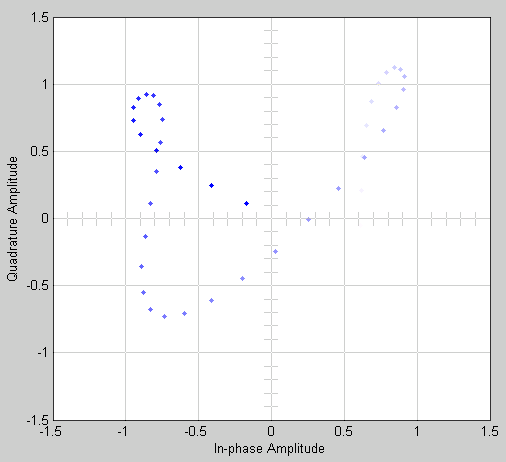
График отображает 30 точек. Поскольку Color fading под Rendering Properties выбран, точки отображаются менее ярко, чем они старше.
Следующая модель создает график траектории сигнала того же сигнала, рассматриваемого в Глазковая Диаграмма Модулированного Сигнала.
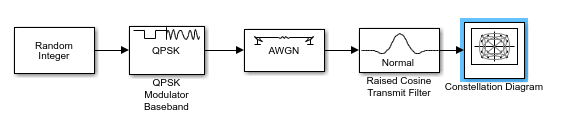
Чтобы создать модель, следуйте инструкциям в Глазковая Диаграмма of a Moduled Signal, но замените блок Глазковая диаграмма на следующий блок:
Constellation Diagram , в библиотеке Communications Toolbox/Comm Sinks
Установите Samples per symbol значение 8.
Установите Symbols to display значение 40. Это определяет количество символов, отображаемых в траектории сигнала. Отображаемое общее число точек является продуктом Samples per symbol и Symbols to display.
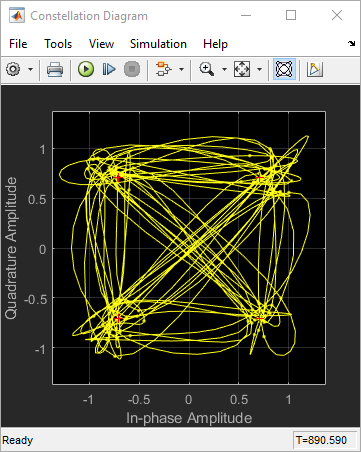
Когда вы запускаете модель, Схема Созвездия отображает траекторию, подобную следующей.
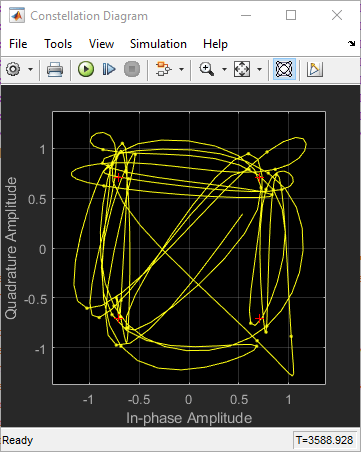
На графике отображается 40 символов. Поскольку Color fading под Rendering Properties выбран, символы отображаются менее ярко, чем старше.
Смотрите Сигнальное Созвездие Модулированного Сигнала, чтобы сравнить предыдущую сигнальную траекторию с графиком поля точек того же сигнала. Блок Созвездие Program соединяет точки, отображаемые блоком Constellation Diagram, чтобы отобразить траекторию сигнала.
Если вы увеличиваете Symbols to display до 100, модель производит сигнальную траекторию, подобную приведенной ниже. Общее число точек, отображаемых в любой момент, составляет 800, что является продуктом параметров Samples per symbol и Symbols to display.