Документация

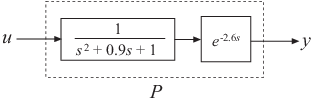
Создайте образец разомкнутого контура системы с выходом задержкой.

s = tf('s');
P = exp(-2.6*s)/(s^2+0.9*s+1);

P является передаточной функцией второго порядка (tf) объект с временной задержкой.

Вычислите приближение Паде первого порядка P.

Pnd1 = pade(P,1)

Pnd1 =
 
             -s + 0.7692
  ----------------------------------
  s^3 + 1.669 s^2 + 1.692 s + 0.7692
 
Continuous-time transfer function.

Эта команда заменяет все задержки в P с приближением первого порядка. Поэтому Pnd1 является передаточной функцией третьего порядка без задержек.

Сравните частотную характеристику исходной и приблизительной моделей, используя bodeplot.

h = bodeoptions;
h.PhaseMatching = 'on';
bodeplot(P,'-b',Pnd1,'-.r',{0.1,10},h)
legend('Exact delay','First-Order Pade','Location','SouthWest')

Величина P и Pnd1 точно соответствовать. Однако фаза Pnd1 отклоняется от фазы P за пределами примерно 1 рад/с.

Увеличьте приближение Padé, чтобы расширить частотную полосу, в котором фаза приближения хороша.

Pnd3 = pade(P,3);

Сравните частотную характеристику P, Pnd1 и Pnd3.

bodeplot(P,'-b',Pnd3,'-.r',Pnd1,':k',{0.1 10},h)
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','SouthWest')

Ошибка приближения фазы уменьшается при помощи приближения Паде третьего порядка.

Сравните отклики во временном интервале исходной и аппроксимированной систем, используя stepplot.

stepplot(P,'-b',Pnd3,'-.r',Pnd1,':k')
legend('Exact delay','Third-Order Pade','First-Order Pade',...
       'Location','Southeast')

Использование приближения Паде вводит неминимальный программный продукт фазы (эффект «неправильного пути») в начальном переходном процессе. Эффект довольно выражен в приближении первого порядка, которое значительно опускается ниже нуля перед изменением направления. Эффект уменьшается в приближении более высокого порядка, которая намного более близко соответствует точной реакции системы.