Использование InputDelay, OutputDelay, и ioDelay свойства, можно смоделировать простые процессы с задержками транспорта. Однако эти свойства не могут моделировать более сложные ситуации, такие как циклы обратной связи с задержками. В дополнение к InputDelay и OutputDelay свойства, пространство состояний (ss) модели имеют InternalDelay свойство. Это свойство позволяет моделировать взаимосвязь систем с входами, вывода или транспорта, включая циклы обратной связи с задержками. Можно использовать InternalDelay свойство для точной моделирования и анализа произвольных линейных систем с задержками. Внутренние задержки могут возникнуть из-за следующего:
Конкатенация моделей в пространстве состояний с входами и выхода.
Обратная передача задержанного сигнала.
Преобразование MIMO tf или zpk модели с задержками переноса в форму пространство состояний.
Используя внутренние задержки, вы можете сделать следующее:
За непрерывное время сгенерируйте свободные от аппроксимации симуляции времени и частоты, потому что задержки не должны быть заменены приближением Паде. За непрерывное время это позволяет более точно анализировать системы с длительными задержками.
В дискретном времени сохраните задержки отдельно от другой динамики системы, потому что задержки не заменяются полюсами в z = 0, что повышает эффективность временных и частотных симуляций для систем дискретного времени с длинными задержками.
Используйте большинство функций Control System Toolbox™.
Тестируйте расширенные стратегии управления для отложенных систем. Для примера можно реализовать и протестировать точную модель предиктора Смита. Смотрите пример Управление процессами с длинным мертвым временем: Предсказатель Смита.
Этот пример иллюстрирует, почему задержек ввода, выхода и транспорта недостаточно для моделирования всех типов задержек, которые могут возникнуть в динамических системах. Рассмотрим простой цикл обратной связи с задержкой 2 с.:
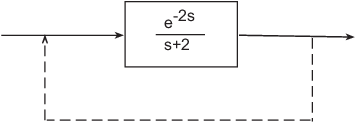
Передаточная функция с обратной связью
Срок задержки в числителе может быть представлен как выход задержка. Однако срок задержки в знаменателе не может. В порядок моделирования эффекта задержки на цикл обратной связи InternalDelay свойство необходимо для отслеживания внутренней связи между задержками и обычной динамикой.
Обычно вы не создаете модели пространства состояний с внутренними задержками непосредственно, задавая A, B, C и матрицы D вместе с набором внутренних задержек. Скорее такие модели возникают, когда вы соединяете модели с задержками. Нет никаких ограничений на то, сколько задержек связано и как модели связаны. Для примера создания внутренней задержки путем закрытия цикла обратной связи, смотрите Закрытие циклов обратной связи с временными задержками.
Когда вы работаете с моделями, имеющими внутренние задержки, будьте в курсе следующего поведения:
Когда соединение моделей приводит к внутренним задержкам, программное обеспечение возвращает ss модель независимо от взаимосвязанных типов модели. Это происходит потому, что только ss поддерживает внутренние задержки.
Программа полностью поддерживает циклы обратной связи. Вы можете обернуть цикл обратной связи вокруг любой системы с задержками.
При отображении A, B, C, и D матрицы, программное обеспечение устанавливает все задержки в нуль (создавая приближение Паде нулевого порядка). Это приближение происходит только для отображения, а не для вычислений с использованием модели.
Для некоторых систем установка задержек на нуль создает сингулярные алгебраические циклы, которые приводят к неправильным или плохо определенным приближениям с нулевой задержкой. Для этих систем:
Ввод sys возвращает только размеры для матриц системы с именем sys.
Ввод sys.A приводит к ошибке.
Ограниченное отображение и ошибка не подразумевают проблемы с моделью sys сам.
Объекты в пространстве состояний используют обобщенные уравнения в пространстве состояний, чтобы отслеживать внутренние задержки. Концептуально такие модели состоят из двух взаимосвязанных частей:
Модель H (s) обычного пространства состояний с дополненным набором вводов-выводов
Банк внутренних задержек.
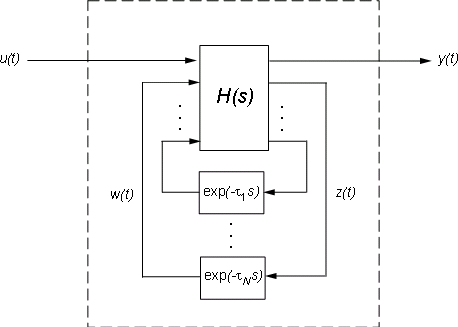
Соответствующие уравнения в пространстве состояний:
Вам не нужно беспокоиться об этом внутреннем представлении, чтобы использовать инструменты. Если, однако, вы хотите извлечь H или матрицы A, B1, B2, ... , вы можете использовать getDelayModelДля примера:
P = 5*exp(-3.4*s)/(s+1); C = 0.1 * (1 + 1/(5*s)); T = feedback(ss(P*C),1); [H,tau] = getDelayModel(T,'lft'); size(H)
Обратите внимание, что H является моделью с двумя входами, двумя выходами, в то время как T является SISO. Обратная операция (объединение H и tau для создания T) выполняется setDelayModel.
Следующие команды поддерживают внутренние задержки как для систем непрерывного, так и для дискретного времени:
Следующие команды поддерживают внутренние задержки как для систем непрерывного, так и для дискретного времени и имеют определенные ограничения:
allmargin, margin- Использует интерполяцию, поэтому эти команды являются только такими же точными, как и тонкость указанной сетки.
pole, zero- Возвращает полюса и нули системы с нулем всех задержек.
ssdata, get- Если у модели SS есть внутренние задержки, эти команды возвращают A, B, C, и D матрицы системы со всеми внутренними задержками, установленными на нуль. Использовать getDelayModel для доступа к представлению внутреннего пространства состояний моделей с внутренними задержками.
Следующие команды не поддерживают внутренние задержки:
Анализ временной области -initial и initialplot
Проект компенсатора -rlocus, lqg, lqry, lqrd, kalman, kalmd, lqgreg, lqgtrack, lqi, и augstate.
Чтобы использовать эти функции в системе с внутренними задержками, используйте pade для аппроксимации внутренних задержек. Смотрите Приближение задержки по времени.
[1] P. Gahinet and L.F. Shampine, «Software for Modeling and Analysis of линейные системы Delays», Proc. American Control Conf., Boston, 2004, pp. 5600-5605
[2] L.F. Shampine and P. Gahinet, Delay-дифференциально-алгебраические уравнения в теории управления, прикладная числовая математика, 56 (2006), стр. 574-588