Документация

Кубическая сплайн интерполяция сглаживающих данных

Предположим, что вы хотите интерполировать некоторые плавные данные, например, к

rng(6), x = (4*pi)*[0 1 rand(1,15)]; y = sin(x);

Можно использовать кубическую сплайн интерполяцию, полученную

cs = csapi(x,y);

и постройте график сплайна вместе с данными со следующим кодом:

fnplt(cs);
hold on
plot(x,y,'o')
legend('cubic spline','data')
hold off

Это создает рисунок, такую как следующая.

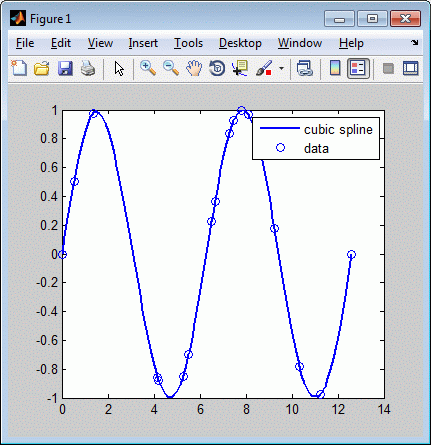
Это, точнее, кубическая сплайн интерполяция с граничными условиями и условиями отсутствия узла, что означает, что это уникальный кусочно-кубический полином с двумя непрерывными производными с пропусками во всех внутренних сайтах данных, кроме крайнего левого и крайнего правого. Это та же интерполяция, что и произведенная MATLAB^® spline команда, spline(x,y).

Периодические данные

Синусоидальная функция 2, - периодическая. Чтобы проверить, насколько хорошо ваша интерполяция работает по этому счету, вычислите, например, различие в значении его первой производной в двух конечных точках,

diff(fnval(fnder(cs),[0 4*pi]))
ans = -.0100

что не так хорошо. Если вы предпочитаете получить интерполяцию, первая и вторая производные которой находятся в двух конечных точках, 0 и 4*pi, match, использовать вместо этого команду csape который допускает спецификацию многих различных видов граничных условий, включая периодические граничные условия. Итак, используйте вместо этого

pcs = csape(x,y,'periodic');

для чего вы получаете

diff(fnval(fnder(pcs),[0 4*pi]))

Выход ans = 0 как различие концевых уклонов. Даже различие в конечных вторых производных небольшая:

diff(fnval(fnder(pcs,2),[0 4*pi]))

Выход ans = -4.6074e-015.

Другие граничные условия

Также могут быть обработаны и другие граничные условия. Для примера,

cs = csape(x,[3,y,-4],[1 2]);

обеспечивает кубическую сплайн интерполяцию с пропусками на и с ее наклоном на крайнем левом сайте данных, равным 3, и ее второй производной на крайнем правом сайте данных, равной -4.

Общий Сплайн интерполяция

Если вы хотите интерполировать в сайтах, отличных от пропусков и/или сплайнами, отличными от кубических сплайнов с простыми узлами, то вы используете spapi команда. В самой простой форме вы бы сказали sp = spapi(k,x,y); в котором первый аргумент, k, задает порядок интерполяции сплайна; это количество коэффициентов в каждой полиномиальной части, т.е. на 1 больше номинальной степени ее полиномиальных частей. Например, следующий рисунок показывает линейную, квадратичную и квартальную сплайн интерполяцию к вашим данным, полученную операторами

sp2 = spapi(2,x,y); fnplt(sp2,2), hold on
sp3 = spapi(3,x,y); fnplt(sp3,2,'k--'), 
sp5 = spapi(5,x,y); fnplt(sp5,2,'r-.'), plot(x,y,'o')
legend('linear','quadratic','quartic','data'), hold off

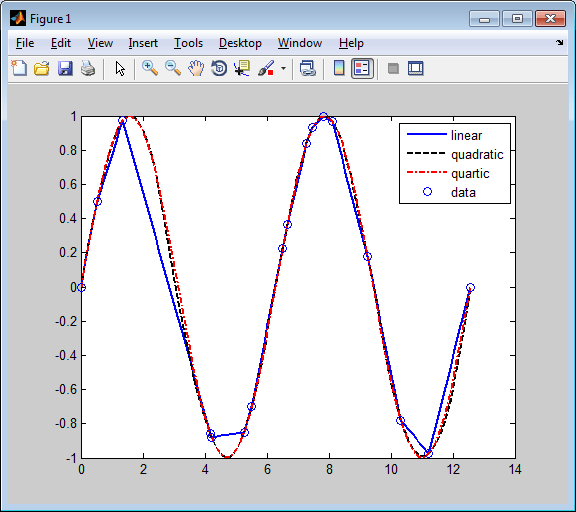
Даже кубическая сплайн интерполяция, полученная из spapi отличается от той, которая предоставляется csapi и spline. Чтобы подчеркнуть их различие, вычислите и постройте их вторые производные, следующим образом:

fnplt(fnder(spapi(4,x,y),2)), hold on,
fnplt(fnder(csapi(x,y),2),2,'k--'),plot(x,zeros(size(x)),'o')
legend('from spapi','from csapi','data sites'), hold off

Это даёт следующий график:

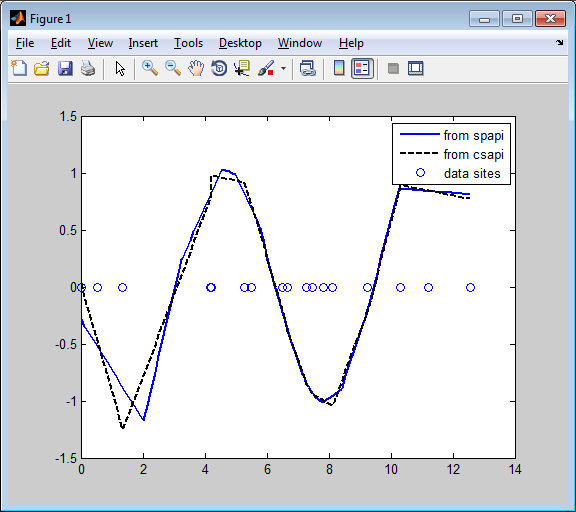
Поскольку вторая производная кубического сплайна является ломаной линией, с вершинами в пропусках сплайна, можно ясно увидеть, что csapi размещает пропуски на сайтах данных, в то время как spapi не делает.

Выбор узлов

Фактически можно явным образом задать, где должна иметь свои пропуски сплайн, используя команду sp = spapi(knots,x,y); в котором последовательность knots поставляет, определенным образом, пропуски, которые будут использоваться. Например, напоминая, что вы выбрали y чтобы быть sin(x), команду

ch = spapi(augknt(x,4,2),[x x],[y cos(x)]);

обеспечивает кубическую эрмитову интерполяцию в синусоидальную функцию, а именно кусочно-кубическую функцию, с пропусками на всех x(i)s, который соответствует функции синуса по значению и наклону на всех x(i)Это делает интерполяцию непрерывной с непрерывной первой производной, но, в целом, она имеет переходы через пропуски во второй производной. Как эта команда знает, какая часть массива значений данных  [y cos(x)] задает значения и какие склоны? Заметьте, что массив сайта данных здесь задан как [x x], т.е. каждый сайт данных появляется дважды. Также заметьте, что y(i) связана с первым вхождением x(i), и cos(x(i)) связана со вторым вхождением x(i). Значение данных, сопоставленное с первым внешним видом сайта данных, принято как значение функции; значение данных, сопоставленное со вторым внешним видом, принято за уклон. Если бы был третий внешний вид этого сайта данных, соответствующее значение данных было бы принято как второе производное значение, которое должно совпадать с этим сайтом. Смотрите построение и работа со сплайнами B-формы» для обсуждения команды augknt используется здесь для генерации соответствующей «последовательности узлов».

Сглаживание

Что, если данные зашумлены? Например, предположим, что заданные значения

noisy = y + .3*(rand(size(x))-.5);

Тогда вы можете предпочитать аппроксимировать вместо этого. Например, можно попробовать кубический сплайн сглаживания, полученный командой

scs = csaps(x,noisy);

и нанесено на график

fnplt(scs,2), hold on, plot(x,noisy,'o'),
legend('smoothing spline','noisy data'), hold off

Это создает рисунок:

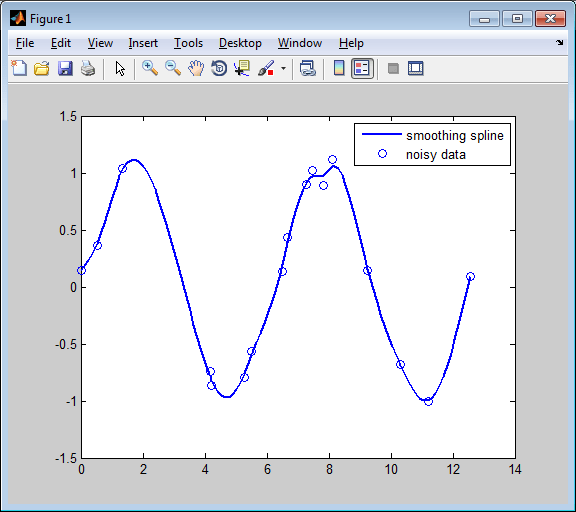
Если вам не нравится уровень сглаживания, выполняемый csaps(x,y), можно изменить его, задав параметр сглаживания, p, как необязательный третий аргумент. Выберите этот номер в диапазоне от 0 до 1. Как p изменяется от 0 до 1, сглаживающий сплайн изменяется, соответственно, с одного крайнего наименее квадратного прямолинейного приближения на данные, на другой крайний, «естественного» кубического сплайна интерполяции на данные. Начиная с csaps возвращает параметр сглаживания, фактически используемый в качестве дополнительного второго выхода, теперь можно экспериментировать следующим образом:

[scs,p] = csaps(x,noisy); fnplt(scs,2), hold on
fnplt(csaps(x,noisy,p/2),2,'k--'), 
fnplt(csaps(x,noisy,(1+p)/2),2,'r:'), plot(x,noisy,'o')
legend('smoothing spline','more smoothed','less smoothed',...
'noisy data'), hold off

Это создает следующую картину.

Иногда можно предпочитать просто получить самый гладкий кубический сплайн sp это в пределах заданного допуска tol данных в том смысле, что norm(noisy - fnval(sp,x))^2 <= tol. Вы создаете этот сплайн с помощью команды sp = spaps(x,noisy,tol) для вашего определенного допуска tol.

Наименьшие квадраты

Если вы предпочитаете аппроксимацию методом наименьших квадратов, можно получить её оператором sp = spap2(knots,k,x,y); в котором обе последовательности узлов knots и порядок k сплайн должен быть предусмотрен.

Популярный выбор для порядка - 4, и это дает вам кубический сплайн. Если вы не имеете ясного представления о том, как выбрать узлы, просто укажите количество полиномиальных частей, которые вы хотите использовать. Для примера,

sp = spap2(3,4,x,y); 

приводит кубический сплайн, состоящий из трех полиномиальных частей. Если получившаяся ошибка неравномерна, можно попробовать улучшить распределение узлов при помощи newknt следующим образом:

sp = spap2(newknt(sp),4,x,y);