Сравнение прогнозирующей эффективности после создания моделей с помощью приложения Econometric Modeler

В этом примере показано, как выбрать лаги для модели ARIMA путем сравнения значений AIC предполагаемых моделей с помощью приложения Econometric Modeler. Пример также показывает, как сравнить прогнозирующую эффективность нескольких моделей, которые имеют лучшие подгонки в выборке в командной строке. Набор данных Data_Airline.mat содержит ежемесячные подсчеты пассажиров авиакомпании.

Импорт данных в Econometric Modeler

В командной строке загрузите Data_Airline.mat набор данных.

load Data_Airline

Чтобы сравнить прогнозирующую эффективность позже, зарезервируйте последние два года данных в качестве выборки удержания.

fHorizon = 24;
HoldoutTable = DataTable((end - fHorizon + 1):end,:);
DataTable((end - fHorizon + 1):end,:) = [];

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Также откройте приложение из галереи Apps (см. Econometric Modeler).

Импортируйте DataTable в приложение:

На вкладке Econometric Modeler, в разделе Import, нажмите.
В Import Data окне в столбце Import? установите флажок для DataTable переменная.
Нажмите Import.

Переменная PSSG появляется на панели Time Series, его значение появляется на панели Preview, а график временных рядов появляется в Time Series Plot(PSSG) окне рисунка.

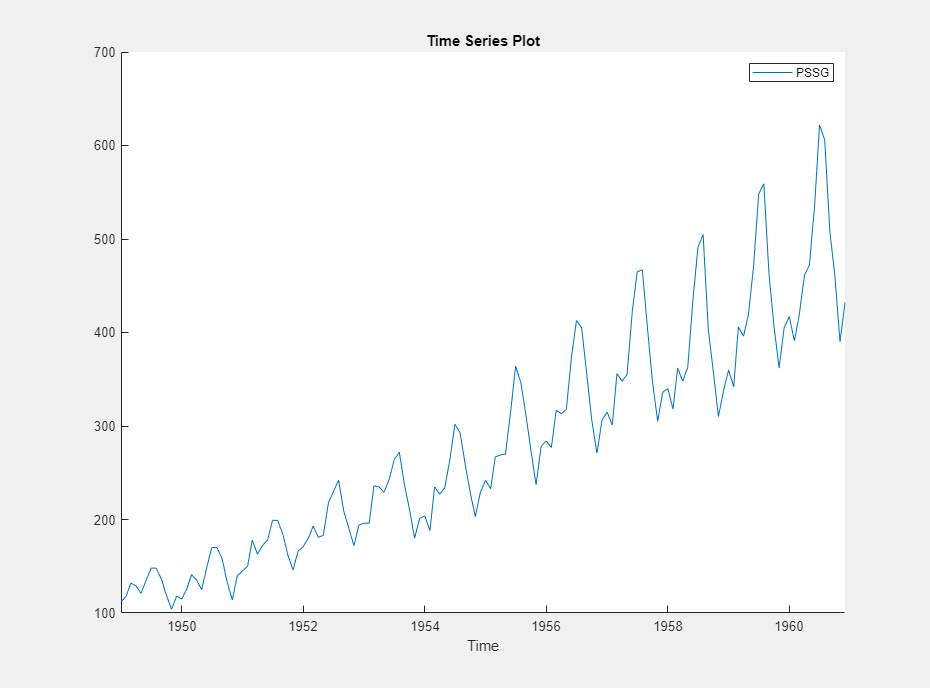
Серия демонстрирует сезонный тренд, последовательную корреляцию и возможный экспоненциальный рост. Интерактивный анализ последовательной корреляции см. в разделе Обнаружение последовательной корреляции с использованием приложения Econometric Modeler.

Удаление экспоненциального тренда

Адресовать экспоненциальный тренд, применив преобразование журнала к PSSG.

На панели Time Series выберите PSSG.
На вкладке Econometric Modeler, в разделе Transforms, нажмите Log.

Преобразованная переменная PSSGLog появляется на панели Time Series, его значение появляется на панели Preview, а график временных рядов появляется в Time Series Plot(PSSGLog) окне рисунка.

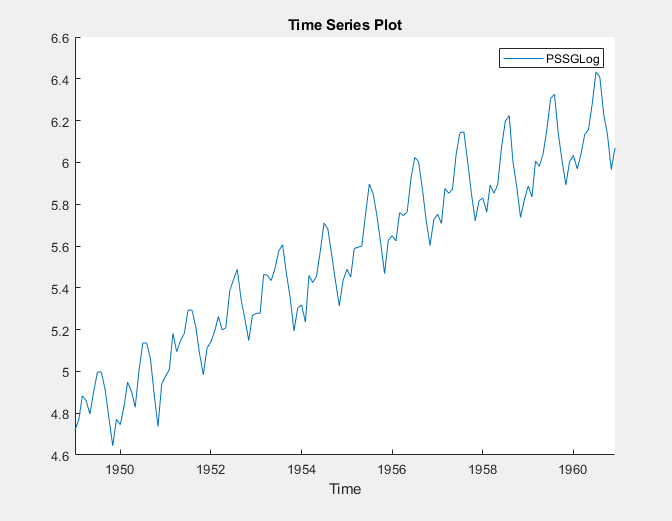
Экспоненциальный рост, по-видимому, удаляется из ряда.

Сравнение моделей в выборке

Box, Jenkins и Reinsel предлагают модель SARIMA (0,1,1) × (_0,1,1) 12 без константы для PSSGLog [1] (для получения дополнительной информации см. «Оценка мультипликативной модели ARIMA с использованием приложения Econometric Modeler»). Однако рассмотрим все комбинации ежемесячных моделей SARIMA, которые включают до двух сезонных и несезонных лагов MA. В частности, повторите следующие шаги для каждой из девяти моделей вида SARIMA (0,1, q) × (0,1, _q 12) 12, где q ∈ {0, 1, 2} и q ₁₂ ∈ {0, 1, 2}.

Для первой итерации:
1. Предположим q = q ₁₂ = 0.
2. С PSSGLog на панели Time Series щелкните вкладку Econometric Modeler. В Models разделе щелкните стреле, чтобы отобразить коллекцию моделей.
3. В галерее моделей, в ARMA/ARIMA Models разделе, нажмите SARIMA.
4. В диалоговом окне SARIMA Model Parameters на вкладке Lag Order:
  - Nonseasonal раздел
    Установите Degrees of Integration значение 1.
    Установите Moving Average Order значение 0.
    Снимите флажок Include Constant Term.
  - Seasonal раздел
    Установите Period значение 12 для указания ежемесячных данных.
    Установите Moving Average Order значение 0.
    Установите флажок Include Seasonal Difference.
5. Нажмите Estimate.
Переименуйте новую переменную модели.
1. На панели Models дважды щелкните новую переменную модели, чтобы выбрать ее имя.
2. Введите SARIMA01 q_{x01 <reservedrangesplaceholder0>}. Для примера, когда q = _q12 = 0, переименуйте переменную в SARIMA010x010.
В Сводные данные Model (SARIMA01 q_{x01 <reservedrangesplaceholder0>}), в таблице Goodness of Fit отметьте значение AIC. Для примера, для переменной модели SARIMA010x010, AIC на этом рисунке.
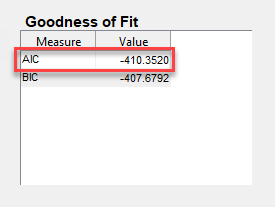
Для следующей итерации выберите значения q и q ₁₂. Для примера q = 0 и _q 12 = 1 для второй итерации.
На панели Models щелкните правой кнопкой мыши SARIMA01 q_{x01 <reservedrangesplaceholder0>}. В контекстном меню выберите Modify, чтобы открыть диалоговое окно SARIMA Model Parameters с текущими настройками для выбранной модели.
В диалоговом окне SARIMA Model Parameters:
1. В Nonseasonal разделе установите Moving Average Order равным q.
2. В Seasonal разделе установите Moving Average Order равным _q12.
3. Нажмите Estimate.

После выполнения шагов панель Models содержит девять предполагаемых моделей с именем SARIMA010x010 через SARIMA012x012.

Результирующие значения AIC приведены в этой таблице.

Модель	Имя переменной	AIC
SARIMA (0,1,0) × (_0,1,0) 12	`SARIMA010x010`	-410.3520
SARIMA (0,1,0) × (_0,1,1) 12	`SARIMA010x011`	-443.0009
SARIMA (0,1,0) × (_0,1,2) 12	`SARIMA010x012`	-441.0010
SARIMA (0,1,1) × (_0,1,0) 12	`SARIMA011x010`	-422.8680
SARIMA (0,1,1) × (_0,1,1) 12	`SARIMA011x011`	-452.0039
SARIMA (0,1,1) × (_0,1,2) 12	`SARIMA011x012`	-450.0605
SARIMA (0,1,2) × (_0,1,0) 12	`SARIMA012x010`	-420.9760
SARIMA (0,1,2) × (_0,1,1) 12	`SARIMA012x011`	-450.0087
SARIMA (0,1,2) × (_0,1,2) 12	`SARIMA012x012`	-448.0650

Тремя моделями, дающими наименьшие три значения AIC, являются SARIMA (0,1,1) × (_0,1,1) 12, SARIMA (0,1,1) × _(0,1,2) 12 и SARIMA (0,1,2₎ × (0,1,1) 12. Эти модели имеют лучшую парсимонистскую подгонку в выборке.

Экспорт лучших моделей в рабочую область

Экспортируйте модели с лучшими подгонками в выборке.

На вкладке Econometric Modeler, в разделе Export, нажмите.
В диалоговом окне Export Variables в столбце Models установите флажок Select для SARIMA011x011, SARIMA011x012, и SARIMA012x011. Снимите флажок для любых других выбранных моделей.
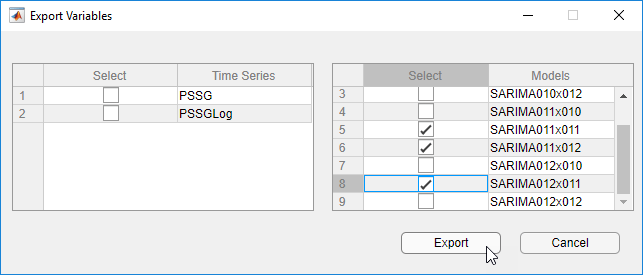
Нажмите Export.

The arima моделировать объекты SARIMA011x011, SARIMA011x012, и SARIMA012x011 появится в MATLAB^® Рабочая область.

Оценка прогнозов

В командной строке оцените прогнозы на два года вперед для каждой модели.

f5 = forecast(SARIMA_PSSGLog5,fHorizon);
f6 = forecast(SARIMA_PSSGLog6,fHorizon);
f8 = forecast(SARIMA_PSSGLog8,fHorizon);

f5, f6, и f8 являются векторами 24 на 1, содержащими прогнозы.

Сравнение среднеквадратических ошибок предсказания

Оцените среднюю квадратную ошибку предсказания (PMSE) для каждого из векторов прогноза.

logPSSGHO = log(HoldoutTable.Variables);
pmse5 = mean((logPSSGHO - f5).^2);
pmse6 = mean((logPSSGHO - f6).^2);
pmse8 = mean((logPSSGHO - f8).^2);

Идентифицируйте модель, получая самый низкий PMSE.

[~,bestIdx] = min([pmse5 pmse6 pmse8],[],2)

Модель SARIMA (0,1,1) × (_0,1,1) 12 выполняет лучшую in-sample и out-of-sample.

Ссылки

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Анализ временных рядов: прогнозирование и управление. 3-й эд. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1994.

Документация