forecast
Класс: regARIMA
Прогнозные отклики регрессионной модели с ошибками ARIMA
Синтаксис
[Y,YMSE]
= forecast(Mdl,numperiods)
[Y,YMSE,U]
= forecast(Mdl,numperiods)
[Y,YMSE,U]
= forecast(Mdl,numperiods,Name,Value)
Описание
[ прогнозы откликов (Y,YMSE]
= forecast(Mdl,numperiods)Y) для регрессионной модели с ошибками временных рядов ARIMA и генерирует соответствующие средние квадратные ошибки (YMSE).
[ дополнительно прогнозирует безусловные нарушения порядка для регрессионной модели с ошибками ARIMA.Y,YMSE,U]
= forecast(Mdl,numperiods)
[ прогнозы с дополнительными опциями, заданными одним или несколькими Y,YMSE,U]
= forecast(Mdl,numperiods,Name,Value)Name,Value аргументы в виде пар.
Входные параметры
Выходные аргументы
Примеры
Прогнозные отклики регрессионной модели с ошибками ARIMA
Прогнозные ответы из следующей регрессионной модели с ошибками ARMA (2,1) в 30-периодическом горизонте :
где является Гауссовым с отклонением 0,1.
Задайте модель. Симулируйте ответы от модели и двух рядов предикторов.
Mdl0 = regARIMA('Intercept',0,'AR',{0.5 -0.8},... 'MA',-0.5,'Beta',[0.1 -0.2],'Variance',0.1); rng(1); % For reproducibility X = randn(130,2); y = simulate(Mdl0,130,'X',X);
Подгонка модели к первым 100 наблюдениям и резервирование остальных 30 наблюдений для оценки эффективности прогноза.
Mdl = regARIMA('ARLags',1:2); EstMdl = estimate(Mdl,y(1:100),'X',X(1:100,:));
Regression with ARMA(2,0) Error Model (Gaussian Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Intercept 0.004358 0.021314 0.20446 0.83799
AR{1} 0.36833 0.067103 5.4891 4.0408e-08
AR{2} -0.75063 0.090865 -8.2609 1.4453e-16
Beta(1) 0.076398 0.023008 3.3205 0.00089863
Beta(2) -0.1396 0.023298 -5.9919 2.0741e-09
Variance 0.079876 0.01342 5.9522 2.6453e-09
EstMdl является новым regARIMA модель, содержащая оценки. Оценки близки к их истинным значениям.
Использование EstMdl для прогнозирования 30-периодического горизонта. Визуально сравните прогнозы с данными отключения с помощью графика.
[yF,yMSE] = forecast(EstMdl,30,'Y0',y(1:100),... 'X0',X(1:100,:),'XF',X(101:end,:)); figure plot(y,'Color',[.7,.7,.7]); hold on plot(101:130,yF,'b','LineWidth',2); plot(101:130,yF+1.96*sqrt(yMSE),'r:',... 'LineWidth',2); plot(101:130,yF-1.96*sqrt(yMSE),'r:','LineWidth',2); h = gca; ph = patch([repmat(101,1,2) repmat(130,1,2)],... [h.YLim fliplr(h.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend('Observed','Forecast',... '95% Forecast Interval','Location','Best'); title(['30-Period Forecasts and Approximate 95% '... 'Forecast Intervals']) axis tight hold off
Многие наблюдения в выборке holdout падают за 95% -ные интервалы прогноза. Для этого существуют две причины:
Предикторы генерируются случайным образом в этом примере.
estimateрассматривает предикторы как фиксированные. 95% интервалов прогноза на основе оценок изestimateне учитывайте изменчивость в предикторах.По вероятности сдвига период оценки кажется менее волатильным, чем период прогноза.
estimateиспользует менее изменчивые данные периода оценки для оценки параметров. Поэтому прогнозные интервалы, основанные на оценках, не должны охватывать наблюдения, которые имеют базовый инновационный процесс с большей изменчивостью.
Прогноз ВВП с использованием регрессионой модели с ошибками ARMA
Прогноз стационарный, журнал ВВП с использованием регрессионой модели с ошибками ARMA (1,1), включая ИПЦ в качестве предиктора .
Загрузите набор макроэкономических данных США и предварительно обработайте данные.
load Data_USEconModel; logGDP = log(DataTable.GDP); dlogGDP = diff(logGDP); % For stationarity dCPI = diff(DataTable.CPIAUCSL); % For stationarity numObs = length(dlogGDP); gdp = dlogGDP(1:end-15); % Estimation sample cpi = dCPI(1:end-15); T = length(gdp); % Effective sample size frstHzn = T+1:numObs; % Forecast horizon hoCPI = dCPI(frstHzn); % Holdout sample dts = dates(2:end); % Date nummbers
Подбор регрессионной модели с ошибками ARMA (1,1 ).
Mdl = regARIMA('ARLags',1,'MALags',1); EstMdl = estimate(Mdl,gdp,'X',cpi);
Regression with ARMA(1,1) Error Model (Gaussian Distribution):
Value StandardError TStatistic PValue
__________ _____________ __________ __________
Intercept 0.014793 0.0016289 9.0818 1.0684e-19
AR{1} 0.57601 0.10009 5.7548 8.6754e-09
MA{1} -0.15258 0.11978 -1.2738 0.20272
Beta(1) 0.0028972 0.0013989 2.071 0.038355
Variance 9.5734e-05 6.5562e-06 14.602 2.723e-48
Прогнозируйте темпы ВВП на 15-квартальном горизонте. Используйте выборку оценки в качестве предварительной выборки для прогноза.
[gdpF,gdpMSE] = forecast(EstMdl,15,'Y0',gdp,... 'X0',cpi,'XF',hoCPI);
Постройте график прогнозов и 95% интервалов прогноза.
figure h1 = plot(dts(end-65:end),dlogGDP(end-65:end),... 'Color',[.7,.7,.7]); datetick hold on h2 = plot(dts(frstHzn),gdpF,'b','LineWidth',2); h3 = plot(dts(frstHzn),gdpF+1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); plot(dts(frstHzn),gdpF-1.96*sqrt(gdpMSE),'r:','LineWidth',2); ha = gca; title(['{\bf Forecasts and Approximate 95% }'... '{\bf Forecast Intervals for GDP rate}']); ph = patch([repmat(dts(frstHzn(1)),1,2) repmat(dts(frstHzn(end)),1,2)],... [ha.YLim fliplr(ha.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend([h1 h2 h3],{'Observed GDP rate','Forecasted GDP rate ',... '95% Forecast Interval'},'Location','Best','AutoUpdate','off'); axis tight hold off
Прогноз с использованием регрессионной модели с ошибками ARIMA и известной точкой пересечения
Прогнозируйте корневой нестационарный, логарифмический ВВП с использованием регрессионой модели с ошибками ARIMA (1,1,1), включая ИПЦ в качестве предиктора и известный перехват .
Загрузите набор макроэкономических данных США и предварительно обработайте данные.
load Data_USEconModel; numObs = length(DataTable.GDP); logGDP = log(DataTable.GDP(1:end-15)); cpi = DataTable.CPIAUCSL(1:end-15); T = length(logGDP); % Effective sample size frstHzn = T+1:numObs; % Forecast horizon hoCPI = DataTable.CPIAUCSL(frstHzn); % Holdout sample
Задайте модель для периода оценки.
Mdl = regARIMA('ARLags',1,'MALags',1,'D',1);
Точка пересечения не идентифицируется в модели с интегрированными ошибками, поэтому исправьте его значение перед оценкой. Один из способов сделать это - оценить точку пересечения с помощью простой линейной регрессии.
Reg4Int = [ones(T,1), cpi]\logGDP; intercept = Reg4Int(1);
Рассмотрите выполнение анализа чувствительности при помощи сетки точек пересечения.
Установите точку пересечения и подгоните регрессионую модель с ошибками ARIMA (1,1,1 ).
Mdl.Intercept = intercept; EstMdl = estimate(Mdl,logGDP,'X',cpi,... 'Display','off')
EstMdl =
regARIMA with properties:
Description: "ARIMA(1,1,1) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: 5.80142
Beta: [0.00396706]
P: 2
D: 1
Q: 1
AR: {0.922709} at lag [1]
SAR: {}
MA: {-0.387844} at lag [1]
SMA: {}
Variance: 0.000108943
Regression with ARIMA(1,1,1) Error Model (Gaussian Distribution)
Прогнозируйте ВВП на 15-квартальном горизонте. Используйте выборку оценки в качестве предварительной выборки для прогноза.
[gdpF,gdpMSE] = forecast(EstMdl,15,'Y0',logGDP,... 'X0',cpi,'XF',hoCPI);
Постройте график прогнозов и 95% интервалов прогноза.
figure h1 = plot(dates(end-65:end),log(DataTable.GDP(end-65:end)),... 'Color',[.7,.7,.7]); datetick hold on h2 = plot(dates(frstHzn),gdpF,'b','LineWidth',2); h3 = plot(dates(frstHzn),gdpF+1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); plot(dates(frstHzn),gdpF-1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); ha = gca; title(['{\bf Forecasts and Approximate 95% }'... '{\bf Forecast Intervals for log GDP}']); ph = patch([repmat(dates(frstHzn(1)),1,2) repmat(dates(frstHzn(end)),1,2)],... [ha.YLim fliplr(ha.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend([h1 h2 h3],{'Observed GDP','Forecasted GDP',... '95% Forecast Interval'},'Location','Best','AutoUpdate','off'); axis tight hold off
Безусловные нарушения порядка, , являются нестационарными, поэтому ширина прогнозируемых интервалов увеличивается со временем.
Подробнее о
Временные Основы разделы для прогнозирования
Time base partitions for forecasting являются двумя несвязанными, смежными интервалами временной основы; каждый интервал содержит данные временных рядов для прогнозирования динамической модели. forecast period (горизонт прогноза) является numperiods разбиение длины в конце временной основы, в течение которой forecast генерирует прогнозы Y от динамической модели Mdl. Это presample period - весь раздел, возникший до периода прогноза. forecast может потребовать наблюдаемых реакций Y0, данные регрессии X0, безусловные нарушения порядка U0, или инновации E0 в периоде предварительного образца для инициализации динамической модели для прогнозирования. Структура модели определяет типы и объемы необходимых предварительных наблюдений.
Общей практикой является подгонка динамической модели к фрагменту набора данных, а затем подтверждение предсказуемости модели путем сравнения ее прогнозов с наблюдаемыми ответами. Во время прогноза период предварительного образца содержит данные, к которым подходит модель, а период прогноза содержит выборку удержания для валидации. Предположим, что yt является наблюдаемой последовательностью откликов; <reservedrangesplaceholder9> 1, t, <reservedrangesplaceholder7> 2, t, и <reservedrangesplaceholder5> 3, t наблюдаются внешний ряд; и time t = 1,..., T. Рассмотрите прогнозирование ответов из динамической модели y t, содержащей регрессионый компонент numperiods = K периоды. Предположим, что динамическая модель соответствует данным в интервале [1, T - K] (для получения дополнительной информации см. estimate). Этот рисунок показывает разделы основы времени для прогнозирования.
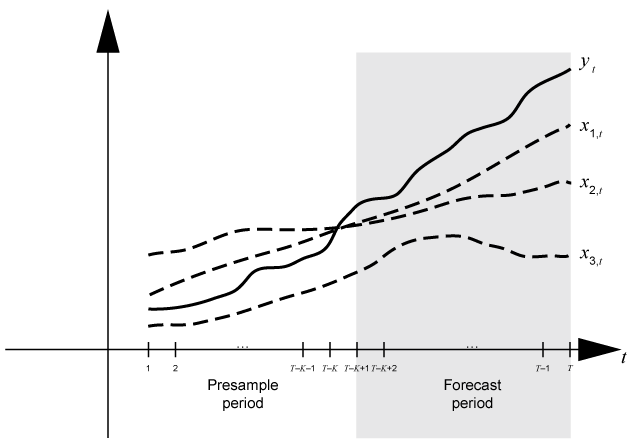
Для примера, чтобы сгенерировать прогнозы Y из регрессионной модели с AR (2) ошибками ,forecast требует предварительной выборки безусловных нарушений порядка U0 и будущие данные предиктора XF.
forecastвыводит безусловные нарушения порядка, учитывая достаточно легко доступные ответы presample и данные предиктора. Чтобы инициализировать модель ошибки AR (2),Y0= иX0= .К модели,
forecastтребует будущих экзогенных данныхXF= .
Этот рисунок показывает массивы необходимых наблюдений для общего случая с соответствующими входными и выходными аргументами.
Алгоритмы
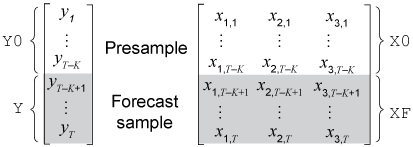
forecastвычисляет прогнозируемые MSE отклика,YMSE, путем обработки матриц данных предиктора (X0иXF) как нестохастический и статистически независимый от модельных инноваций. ПоэтомуYMSEотражает отклонение, связанную с безусловными нарушениями порядка только модели ошибки ARIMA.forecastиспользуетY0иX0для выводаU0. Поэтому, если вы задаетеU0,forecastигнорируетY0иX0.
Ссылки
[1] Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Анализ временных рядов: прогнозирование и управление. 3-й эд. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1994.
[2] Davidson, R., and J. G. MacKinnon. Эконометрическая теория и методы. Оксфорд, Великобритания: Oxford University Press, 2004.
[3] Enders, W. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.
[4] Гамильтон, Дж. Д. Анализ временных рядов. Princeton, NJ: Princeton University Press, 1994.
[5] Pankratz, A. Прогнозирование с динамическими регрессиоными моделями. John Wiley & Sons, Inc., 1991.
[6] Tsay, R.S. Analysis of Financial Time Series. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc., 2005.