До сих пор не разработано более формальное определение « выражения» и ее применения. Во многих ситуациях, когда денежный поток доступен, факторы дисконтирования денежных потоков могут быть не сразу очевидны. В других случаях релевантным часто является спред, различие между кривыми (также известная как терминология спреда).
Все эти расчеты требуют одного основного ингредиента, пятна Казначейства, par-доходности или прямой кривой. Как правило, генерация этих кривых начинается с ряда текущих и выбранных неработающих проблем в качестве входов.
MATLAB® программное обеспечение использует эти облигации для поиска спот-ставок по одному с самого короткого срока и далее, используя методы bootstrap. Все денежные потоки используются для построения спотовой кривой, и ставки между сроками (для этих купонов) интерполируются линейно.
Для рисунка того, как это работает, наблюдайте использование zbtyield (или эквивалентно zbtprice) по портфелю из шести казначейских векселей и облигаций.
Счета | Дата погашения | Текущее выражение |
|---|---|---|
3 месяца | 4/17/03 | 1.15 |
6 месяцев | 7/17/03 | 1.18 |
| Ноты/облигации | Купон | Дата погашения | Текущее выражение |
|---|---|---|---|
2 года | 1.750 | 12/31/04 | 1.68 |
5 лет | 3.000 | 11/15/07 | 2.97 |
10 лет | 4.000 | 11/15/12 | 4.01 |
30 лет | 5.375 | 2/15/31 | 4.92 |
Можно задать цены или выражений к облигациям выше, чтобы вывести спотовую кривую. Функция zbtyield принимает выражения (точное выражение).
Для продолжения сначала соберите вышеуказанную таблицу в переменную с именем Bonds. В первом столбце указаны сроки погашения, во втором - купоны, а в третьем - номиналы или лицевые значения облигаций. (Обратите внимание, что счета имеют нулевые купоны.)
Bonds = [datenum('04/17/2003') 0 100; datenum('07/17/2003') 0 100; datenum('12/31/2004') 0.0175 100; datenum('11/15/2007') 0.03 100; datenum('11/15/2012') 0.04 100; datenum('02/15/2031') 0.05375 100];
Затем задайте соответствующие выражения.
Yields = [0.0115;
0.0118;
0.0168;
0.0297;
0.0401;
0.0492];
Теперь вы готовы вычислить спотовую кривую для каждого из этих шести сроков. Кривая пятна основана на дате расчета 17 января 2003 года.
Settle = datenum('17-Jan-2003');
[ZeroRates, CurveDates] = zbtyield(Bonds, Yields, Settle)
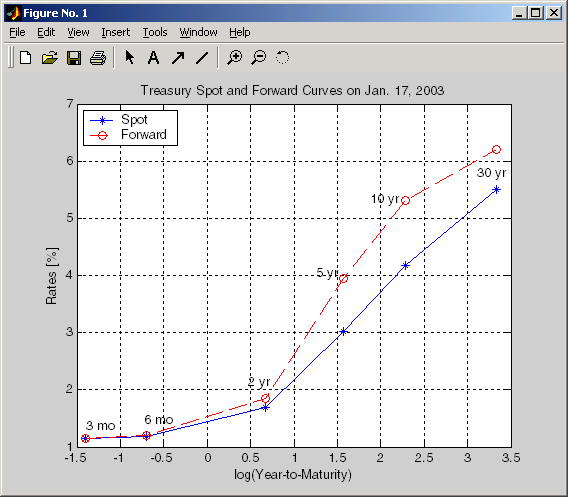
Это поможет вам получить спотовую кривую казначейства на день.
Можно вычислить прямую кривую из этой кривой пятна с zero2fwd.
[ForwardRates, CurveDates] = zero2fwd(ZeroRates, CurveDates, ... Settle)
Здесь понятие форвардных ставок относится к ставкам между указанными выше датами погашения, а не к определенному периоду (форвардные трехмесячные ставки для примера).
Вычисление спреда между конкретными фиксированными форвардными периодами (такими как спред Казначейство-Евродоллар) требует дополнительного шага. Интерполируйте нулевые ставки (или нулевые цены, вместо этого) для соответствующих сроков в датах интервала. Затем используйте интерполированные нулевые ставки, чтобы вывести форвардные ставки, и, таким образом, распределение сегментов прямой кривой Eurodollar по сравнению с соответствующими форвардными сегментами из казначейских векселей.
Кроме того, разнообразие функций кривой (включая zero2fwd) помогает стандартизировать такие расчеты. Например, путем создания обеих ставок, котируемых с ежеквартальным компаундированием и на фактической/360 базису, полученная структура спреда полностью сопоставима. Это позволяет избежать небольшого несоответствия, которое возникает при прямом сравнении выражения казначейского векселя с квартальными форвардными ставками, подразумеваемыми фьючерсами на Eurodollar.
При введении большего количества связей при построении кривых шум может стать фактором и может потребоваться некоторое «сглаживание» (со сплайнами, для примера); это помогает получить более плавную прямую кривую.
Следующие спотовые и форвардные кривые построены из 67 казначейских облигаций. Установленная и начальная кривая пятна (нижний правый рисунок) показывает сопоставимую стабильность. Прямая кривая (верхний левый рисунок) содержит значительный шум и показывает невероятную структуру прямой скорости. Шум не обязательно плох; он мог бы открыть торговые возможности для применения относительного подхода. Тем не менее, более сбалансированный подход желателен, когда загрузочная прямая кривая колеблется так много и содержит отрицательную скорость до -10% (не показана на графике, потому что она вне пределов).
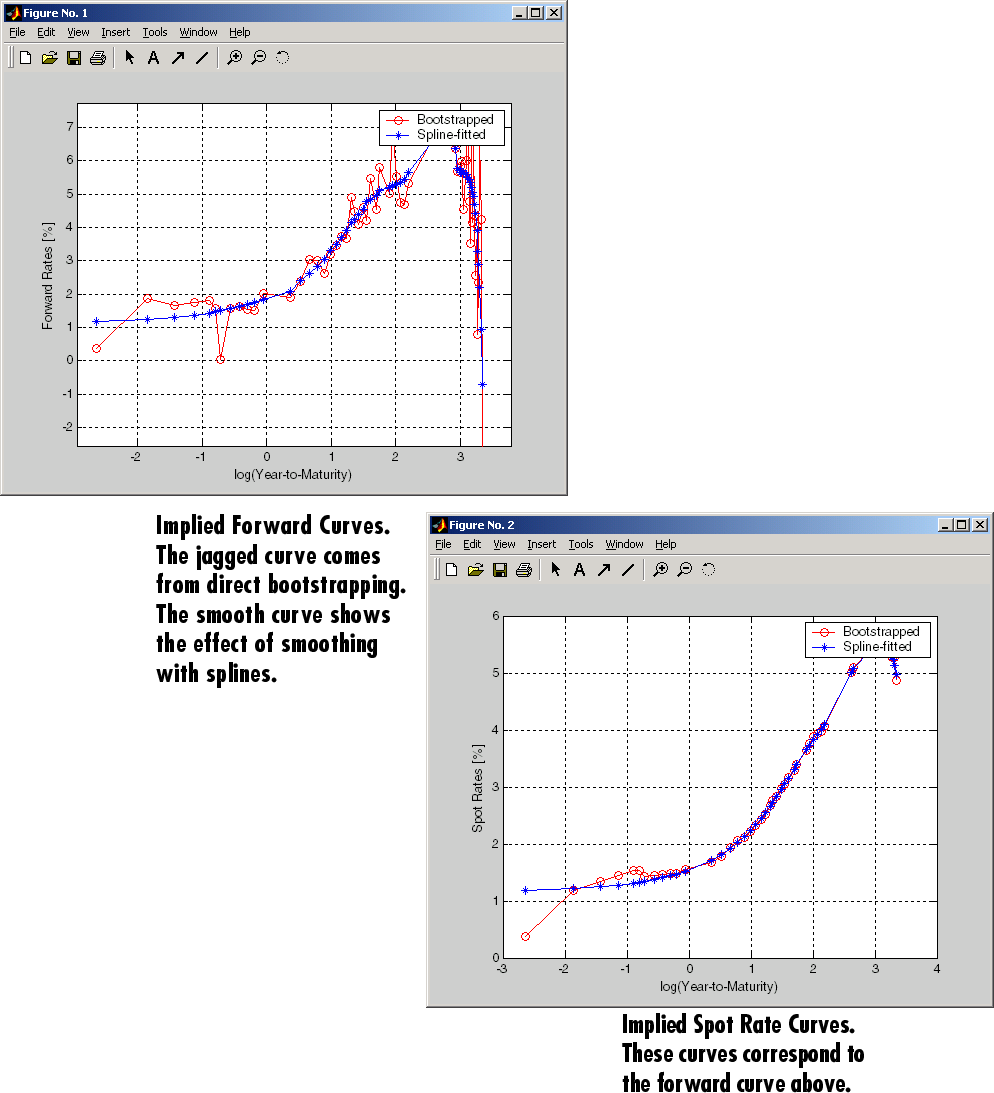
Этот пример использует termfit, функция , взятая в качестве примера, от программного обеспечения Financial Toolbox™, которая также требует использования программного обеспечения Curve Fitting Toolbox™.