Программное обеспечение Fuzzy Logic Toolbox™ поддерживает два типа систем нечеткого вывода:
Системы Мамдани
Системы Sugeno
| Система нечеткого вывода | Преимущества |
|---|---|
| Mamdani |
|
| Sugeno |
|
Нечеткий вывод Мамдани был впервые введен как метод создания системы управления путем синтеза набора лингвистических правил управления, полученных от опытных операторов человека [1]. В системе Мамдани выходы каждого правила являются нечетким множеством.
Поскольку системы Mamdani имеют более интуитивно понятные и более легкие для понимания основы правил, они хорошо подходят для экспертных системных приложений, где правила создаются из экспертных знаний человека, таких как медицинская диагностика.
Процесс вывода системы Мамдани описан в процессе нечеткого вывода и результирует на следующем рисунке.
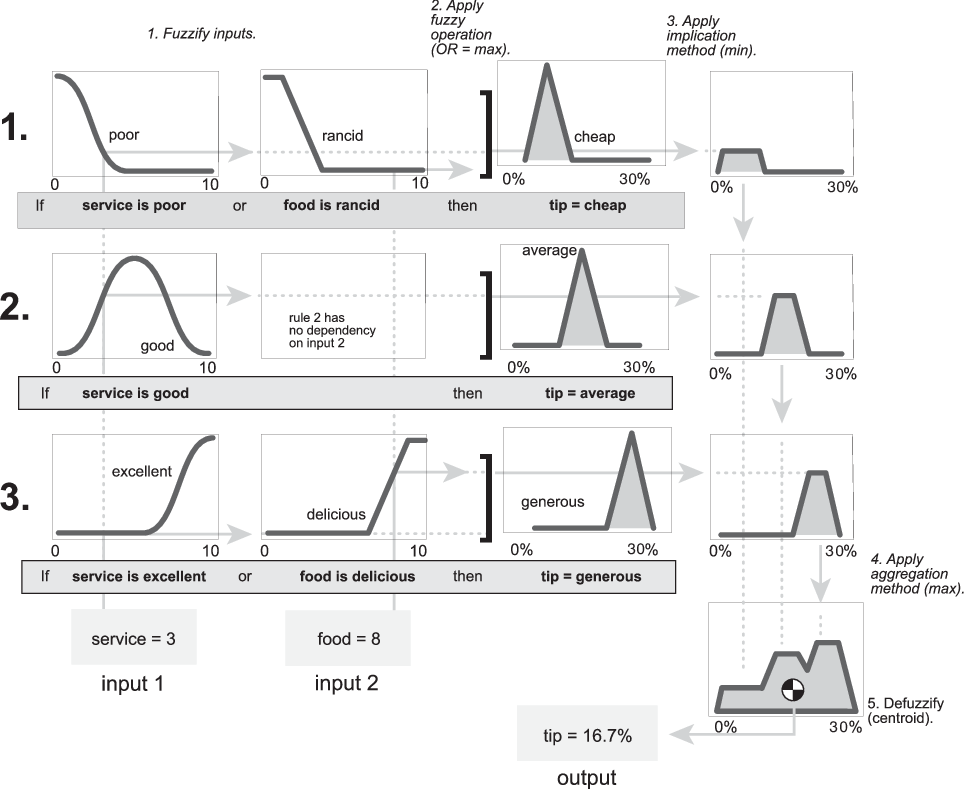
Выход каждого правила является нечетким множеством, полученным из функции принадлежности к выходу и импликационного метода FIS. Эти выходные нечеткие наборы объединяются в один нечеткий набор с помощью метода агрегации FIS. Затем, чтобы вычислить окончательное четкое выходное значение, объединенный выходной нечеткий набор дефузифицируют, используя один из методов, описанных в методах дефаззификации.
Sugeno нечеткий вывод, также упоминается как Takagi-Sugeno-Kang нечеткий вывод, использует синглтонные выходные функции принадлежности, которые являются либо постоянными, либо линейной функцией от входных значений. Процесс дефаззификации для системы Sugeno является более в вычислительном отношении эффективным по сравнению с процессом для системы Mamdani, поскольку он использует средневзвешенную или взвешенную сумму нескольких точек данных, а не вычисляет центроид двумерной области. [2]
Вы можете преобразовать систему Mamdani в систему Sugeno, используя convertToSugeno функция. Получившаяся система Sugeno имеет постоянные функции выхода принадлежности, которые соответствуют центроидам функций принадлежности выхода Mamdani.
Каждое правило в системе Sugeno работает, как показано на следующей схеме, которая показывает систему с двумя входами с входными значениями x и y.
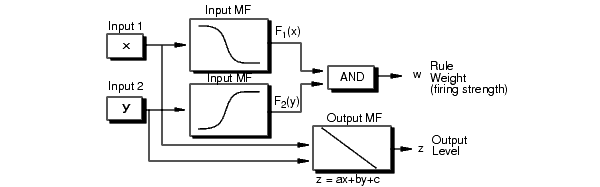
Каждое правило генерирует два значения:
zi - выходной уровень правила, который является либо постоянным значением, либо линейной функцией от входных значений:
Здесь x и y являются значениями входов 1 и 2, соответственно, и ai, bi и ci являются постоянными коэффициентами. Для системы Sugeno нулевого порядка zi является константой (a = b = 0).
wi - Сила стрельбы из правила, полученная из предшествующего правила
Здесь F 1 (...) и F 2 (...) являются функциями членства для входов 1 и 2, соответственно.
Выходы каждого правила являются взвешенным выходным уровнем, который является продуктом wi и zi.
Самый легкий способ визуализировать системы Sugeno первого порядка (a и b ненулевые) - это думать о каждом правиле как об определении местоположения движущегося синглтона. То есть одиночные выходы шипы могут перемещаться линейным образом в пределах выхода пространства, в зависимости от значений входа. Сила стрельбы правила затем определяет размер синглтонного шипа.
Конечным выходом системы является взвешенное среднее значение по всем выходам правил:
где N - количество правил.
Следующий рисунок показывает процесс нечеткого вывода для системы Sugeno.
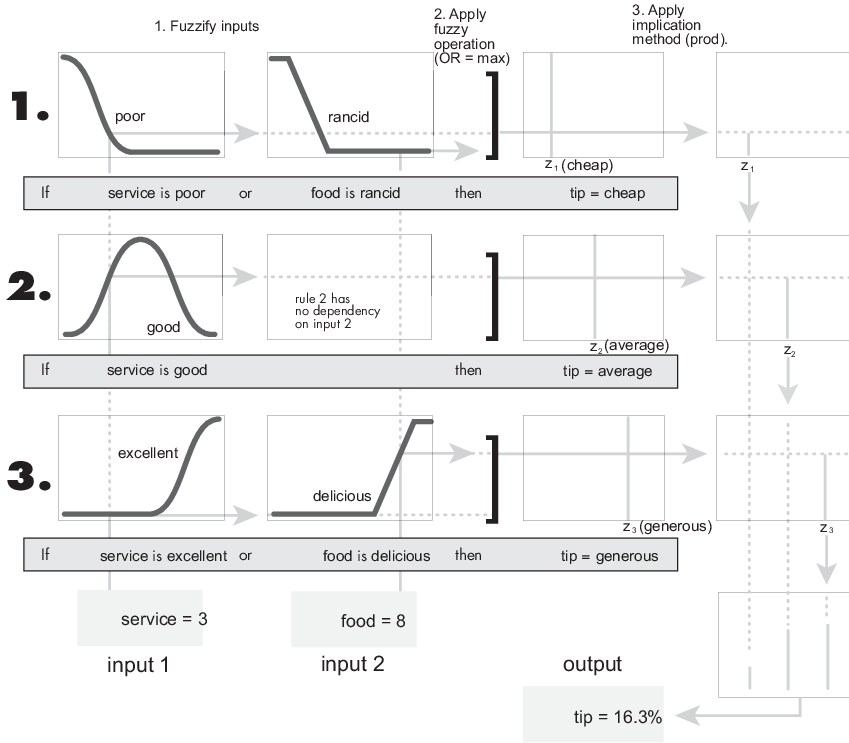
Примечание
Системы Sugeno всегда используют совокупность продуктов и сумм.
Из-за линейной зависимости каждого правила от входных переменных метод Sugeno идеально подходит для работы в качестве интерполирующего супервизора нескольких линейных контроллеров, которые должны применяться, соответственно, к различным условиям работы динамической нелинейной системы. Например, эффективность самолета может резко измениться с высотой и числом Маха. Линейные контроллеры, хотя и легко вычисляемые и подходящие для любого заданного рейса условия, должны обновляться регулярно и плавно, чтобы идти в ногу с изменением состояния рейса транспортного средства. Система нечеткого вывода Sugeno подходит для задачи плавной интерполяции линейных усилений, которые будут применяться через входное пространство; это естественный и эффективный планировщик усиления. Точно так же система Sugeno подходит для моделирования нелинейных систем путем интерполяции между несколькими линейными моделями.
[1] Mamdani, E.H., and S. Assilian. «An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller». International Journal of Man-Machine Studies 7, № 1 (январь 1975): 1-13. https://doi.org/10.1016/S0020-7373 (75) 80002-2.
[2] Sugeno, Michio, ed. промышленное применение нечеткого контроля. Амстердам; Нью-Йорк: Нью-Йорк, Нью-Йорк, США: Северо-Голландия; Единственные дистрибьюторы для США и Канады, Elsevier Science Pub. Ко, 1985.