Приведенный ступенчатый по строкам вид матрицы (Исключение по Гауссу-Жордану)
R = rref(A)A использование исключения по Гауссу-Жордану с частичным поворотом.
Создайте матрицу и вычислите приведенный ступенчатый по строкам вид матрицы. В этой форме матрица имеет начальное значение 1с в положении поворота каждого столбца.
A = magic(3)
A = 3×3
8 1 6
3 5 7
4 9 2
RA = rref(A)
RA = 3×3
1 0 0
0 1 0
0 0 1
Матрица магического квадрата 3 на 3 является полной рангом, поэтому приведенный ступенчатый по строкам вид матрицы является матрицей тождеств.
Теперь вычислите приведенный ступенчатый по строкам вид матрицы магической квадратной матрицы 4 на 4. Задайте два выхода, чтобы вернуть ненулевые сводные столбцы. Поскольку эта матрица неполного ранга, результат не является тождествами матрицей.
B = magic(4)
B = 4×4
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
[RB,p] = rref(B)
RB = 4×4
1 0 0 1
0 1 0 3
0 0 1 -3
0 0 0 0
p = 1×3
1 2 3
Используйте исключение по Гауссу-Жордану на дополненных матрицах, чтобы решить линейную систему и вычислить обратную матрицу. Эти методы в основном представляют академический интерес, поскольку существуют более эффективные и численно стабильные способы вычисления этих значений.
Создайте магическую квадратную матрицу 3 на 3. Добавьте дополнительный столбец в конец матрицы. Эта дополненная матрица представляет линейную систему , с дополнительным столбцом, соответствующим .
A = magic(3); A(:,4) = [1; 1; 1]
A = 3×4
8 1 6 1
3 5 7 1
4 9 2 1
Вычислите приведенный ступенчатый по строкам вид матрицы A. Индексируйте в R для извлечения записей в дополнительном (дополненном) столбце, который содержит решение для линейной системы.
R = rref(A)
R = 3×4
1.0000 0 0 0.0667
0 1.0000 0 0.0667
0 0 1.0000 0.0667
x = R(:,end)
x = 3×1
0.0667
0.0667
0.0667
Более эффективный способ решения этой линейной системы - это оператор обратной косой черты, x = A\b.
Создайте аналогичную матрицу магического квадрата, но на этот раз прибавьте матрицу тождеств того же размера к конечным столбцам.
A = [magic(3) eye(3)]
A = 3×6
8 1 6 1 0 0
3 5 7 0 1 0
4 9 2 0 0 1
Вычислите приведенный ступенчатый по строкам вид матрицы A. В этой форме дополнительные столбцы содержат обратную матрицу для магической квадратной матрицы 3 на 3.
R = rref(A)
R = 3×6
1.0000 0 0 0.1472 -0.1444 0.0639
0 1.0000 0 -0.0611 0.0222 0.1056
0 0 1.0000 -0.0194 0.1889 -0.1028
inv_A = R(:,4:end)
inv_A = 3×3
0.1472 -0.1444 0.0639
-0.0611 0.0222 0.1056
-0.0194 0.1889 -0.1028
Более эффективный способ вычисления обратной матрицы - это inv(A).
Рассмотрим линейную систему уравнений с четырьмя уравнениями и тремя неизвестными.
Создайте дополненную матрицу, которая представляет систему уравнений.
A = [1 1 5;
2 1 8;
1 2 7;
-1 1 -1];
b = [6 8 10 2]';
M = [A b];Использование rref для выражения системы в приведенный ступенчатый по строкам вид матрицы.
R = rref(M)
R = 4×4
1 0 3 2
0 1 2 4
0 0 0 0
0 0 0 0
Первые две строки R содержат уравнения, которые выражают и с точки зрения . Вторые две строки подразумевают, что существует по крайней мере одно решение, которое подходит для правого вектора (в противном случае одно из уравнений считалось бы ). Третий столбец не содержит центр, поэтому является независимой переменной. Поэтому существует бесконечно много решений для и , и может быть выбран свободно.
Для примера, если , затем и .
С числовой точки зрения более эффективный способ решения этой системы уравнений - это x0 = A\b, который (для прямоугольной матрицы A) вычисляет решение методом наименьших квадратов. В этом случае можно проверить точность решения с помощью norm(A*x0-b)/norm(b) и уникальность решения путем проверки, если rank(A) равен количеству неизвестных. Если существует более одного решения, то все они имеют форму , где - ядро пространства null(A) и может быть выбран свободно.
A - Входная матрицаВходная матрица.
Типы данных: single | double
Поддержка комплексного числа: Да
tol - Шарнирный допускmax(size(A))*eps*norm(A,inf) (по умолчанию) | скаляромДопуск поворота, заданный как скаляр. Если самый большой элемент (по абсолютному значению) в сводном столбце ниже допуска, столбец обнуляется. Это предотвращает деление и умножение с ненулевыми элементами поворота, меньшими, чем допуск.
Типы данных: single | double
R - Форма эшелона уменьшенного ряда AПриведенный ступенчатый по строкам вид матрицы из A, возвращается как матрица.
p - Ненулевые поворотные столбцыНенулевые сводные столбцы, возвращенные как вектор. Каждый элемент в p - индекс столбца A. Можно использовать p для оценки нескольких величин:
length(p) - оценка ранга A.
x(p) содержит переменные поворота в линейной системе Ax = b.
A(:,p) является базисом для области значений A.
R(1:r,p) является r-by- r единичная матрица, где r = length(p).
rank, orth, и null обычно являются более быстрыми и точными для вычисления ранга и базисных векторов матрицы.
mldivide рекомендуется для решения линейных систем.
Частичное вращение - это практика выбора элемента столбца с наибольшим абсолютным значением в столбце поворота, а затем обмена строками матрицы так, чтобы этот элемент находился в положении поворота (крайний левый ненулевой элемент в строке).
Для примера в матрице под алгоритмом начинается с определения наибольшего значения в первом столбце (значение в позиции (2,1), равное 1.1), а затем меняет полные первую и вторую строки так, чтобы это значение появилось в (1,1) положении.
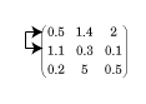
Использование частичного поворота в исключении Гауссова уменьшает (но не устраняет) ошибки округления в вычислении.
Матрица находится в форме эшелона строк, когда эти условия выполняются:
Все ненулевые строки находятся выше строк всех нулей.
Начальный коэффициент каждой строки находится строго справа от коэффициента в строке над ним.
Пример матрицы в форме эшелона строк
Дополнительные требования к приведенному ступенчатому по строкам виду матрицы:
Каждый начальный коэффициент должен быть 1 и должен быть единственным ненулевым в его столбце.
В то время как единичная матрица чаще всего связана с приведенным ступенчатым по строкам видом матрицы, другие формы возможны. Другой пример матрицы в приведенный ступенчатый по строкам вид матрицы
rref реализует исключение по Гауссу-Жордану с частичным поворотом. Допуск по умолчанию max(size(A))*eps*norm(A,inf) тесты на незначительные элементы столбца, которые обнулены для уменьшения ошибки округления.
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.