Оценка состояния контроллера

Переменные состояния контроллера

Когда контроллер работает, он использует свое текущее состояние, _xc, как базис для предсказаний. По определению вектор состояния является следующим:

$x_{c}^{T} (k) = [\begin{matrix} x_{p}^{T} (k) & x_{i d}^{T} (k) & \begin{matrix} x_{o d}^{T} (k) & x_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Вот,

_xc - состояние контроллера, включая _nxp + _nxid + _nxod + _nxn параметры состояния.
_xp - вектор состояния модели объекта управления, длиной _nxp.
_xid - вектор состояния входной модели возмущения длины _nxid.
_xod - вектор состояния выходной модели возмущения длины _nxod.
_xn - вектор состояния модели шума измерения, длины _nxn.

Таким образом, переменные, содержащие _xc, представляют модели, появляющиеся в следующей схеме системы MPC.

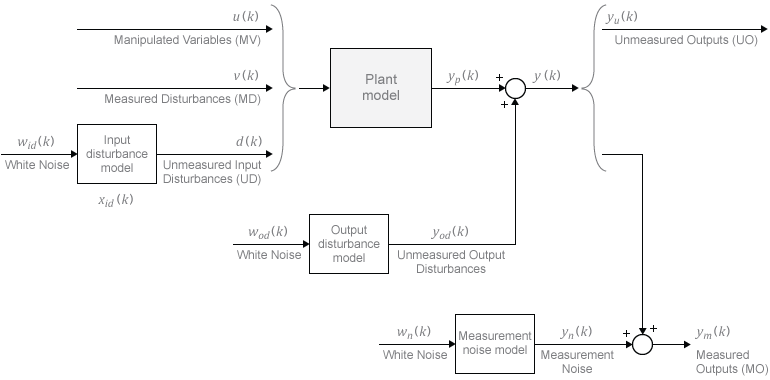
Некоторые векторы состояний могут быть пустыми. Если нет, они появляются в последовательности, заданной в каждой модели.

По умолчанию контроллер автоматически обновляет свое состояние с помощью последних измерений объекта. Для получения дополнительной информации см. раздел Оценка состояния. Кроме того, пользовательская функция оценки состояния позволяет вам обновить состояние контроллера с помощью внешней процедуры, а затем передать эти значения контроллеру. Для получения дополнительной информации см. раздел «Оценка пользовательского состояния».

Государственный наблюдатель

Комбинация моделей, показанных на схеме, приводит к наблюдателю состояния:

$\begin{matrix} x_{c} (k + 1) = A x_{c} (k) + B u_{o} (k) \\ y (k) = C x_{c} (k) + D u_{o} (k) . \end{matrix}$

Контроллер MPC использует наблюдатель состояния следующими способами:

Для оценки значений неизмеренных состояний, необходимых в качестве базиса для предсказаний (см. Оценку состояния).
Чтобы предсказать, как предложенные контроллером регулируемые переменные (MV) корректировки повлияют на будущие выходные значения объекта (см. «Предсказание выходных переменных»).

Входные сигналы наблюдателя являются безразмерным объектом, управляемым и измеренным нарушениями порядка, и белыми шумовыми входами в модели нарушения порядка и шума:

$u_{o}^{T} (k) = [\begin{matrix} u^{T} (k) & v^{T} (k) & \begin{matrix} \begin{matrix} w_{i d}^{T} (k) & w_{o d}^{T} (k) \end{matrix} & w_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Выходные параметры наблюдателя являются _ny безразмерными выходами объекта.

В терминах параметров, определяющих четыре модели, показанные на схеме, параметры наблюдателя:

$\begin{matrix} A = [\begin{matrix} A_{p} & B_{p d} C_{i d} & 0 & 0 \\ 0 & A_{i d} & 0 & 0 \\ 0 & 0 & A_{o d} & 0 \\ 0 & 0 & 0 & A_{n} \end{matrix}], & B = [\begin{matrix} B_{p u} & B_{p v} & B_{p d} D_{i d} & 0 & 0 \\ 0 & 0 & B_{i d} & 0 & 0 \\ 0 & 0 & 0 & B_{o d} & 0 \\ 0 & 0 & 0 & 0 & B_{n} \end{matrix}] \\ C = [\begin{matrix} C_{p} & D_{p d} C_{i d} & C_{o d} & [\begin{matrix} C_{n} \\ 0 \end{matrix}] \end{matrix}], & D = [\begin{matrix} 0 & D_{p v} & D_{p d} D_{i d} & D_{o d} & [\begin{matrix} D_{n} \\ 0 \end{matrix}] \end{matrix}] . \end{matrix},$

Здесь модели возмущения объекта управления и выхода переравниваются так, что измеренные выходы предшествуют неизмеренным выходам.

Оценка состояния

В целом состояния контроллера не измерены и должны быть оценены. По умолчанию контроллер использует установившийся фильтр Калмана, который выводится из наблюдателя состояния.

В начале k-го интервала управления состояние контроллера оценивается следующими шагами:

Получите следующие данные:
- _xc (k | k -1) - оценка состояния контроллера из предыдущих контрольных интервалов, k -1
- u^act(k -1) - Манипулируемая переменная (MV), фактически используемая на объекте с k-1 по k (принятая константа)
- u^opt(k -1) - Оптимальное СН, рекомендованное MPC и принятое к использованию на объекте от k -1 до k
- v (k) - Токовые измеренные нарушения порядка
- _ym ₍k) - Токовые выходы измеряемого объекта
- _Bu, _Bv - Столбцы B параметра наблюдателя, соответствующих u (k) и v (k) входам
- _Cm - Строки параметра наблюдателя C, соответствующего измеренным выходам объекта
- _Dmv - Строки и столбцы D параметра наблюдателя, соответствующих измеренным выходам объекта и измеренным входам нарушения порядка
- L, M - матрицы усиления Константа Калмана
Входной и выходной сигналы объекта масштабируются, чтобы быть безразмерными перед использованием в вычислениях.
Пересмотрите _xc (k | k -1), когда u^act(k -1) и u^opt(k -1) отличаются.
$x_{c}^{r e v} (k | k - 1) = x_{c} (k | k - 1) + B_{u} [u^{a c t} (k - 1) - u^{o p t} (k - 1)]$
Вычислите нововведение.
$e (k) = y_{m} (k) - [C_{m} x_{c}^{r e v} (k | k - 1) + D_{m v} v (k)]$
Обновите оценку состояния контроллера, чтобы принять во внимание последние измерения.

$x_{c} (k | k) = x_{c}^{r e v} (k | k - 1) + M e (k)$
Затем программное обеспечение использует _xc оценки текущего состояния (k | k), чтобы решить квадратичную программу с интервалом k. Решение является u^opt(k), рекомендуемое MPC значение переменной с манипуляциями, которое будет использоваться между контрольными интервалами k и k + 1.
Наконец, программное обеспечение готовится к следующему интервалу управления, принимая, что неизвестные входы _wid (k), _wod (k) и wn (k) принимают их среднее значение (ноль) между временами k и k + 1. Программное обеспечение предсказывает влияние известных входов и инноваций следующим образом:
$x_{c} (k + 1 | k) = A x_{c}^{r e v} (k | k - 1) + B_{u} u^{o p t} (k) + B_{v} v (k) + L e (k)$

Встроенный статический расчет коэффициента усиления Калмана

Программное обеспечение Model Predictive Control Toolbox™ использует kalman команда для вычисления коэффициентов усиления Оценки состояния фильтра Калмана L и M. Применяются следующие допущения:

Параметры наблюдателя состояния A, B, C, D являются инвариантными по времени.
Состояния контроллера, _xc, обнаруживаются. (Если нет, или если наблюдатель численно близок к неопределяемости, вычисление усиления Калмана прекращает работать, генерируя сообщение об ошибке.)
Стохастические входы _wid (k), _wod (k) и wn (k) являются независимыми белыми шумами, каждый с нулем среднего и единичной ковариации.
Дополнительные _wu белого шума (k) и _wv (k) с одинаковыми характеристиками складываются в безразмерные u (k) и v (k) входы соответственно. Это улучшает эффективность оценщика в некоторых случаях, например, когда модель объекта управления установки является нестабильной в разомкнутом контуре.

Без потери общности установите u (k) и v (k) входы в нуль. Эффект стохастических входов на состояниях контроллера и измеренных выходах объекта:

$\begin{matrix} x_{c} (k + 1) = A x_{c} (k) + B w (k) \\ y_{m} (k) = C_{m} x_{c} (k) + D_{m} w (k) . \end{matrix}$

Вот,

$w^{T} (k) = [\begin{matrix} w_{u}^{T} (k) & w_{v}^{T} (k) & \begin{matrix} \begin{matrix} w_{i d}^{T} (k) & w_{o d}^{T} (k) \end{matrix} & w_{n}^{T} (k) \end{matrix} \end{matrix}] .$

Входы в kalman команда являются параметрами A, _Cm и следующими ковариационными матрицами:

$\begin{matrix} Q = E {B w w^{T} B^{T}} = B B^{T} \\ R = E {D_{m} w w^{T} D_{m}^{T}} = D_{m} D_{m}^{T} \\ N = E {B w w^{T} D_{m}^{T}} = B D_{m}^{T} . \end{matrix}$

Здесь E {...} обозначает ожидание.

Выход переменных Предсказаний

Model Predictive Control требует предсказания выходов будущего объекта без шума, используемых в оптимизации. Это ключевое применение наблюдателя от государства (см. «Наблюдатель от государства»).

В k контрольного интервала требуемые данные следующие:

p - Горизонт предсказания (количество контрольных интервалов, которое больше или равно 1)
_xc (k | k) - оценки состояния контроллера (см. Оценка состояния)
v (k) - Токовые измеренные входы нарушения порядка (MD )
v (k + i | k) - Проектируемые будущие MD, где i = 1: p -1. Если вы не используете предварительный просмотр MD, то v (k + i | k) = v (k).
A, _Bu, _Bv, C, _Dv - Государственные константы наблюдателя, где _Bu, _Bv, и _Dv обозначают столбцы B и D матрицы, соответствующие входам u и v. _Du является нулевой матрицей из-за отсутствия прямого сквозного соединения

Предсказания предполагают, что неизвестные входы белого шума равны нулю (их ожидание). Кроме того, предсказанные выходы объекта должны быть свободными от шума. Таким образом, все члены, включающие состояния шума измерения, исчезают из уравнений наблюдателя состояния. Это эквивалентно обнулению последних _nxn элементов _xc (k | k).

Учитывая вышеуказанные данные и упрощения, для первого шага наблюдатель состояния предсказывает:

$x_{c} (k + 1 | k) = A x_{c} (k | k) + B_{u} u (k | k) + B_{v} v (k) .$

Продолжая для последующих шагов, i = 2: p, наблюдатель состояния предсказывает:

$x_{c} (k + i | k) = A x_{c} (k + i - 1 | k) + B_{u} u (k + i - 1 | k) + B_{v} v (k + i - 1 | k) .$

На любом шаге i = 1: p предсказанные выходы объекта без шума:

$y (k + i | k) = C x_{c} (k + i | k) + D_{v} v (k + i | k) .$

Все эти уравнения используют безразмерные входные и выходные переменные объекта. См. «Задание масштабных коэффициентов». Уравнения также принимают смещения нуля. Включение ненулевых смещений просто.

Для более быстрых расчетов контроллер MPC использует альтернативную форму вышеописанных уравнений, в которой вычисляются и сохраняются постоянные члены во время инициализации контроллера. См. матрицы QP.

См. также

kalman

Документация