Модельные прогнозирующие контроллеры используют модели объекта, нарушения порядка и шума для предсказания и оценки состояния. Структура модели, используемая в контроллере MPC, появляется на следующем рисунке.
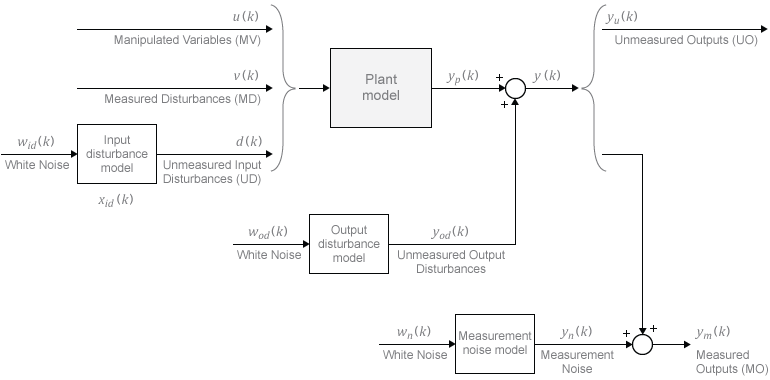
Можно задать модель объекта управления в одном из следующих форматов линейно-временной инвариантности (LTI):
Числовые модели LTI - Передаточная функция (tf), пространство состояний (ss), нули , полюса и усиления (zpk)
Идентифицированные модели (требует System Identification Toolbox™) - idss (System Identification Toolbox), idtf (System Identification Toolbox), idproc (System Identification Toolbox), и idpoly(Набор System Identification Toolbox)
Контроллер MPC выполняет все вычисления оценки и оптимизации с помощью переменных дискретного времени, без задержки, системы в пространстве состояний с безразмерными входами и выходом. Поэтому, когда вы задаете модель объекта управления в контроллере MPC, программное обеспечение при необходимости выполняет следующее:
Преобразование в пространство состояний - The ss команда преобразует предоставленную модель в модель пространства состояний LTI.
Дискретизация или повторная дискретизация - если шаг расчета модели отличается от шага расчета контроллера MPC (задано в Ts свойство), одно из следующих происходит:
Если модель является непрерывным временем, c2d команда преобразует его в объект LTI в дискретном времени с помощью шага расчета контроллером.
Если модель является дискретным временем, d2d команда повторяет его, чтобы сгенерировать объект LTI в дискретном времени, используя шаг расчета контроллером.
Удаление задержки - если модель в дискретном времени включает в себя какие-либо входные, выходные или внутренние задержки, absorbDelay команда заменяет их соответствующим количеством полюсов в z = 0, увеличивая общее количество дискретных состояний. The InputDelay, OutputDelay, и InternalDelay свойства полученной модели пространства состояний все равны нулю.
Преобразование в переменные без входа и выхода - контроллер MPC позволяет вам задать коэффициент шкалы для каждого объекта входа и выходной переменной. Если вы не задаете масштабные коэффициенты, они по умолчанию 1. Программа преобразует входную и выходную переменные объекта в безразмерную форму следующим образом:
где Ap, B, C и D являются постоянными матрицами пространства состояний с нулевой задержкой от шага 3 и:
Si является диагональю матрицей входа факторов шкалы в инженерных модулях.
So является диагональю матрицей выхода факторов шкалы в инженерных модулях.
xp - вектор состояния от шага 3 в инженерных модулях (включая любые поглощенные состояния задержки). Масштабирование переменных состояния не выполняется.
up является вектором безразмерных входных переменных объекта, включая манипулируемые переменные, измеренные нарушения порядка и неизмеренные входные нарушения порядка.
yp является вектором безразмерных выходных переменных объекта.
Получившаяся модель объекта управления имеет следующую эквивалентную форму:
Вот, Bpu, Bpv и Bpd являются соответствующими столбцами BSi. Кроме того, Dpu, Dpv и Dpd являются соответствующими столбцами . Наконец, u (k), v (k) и d (k) являются безразмерными манипулированными переменными, измеренными нарушениями порядка и неизмеренными входными нарушениями порядка, соответственно.
Контроллер MPC применяет ограничение Dpu = 0, что означает, что контроллер не допускает прямого сквозного соединения от какой-либо манипулированной переменной к какому-либо выходу объекта.
Если ваша модель объекта управления включает неизмеренные входные нарушения порядка, d (k), модель входного возмущения определяет тип сигнала и характеристики d (k). Смотрите Оценку Состояния Контроллера для получения дополнительной информации о модели.
getindist команда обеспечивает доступ к используемой модели.
Модель возмущения входа является ключевым фактором, который влияет на следующие атрибуты эффективности контроллера:
Динамическая реакция на явные нарушения порядка - символ отклика контроллера, когда измеренный выход объекта отклоняется от его предсказанной траектории, из-за неизвестного нарушения порядка или ошибки моделирования.
Асимптотическое отклонение устойчивых нарушений порядка - Если модель возмущения предсказывает устойчивое нарушение порядка, регулировки контроллера продолжаются, пока выход объекта не возвраты к желаемой траектории, эмулируя классический интегральный контроллер обратной связи.
Можно предоставить входную модель возмущения как пространство состояний LTI (ss), передаточная функция (tf), или нули , полюса и усиления (zpk) объект использование setindist. Контроллер MPC преобразует входную модель возмущения в систему в пространстве состояний LTI без задержки в дискретном времени с помощью тех же шагов, используемых для преобразования модели объекта управления. Результатом является:
где Aid, Bid, Cid и Did являются матрицами постоянного пространства состояний и:
xid (k) является вектором nxid ≥ 0 входных состояний модели возмущения.
dk (k) является вектором nd безразмерных неизмеренных входных нарушений порядка.
wid (k) является вектором nid ≥ 1 безразмерных белых шумовых входов, принятых с нулевым средним и единичным отклонением.
Если вы не предоставляете входную модель возмущения, то контроллер использует модель по умолчанию, которая имеет интеграторы с безразмерным усилением единства, добавленным к ее выходам. Для каждого неизмеренного входного нарушения порядка добавляется интегратор, если это не приведет к нарушению наблюдаемости состояния. В этом случае вместо этого используется статическая система с безразмерным усилением единицы.
Выход возмущения является частным случаем более общей модели входного возмущения. Его выход, yod (k), непосредственно добавляется к выходу объекта, а не влияет на состояния объекта. Выход возмущения задаёт тип сигнала и характеристики yod (k), и она часто используется на практике. Смотрите Оценку Состояния Контроллера для получения дополнительной информации о модели.
getoutdist команда обеспечивает доступ к используемой модели выходного возмущения.
Можно задать пользовательскую выходную модель возмущения как пространство состояний LTI (ss), передаточная функция (tf), или нули , полюса и усиления (zpk) объект использование setoutdist. Используя те же шаги, что и для модели объекта управления, контроллер MPC преобразует заданную выходную модель возмущения в дискретную, свободную от задержки, систему в пространстве состояний LTI. Результатом является:
где Aod, Bod, Cod и Dod являются матрицами постоянного пространства состояний и:
xod (k) является вектором nxod ≥ 1 выходов модели возмущения.
yod (k) является вектором безразмерных выходных нарушений порядка ny которые будут добавлены к безразмерным выходам объекта управления.
wod (k) является вектором nod безразмерных белых шумовых входов, принятых с нулевым средним и единичным отклонением.
Если вы не задаете выходную модель возмущения, то контроллер использует модель по умолчанию, которая имеет интеграторы с безразмерным усилением единства, добавленным к некоторым или всем ее выходам. Эти интеграторы добавляются согласно следующим правилам:
Нарушения порядка не оцениваются, то есть не добавляются интеграторы, для неизмеренных выходов объекта.
Для каждого измеренного выхода в порядке уменьшения выходного веса добавляется интегратор.
Для изменяющихся во времени весов для каждого выходного канала рассматривается сумма абсолютных значений с течением времени.
Для равных выходов весов выполняется порядок внутри вектора выхода.
Для каждого измеренного выхода интегратор не добавляется, если это привело бы к нарушению наблюдаемости состояния. Вместо этого используется коэффициент усиления со значением нуля.
Если существует модель входа возмущения, контроллер добавляет к этой модели любых интеграторов по умолчанию, прежде чем создавать модель выхода возмущения по умолчанию.
Одна из целей проектирования контроллера состоит в том, чтобы отличать нарушения порядка, которые требуют отклика, от шума измерения, который следует игнорировать. Модель шума измерения определяет ожидаемый тип и характеристики шума. Смотрите Оценку Состояния Контроллера для получения дополнительной информации о модели.
Используя те же шаги, что и для модели объекта управления, контроллер MPC преобразует модель шума измерения в дискретную систему в пространстве состояний LTI без задержки. Результатом является:
Здесь An, Bn, Cn и Dn являются матрицами постоянного пространства состояний и:
xn (k) является вектором nxn ≥ 0 состояний шумовой модели.
yn (k) является вектором nym шумовых сигналов без размерностей, которые добавляются к безразмерным измеренным выходам объекта.
wn (k) является вектором nn ≥ 1 безразмерных белых шумовых входов, принятых с нулевым средним и единичным отклонением.
Если вы не поставляете модель шума, по умолчанию это статический коэффициент усиления единицы: nxn = 0, Dn является единичной матрицей nym nym, и An, Bn и Cn пусты.
Для mpc объект контроллера, MPCobj, свойство MPCobj.Model.Noise обеспечивает доступ к модели шума измерения.
Примечание
Если минимальное собственное значение меньше 1x10–8, контроллер MPC добавляет 1x10–4 к каждому диагональному элементу Dn. Эта корректировка делает успешное вычисление усиления Калмана по умолчанию более вероятным.