Задача оптимизации

Обзор

Модель прогнозирующего управления решает задачу оптимизации - в частности, квадратичную программу (QP) - на каждом контрольном интервале. Решение определяет управляемые переменные (MV), которые будут использоваться на объекте до следующего контрольного интервала.

Эта задача QP включает следующие функции:

Цель, или «стоимость», функция - скаляр, неотрицательная мера эффективности контроллера, которая будет минимизирована.
Ограничения - Условия, которым должно удовлетворять решение, такие как физические ограничения на MV и выходные переменные объекта.
Решение - Корректировки СН, которые минимизируют функцию затрат и удовлетворяют ограничениям.

В следующих разделах эти функции описываются более подробно.

Функция стандартных затрат

Функция стандартной стоимости является суммой четырех членов, каждый из которых фокусируется на конкретном аспекте эффективности контроллера, следующим образом:

$J (z_{k}) = J_{y} (z_{k}) + J_{u} (z_{k}) + J_{Δ u} (z_{k}) + J_{ε} (z_{k}) .$

Здесь _zk решение QP. Как описано ниже, каждый термин включает веса, которые помогают вам сбалансировать конкурирующие цели. В то время как контроллер MPC обеспечивает веса по умолчанию, вам обычно нужно будет настроить их, чтобы настроить контроллер для вашего приложения.

Выход Отслеживания уставки

В большинстве приложений контроллер должен держать выбранные выходы объекта на уровне или около заданных базовых значений. Контроллер MPC использует следующую скалярную меру эффективности для выхода отслеживания уставки:

$J_{y} (z_{k}) = \sum_{j = 1}^{n_{y}} \sum_{i = 1}^{p} {\frac{w_{i, j}^{y}}{s_{j}^{y}} [r_{j} (k + i | k) - y_{j} (k + i | k)]}^{2} .$

Вот,

k - Ток контрольного интервала.
p - Горизонт предсказания (количество интервалов).
_ny - Количество выходных переменных объекта.
_zk - решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_yj (k + i | k) - Прогнозируемое значение j-го завода на i-м шаге горизонта прогнозирования, в инженерных единицах.
_rj (k + i | k) - Базовое значение для j-го завода на i-м шаге горизонта прогнозирования, в инженерных единицах.
$s_{j}^{y}$ - Масштабный коэффициент для j-го объекта, в инженерных модулях.
$w_{i, j}^{y}$ - Вес настройки для j объекта на i шаге предсказания (безразмерный).

Значения _ny, p, $s_{j}^{y}$ , и $w_{i, j}^{y}$ являются постоянными спецификациями контроллера. Контроллер получает опорные значения _rj (k + i | k) для всего горизонта предсказания. Контроллер использует наблюдатель состояния, чтобы предсказать _{выходные параметры} объекта, yj (k + i | k), которые зависят от манипулированных _{переменных корректировок} (zk), измеренных возмущений (MD) и оценок состояния. Через k интервал доступны оценки состояния контроллера и значения MD. _{Поэтому} Jy является _{функцией} только zk.

Отслеживание манипулированных переменных

В некоторых приложениях, таких как когда манипулируемых переменных больше, чем выходных параметров объекта выходов, контроллер должен держать выбранные манипулируемые переменные (MV) на уровне или около заданных целевых значений. Контроллер MPC использует следующий скалярный показатель эффективности для отслеживания манипулируемых переменных:

$J_{u} (z_{k}) = \sum_{j = 1}^{n_{u}} \sum_{i = 0}^{p - 1} {\frac{w_{i, j}^{u}}{s_{j}^{u}} [u_{j} (k + i | k) - u_{j, t a r g e t} (k + i | k)]}^{2} .$

Вот,

k - Ток контрольного интервала.
p - Горизонт предсказания (количество интервалов).
_nu - Количество манипулируемых переменных.
_zk - решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_uj,target (k + i | k) - целевое значение для j-го МВ на i-м предсказания шаге горизонта, в инженерных модулях.
$s_{j}^{u}$ - Масштабный коэффициент для j-го СН, в инженерных модулях.
$w_{i, j}^{u}$ - Настройка веса для j-го МВ на i-м шаге предсказания (безразмерный).

Значения _nu, p, $s_{j}^{u}$ , и $w_{i, j}^{u}$ являются постоянными спецификациями контроллера. Контроллер получает _uj,target (k + i | k) значения для всего горизонта. Контроллер использует наблюдатель состояния, чтобы предсказать выходы объекта. _{Таким образом}, Ju является функцией только zk.

Управляемая переменная Подавление Перемещения

Большинство приложений предпочитают небольшие регулировки СН (moves). Константа MPC использует следующее скалярное измерение эффективности для управляемого подавления перемещения:

$J_{Δ u} (z_{k}) = \sum_{j = 1}^{n_{u}} \sum_{i = 0}^{p - 1} {\frac{w_{i, j}^{Δ u}}{s_{j}^{u}} [u_{j} (k + i | k) - u_{j} (k + i - 1 | k)]}^{2} .$

Вот,

k - Ток контрольного интервала.
p - Горизонт предсказания (количество интервалов).
_nu - Количество манипулируемых переменных.
_zk - решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
$s_{j}^{u}$ - Масштабный коэффициент для j-го СН, в инженерных модулях.
$w_{i, j}^{Δ u}$ - Настройка веса для j-го движения СН на i-м шаге предсказания (безразмерный).

Значения _nu, p, $s_{j}^{u}$ , и $w_{i, j}^{Δ u}$ являются постоянными спецификациями контроллера. u (k -1 | k) = u (k -1), которые являются известными MV из предыдущих _{контрольных интервалов}. JΔu является _{функцией} только zk.

В сложение, управляемый горизонт m < p (или блокировка MV) ограничивает определенные движения MV равными нулю.

Нарушение ограничений

На практике нарушения ограничений могут быть неизбежными. Мягкие ограничения допускают допустимое решение QP при таких условиях. Контроллер MPC использует переменную slack без размерности, неотрицательную _εk, которая количественно определяет нарушение ограничений в худшем случае. (См. Ограничения) Соответствующий показатель эффективности:

$J_{ε} (z_{k}) = ρ_{ε} ε_{k}^{2} .$

Вот,

_zk - решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_εk - Переменная Slack в контрольный интервал k (без размерности).
_ρε - вес штрафа за нарушение ограничений (безразмерный).

Функция альтернативных затрат

Можно выбрать использование следующей альтернативы функции стандартных затрат:

$J (z_{k}) = \sum_{i = 0}^{p - 1} {[e_{y}^{T} (k + i) Q e_{y} (k + i)] + [e_{u}^{T} (k + i) R_{u} e_{u} (k + i)] + [Δ u^{T} (k + i) R_{Δ u} Δ u (k + i)]} + ρ_{ϵ} ε_{k}^{2} .$

Здесь Q (_ny -by- ny), Ru и _RΔu ₍nu -_by- nu) являются положительно-полуопределенными матрицами веса, и:

$\begin{matrix} e_{y} (i + k) = S_{y}^{- 1} [r (k + i + 1 | k) - y (k + i + 1 | k)] \\ e_{u} (i + k) = S_{u}^{- 1} [u_{t a r g e t} (k + i | k) - u (k + i | k)] \\ Δ u (k + i) = S_{u}^{- 1} [u (k + i | k) - u (k + i - 1 | k)] . \end{matrix}$

Также,

_Sy - Диагональная матрица переменных масштабных коэффициентов продукции объекта, в технических модулях.
_Su - Диагональная матрица шкальных коэффициентов СН в инженерных модулях.
r (k + 1 | k₎ - ny исходные значения продукции завода на i-м шаге горизонта прогнозирования, в инженерных единицах.
y (k + 1 | k₎ - ny выходы объекта на i-м шаге горизонта прогнозирования, в инженерных единицах.
_zk - решение QP, данное:
$z_{k}^{T} = [\begin{matrix} u {(k | k)}^{T} & u {(k + 1 | k)}^{T} & \dots & u {(k + p - 1 | k)}^{T} & ε_{k} \end{matrix}] .$
_utarget (k + i | k₎ - nu целевые значения СН, соответствующие u (k + i | k), в инженерных единицах.

Выходные предсказания используют наблюдатель состояния, как в функции стандартных затрат.

Альтернативная функция стоимости позволяет недиагональное взвешивание, но требует, чтобы веса были идентичны на каждом шаге горизонта предсказания.

Функции альтернативных и стандартных затрат идентичны, если выполняются следующие условия:

В функциях стандартных затрат используются веса $w_{i, j}^{y}$ , $w_{i, j}^{u}$ , и $w_{i, j}^{Δ u}$ которые являются постоянными относительно индекса, i = 1: p.
Матрицы Q, _Ru и _RΔu диагональны с квадратами этих весов как диагональные элементы.

Ограничения

Некоторые ограничения неявны. Например, m управляющего горизонта < p (или блокировка MV) заставляет некоторые шаги MV быть нулем, и наблюдатель состояния, используемый для предсказания выхода объекта, является набором неявных ограничений равенства. Явные ограничения, которые можно настроить, описаны ниже.

Ограничения на выходах объекта, MV и шагах MV

Наиболее распространенными ограничениями MPC являются ограничения, следующие.

$\begin{matrix} \frac{y_{j, m i n} (i)}{s_{j}^{y}} - ε_{k} V_{j, m i n}^{y} (i) \leq \frac{y_{j} (k + i | k)}{s_{j}^{y}} \leq \frac{y_{j, m a x} (i)}{s_{j}^{y}} + ε_{k} V_{j, m a x}^{y} (i), i = 1 : p, j = 1 : n_{y} \\ \frac{u_{j, m i n} (i)}{s_{j}^{u}} - ε_{k} V_{j, m i n}^{u} (i) \leq \frac{u_{j} (k + i - 1 | k)}{s_{j}^{u}} \leq \frac{u_{j, m a x} (i)}{s_{j}^{u}} + ε_{k} V_{j, m a x}^{u} (i), i = 1 : p, j = 1 : n_{u} \\ \frac{Δ u_{j, m i n} (i)}{s_{j}^{u}} - ε_{k} V_{j, m i n}^{Δ u} (i) \leq \frac{Δ u_{j} (k + i - 1 | k)}{s_{j}^{u}} \leq \frac{Δ u_{j, m a x} (i)}{s_{j}^{u}} + ε_{k} V_{j, m a x}^{Δ u} (i), i = 1 : p, j = 1 : n_{u} . \end{matrix}$

Здесь параметры V (значения ECR) являются безразмерными константами контроллера, аналогичными весам функции затрат, но используемыми для смягчения ограничений (см. «Смягчение ограничений»). Также,

_εk - скаляр QP slack (без размерности), используемая для смягчения ограничений.
$s_{j}^{y}$ - Масштабный коэффициент для j-го объекта, в инженерных модулях.
$s_{j}^{u}$ - Масштабный коэффициент для j-го СН, в инженерных модулях.
y _{j, мин} (i)_{, y j}, макс (i) - нижняя и верхняя границы для j-го завода на i-м шаге прогнозирования горизонта, в инженерных единицах.
u _{j, мин} (i)_{, u j}, макс (i) - нижняя и верхняя границы для j-го МВ на i-м предсказания шаге горизонта, в инженерных модулях.
Δu _{j, мин} (i), _{Δu j}, макс (i) - нижняя и верхняя границы для j-го шага МВ на i-м предсказания шаге горизонта, в инженерных модулях.

За исключением условия неотрицательности переменной slack, все вышеуказанные ограничения являются необязательными и по умолчанию неактивны (то есть инициализированы бесконечными ограничивающими значениями). Чтобы включить ограничение привязки, необходимо задать конечный предел при проектировании контроллера.

Матрицы QP

В этом разделе описываются матрицы, связанные с задачей оптимизации прогнозирующего управления модели, описанной в Задаче Оптимизации.

Предсказание

Предположим, что модели возмущения, описанные в Входе входного возмущения, являются единичными усилениями; то есть d (k) = _nd (k) является белым Гауссовым шумом. Можно обозначить эту задачу как

$x \leftarrow [\begin{matrix} x \\ x_{d} \end{matrix}], A \leftarrow [\begin{matrix} A & B_{d} \bar{C} \\ 0 & \bar{A} \end{matrix}], B_{u} \leftarrow [\begin{matrix} B_{u} \\ 0 \end{matrix}], B_{v} \leftarrow [\begin{matrix} B v \\ 0 \end{matrix}], B_{d} \leftarrow [\begin{matrix} B_{d} \bar{D} \\ \bar{B} \end{matrix}], C \leftarrow [\begin{matrix} C & D_{d} \bar{C} \end{matrix}]$

Затем модель предсказания:

x (k +1) = <reservedrangesplaceholder11> <reservedrangesplaceholder10> (<reservedrangesplaceholder9>) + <reservedrangesplaceholder8> <reservedrangesplaceholder7> (<reservedrangesplaceholder6>) +<reservedrangesplaceholder5><reservedrangesplaceholder4>(<reservedrangesplaceholder3>)+<reservedrangesplaceholder2><reservedrangesplaceholder1>(<reservedrangesplaceholder0>)

y (<reservedrangesplaceholder9>) = <reservedrangesplaceholder8> <reservedrangesplaceholder7> (<reservedrangesplaceholder6>) + <reservedrangesplaceholder5> <reservedrangesplaceholder4> (<reservedrangesplaceholder3>) + <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>)

Далее рассмотрим задачу предсказания будущих траекторий модели, выполненных в момент времени k = 0. Установите nd (i) = 0 для всех моментов предсказания i и получите

$y (i | 0) = C [A^{i} x (0) + \sum_{h = 0}^{i - 1} A^{i - 1} (B_{u} (u (- 1) + \sum_{j = 0}^{h} Δ u (j)) + B_{v} v (h))] + D_{v} v (i)$

Это уравнение дает решение

$[\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] = S_{x} x (0) + S_{u 1} u (- 1) + S_{u} [\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] + H_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}]$

где

$\begin{array}{l} S_{x} = [\begin{matrix} C A \\ C A^{2} \\ \dots \\ C A^{p} \end{matrix}] \in ℜ^{p n_{y} \times n_{x}}, S_{u 1} = [\begin{matrix} C B_{u} \\ C B_{u} + C A B_{u} \\ \dots \\ \sum_{h = 0}^{p - 1} C A^{h} B_{u} \end{matrix}] \in ℜ^{p n_{y} \times n_{u}} \\ S_{u} = [\begin{matrix} C B_{u} & 0 & \dots & 0 \\ C B_{u} + C A B_{u} & C B_{u} & \dots & 0 \\ \dots & \dots & \dots & \dots \\ \sum_{h = 0}^{p - 1} C A^{h} B_{u} & \sum_{h = 0}^{p - 2} C A^{h} B_{u} & \dots & C B_{u} \end{matrix}] \in ℜ^{p n_{y} \times p n_{u}} \\ H_{v} = [\begin{matrix} C B_{v} & D_{v} & 0 & \dots & 0 \\ C A B_{v} & C B_{v} & D_{v} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots \\ C A^{p - 1} B_{v} & C A^{p - 2} B_{v} & C A^{p - 3} B_{v} & \dots & D_{v} \end{matrix}] \in ℜ^{p n_{y} \times (p + 1) n_{v}} . \end{array}$

Переменные оптимизации

Предположим m - количество свободных ходов управления, и предположим z = [_z0;...; zm-1]. Затем,

$[\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] = J_{M} [\begin{matrix} z_{0} \\ \dots \\ z_{m - 1} \end{matrix}]$

где J M зависит от выбора блокирующих ходов. Вместе с ɛ переменной slack, векторы _z 0,..., _{z m} -1 составляют свободные переменные оптимизации задачи оптимизации. В случае систем с одной манипулированной переменной_, z 0,..._{, z} m -1 являются скалярами.

Рассмотрим блокирующие движения, изображенные на следующем графике.

Блокирование перемещений: входы и входные шаги для перемещений = [2 3 2]

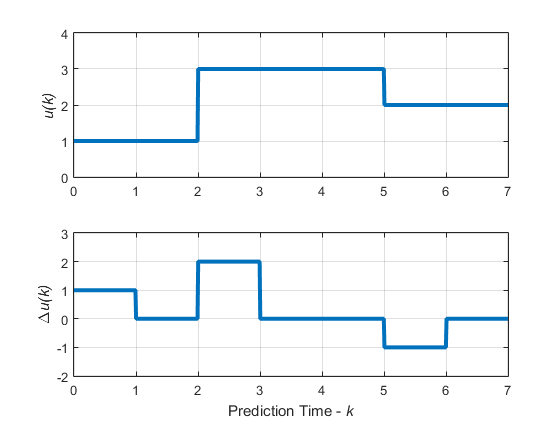
Этот график соответствует выбору moves=[2 3 2], или эквивалентно, u (0) = u (1), u (2) = u (3) = u (4), u (5) = u (6),

Затем соответствующая матрица _JM является

$J_{M} = [\begin{matrix} I & 0 & 0 \\ 0 & 0 & 0 \\ 0 & I & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & I \\ 0 & 0 & 0 \end{matrix}]$

Для получения дополнительной информации о манипулированных блокировках переменных смотрите Манипулированные блокировки переменных.

Функция затрат

Стандартная форма. Функция, которая будет оптимизирована,

$\begin{array}{l} J (z, ε) = {([\begin{matrix} u (0) \\ \dots \\ u (p - 1) \end{matrix}] - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}])}^{T} W_{u}^{2} ([\begin{matrix} u (0) \\ \dots \\ u (p - 1) \end{matrix}] - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]) + {[\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}]}^{T} W_{Δ u}^{2} [\begin{matrix} Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] \\ + {([\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}])}^{T} W_{y}^{2} ([\begin{matrix} y (1) \\ \dots \\ y (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]) + ρ_{ε} ε^{2} \end{array}$

где

\begin{matrix} W_{u} = diag (w_{0, 1}^{u}, w_{0, 2}^{u}, ..., w_{0, n_{u}}^{u}, ..., w_{p - 1, 1}^{u}, w_{p - 1, 2}^{u}, ..., w_{p - 1, n_{u}}^{u}) \\ W_{Δ u} = diag (w_{0, 1}^{Δ u}, w_{0, 2}^{Δ u}, ..., w_{0, n_{u}}^{Δ u}, ..., w_{p - 1, 1}^{Δ u}, w_{p - 1, 2}^{Δ u}, ..., w_{p - 1, n_{u}}^{Δ u}) \\ W_{y} = diag (w_{1, 1}^{y}, w_{1, 2}^{y}, ..., w_{1, n_{y}}^{y}, ..., w_{p, 1}^{y}, w_{p, 2}^{y}, ..., w_{p, n_{y}}^{y}) \end{matrix}

(1)

Наконец, после замены u (k), Δu (k), y (k), J (z) может быть переписан как

\begin{array}{l} J (z, ε) = ρ_{ε} ε^{2} + z^{T} K_{Δ u} z + 2 ({[\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]}^{T} K_{r} + {[\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}]}^{T} K_{v} + u {(- 1)}^{T} K_{u} + {[\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]}^{T} K_{u t} + x {(0)}^{T} K_{x}) z \\ + c_{y}^{T} W_{y} c_{y} + c_{u}^{T} W_{u} c_{u} \end{array}

(2)

где

$\begin{array}{l} c_{y} = S_{x} x (0) + S_{u 1} u (- 1) + H_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] - [\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}] \\ c_{u} = [\begin{matrix} I_{1} \\ \dots \\ I_{p} \end{matrix}] u (- 1) - [\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}] \end{array}$

Здесь I 1 =... = I p являются тождествами матрицами _{размера} nu.

Примечание

Вы можете захотеть, чтобы задача QP оставалась строго выпуклой. Если число обусловленности матрицы Гессия _{KИ U} больше 10¹², добавить количество 10*sqrt(eps) на каждом диагональном термине. Вы можете использовать это решение только, когда все входные скорости неенализированы (W^Δ^u= 0) (см. Weights свойство mpc объект).

Функция альтернативных затрат. Если вы используете альтернативную функцию стоимости, показанную в Альтернативной функции стоимости, то Уравнение 1 заменяется следующим:

\begin{array}{l} W_{u} = blkdiag (R_{u}, ..., R_{u}) \\ W_{Δ u} = blkdiag (R_{Δ u}, ..., R_{Δ u}) \\ W_{y} = blkdiag (Q, ..., Q) \end{array}

(3)

В этом случае блочно-диагональные матрицы повторяют p раз, например, один раз для каждого шага в горизонте предсказания.

У вас также есть опция использовать комбинацию стандартной и альтернативной форм. Для получения дополнительной информации смотрите Weights свойство mpc объект.

Ограничения

Затем рассмотрим пределы входных входов, входных шагов и выходов наряду с ограничением ɛ≥ 0.

$[\begin{matrix} y_{\min} (1) - ε V_{\min}^{y} (1) \\ \dots \\ y_{\min} (p) - ε V_{\min}^{y} (p) \\ u_{\min} (0) - ε V_{\min}^{u} (0) \\ \dots \\ u_{\min} (p - 1) - ε V_{\min}^{u} (p - 1) \\ Δ u_{\min} (0) - ε V_{\min}^{Δ u} (0) \\ \dots \\ Δ u_{\min} (p - 1) - ε V_{\min}^{Δ u} (p - 1) \end{matrix}] \leq [\begin{matrix} y (1) \\ \dots \\ y (p) \\ u (0) \\ \dots \\ u (p - 1) \\ Δ u (0) \\ \dots \\ Δ u (p - 1) \end{matrix}] \leq [\begin{matrix} y_{\max} (1) + ε V_{\max}^{y} (1) \\ \dots \\ y_{\max} (p) + ε V_{\max}^{y} (p) \\ u_{\max} (0) + ε V_{\max}^{u} (0) \\ \dots \\ u_{\max} (p - 1) + ε V_{\max}^{u} (p - 1) \\ Δ u_{\max} (0) + ε V_{\max}^{Δ u} (0) \\ \dots \\ Δ u_{\max} (p - 1) + ε V_{\max}^{Δ u} (p - 1) \end{matrix}]$

Примечание

Чтобы уменьшить вычислительные усилия, контроллер автоматически устраняет посторонние ограничения, такие как бесконечные границы. Таким образом, ограничительное множество, используемый в реальном времени, может быть намного меньше, чем предложено в этом разделе.

Подобно тому, что вы сделали для функции затрат, можно заменить u (k),

M_{z} z + M_{ε} ε \leq M_{\lim} + M_{v} [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] + M_{u} u (- 1) + M_{x} x (0)

(4)

В этом случае матрицы _Mz, Mɛ, Mlim, _Mv, _Mu и _Mx получаются из верхней и нижней границ и значений ECR.

Без ограничений Модели прогнозирующее управление

Оптимальное решение вычисляется аналитически

$z * = - K_{Δ u}^{- 1} {({[\begin{matrix} r (1) \\ \dots \\ r (p) \end{matrix}]}^{T} K_{r} + [\begin{matrix} v (0) \\ \dots \\ v (p) \end{matrix}] K_{v} + u {(- 1)}^{T} K_{u} + {[\begin{matrix} u_{t a r g e t} (0) \\ \dots \\ u_{t a r g e t} (p - 1) \end{matrix}]}^{T} K_{u t} + x {(0)}^{T} K_{x})}^{T}$

и моделирующий прогнозирующий контроллер устанавливает Β u (k) = z * 0, u (k) = u (k-1) + Üu (k).

Документация