Manipulated variable blocking является альтернативой более простой концепции горизонта управления (см. «Выбор шага расчета» и «Горизонты»), и имеет много одинаковых преимуществ. Манипулирование блокировкой переменной:
Обеспечивает большую гибкость настройки
Может сглаживать манипулированные переменные корректировки
Может улучшить робастность контроллера
Чтобы использовать манипулированное блокирование переменных, разделите горизонт предсказания на ряд интервалов блокирования, задав свой горизонт управления как вектор размеров блоков [m 1, m 2,...]. Сумма размеров блоков должна совпадать с p горизонта предсказания. Если вы задаете вектор, сумма которого:
Меньше, чем горизонт предсказания, тогда контроллер добавляет интервал блокировки. Длина этого интервала такова, что сумма длин интервала p. Для примера, если p = 10 и вы задаете контрольный горизонт m = [1 2 3], затем контроллер использует четыре интервала с длинами [1 2 3 4].
Больше горизонта предсказания, затем интервалы усекаются до тех пор, пока сумма длин интервалов не будет равна p. Для примера, если p = 10 и вы задаете контрольный горизонт [1 2 3 6 7], затем контроллер использует четыре интервала с длинами [1 2 3 4].
Контроллер вычисляет M свободные ходы, где M количество интервалов блокировки. Первое бесплатное движение относится ко временам k через k + <reservedrangesplaceholder6> 1-1, второе бесплатное движение применяется со времени k + <reservedrangesplaceholder4> 1 через k + <reservedrangesplaceholder2> 1 + <reservedrangesplaceholder1> 2-1 и так далее. Здесь k текущий контрольный интервал.
По умолчанию контроллер затем содержит управляемую переменную константу в каждом блоке; то есть управляющие перемещения являются кусочно-постоянными на каждом интервале. Для примера следующий рисунок показывает оптимальные движения управления для горизонта управления m = [2 3 2] и предсказание горизонт p = 7.
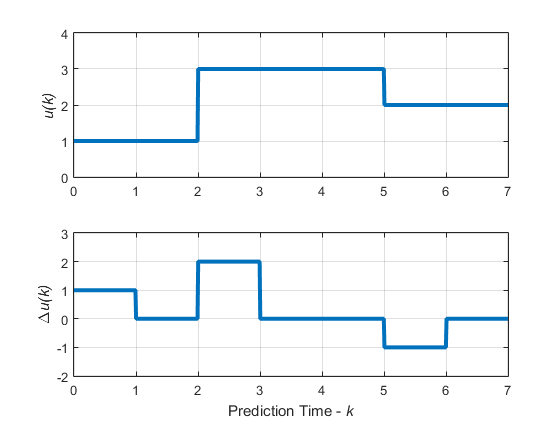
Для каждого блока манипулируемая переменная, u, является постоянной, то есть:
u (0) = u (1)
u (2) = u (3) = u (4)
u (5) = u (6)
Рекомендуемый подход к блокировке состоит в том, чтобы разделить горизонт предсказания на 3-5 блоков и использовать одну из следующих альтернативных блокировок:
Равные размеры блоков (от одной пятой до одной трети горизонта предсказания, p)
Размеры блоков увеличиваются. Для примера с p = 20можно попробовать три блока с интервалами длины 3, 7 и 10.
Чтобы протестировать эффекты различных манипулированных строений блокировки переменных, выполните тесты симуляции с обратной связью при следующих условиях:
Никаких ограничений
Нет ошибки предсказания; то есть модель предсказания контроллера должна быть идентичной модели объекта управления
Чтобы проверить каждый контроллер на стабильность и робастность, используйте review функция.
Как и в случае с линейным контроллером MPC, когда вы используете манипулированную блокировку переменных, нелинейный контроллер MPC использует кусочно-постоянные интервалы блокировки по умолчанию. Этот подход часто является слишком ограничительным для оптимальных приложений планирования пути. Чтобы создать менее ограниченную, лучше обусловленную нелинейную задачу программирования, можно задать кусочно-линейные манипулируемые интервалы блокирования переменных. Для этого установите Optimization.MVInterpolationOrder свойство вашего nlmpc объект контроллера, для 1.
Следующий рисунок показывает оптимальные движения управления для горизонта управления m = [2 3 2] и горизонт предсказания p = 7.
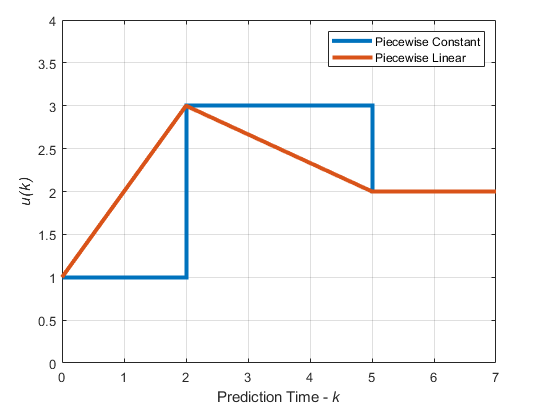
В кусочно-постоянном случае по умолчанию вычисленные манипулированные значения переменных 1, 3, и 2 являются постоянными на их соответствующих блокирующих интервалах.
В кусочно-линейном случае вычисленные манипулируемые значения переменных линейно интерполируются для первых двух интервалов блокирования и остаются постоянными для последнего интервала.
Для получения дополнительной информации о нелинейных контроллерах MPC, смотрите Нелинейный MPC.
Примечание
Линейная интерполяция блокирующих движений не поддерживается неявными, адаптивными или запланированными по усилению контроллерами MPC.