Задайте ограничения

Входные и выходные ограничения

По умолчанию, когда вы создаете объект контроллера, используя mpc команда, никаких ограничений не существует. Чтобы включить ограничение, задайте соответствующее свойство контроллера. В следующей таблице представлены свойства контроллера, используемые для определения большинства ограничений MPC. (MV = переменная, управляемая объектом; OV = выходная переменная объекта; Шаг МВ = u (k) - u (k - 1).

Ограничение	Свойство контроллера	Смягчение ограничений
Нижняя граница i th MV	`MV(i).Min > -Inf`	`MV(i).MinECR > 0`
Верхняя граница i-го СН	`MV(i).Max < Inf`	`MV(i).MaxECR > 0`
Нижняя граница i OV	`OV(i).Min > -Inf`	`OV(i).MinECR > 0`
Верхняя граница i OV	`OV(i).Max < Inf`	`OV(i).MaxECR > 0`
Нижняя граница на i-м шаге MV	`MV(i).RateMin > -Inf`	`MV(i).RateMinECR > 0`
Верхняя граница на i-м шаге MV	`MV(i).RateMax < Inf`	`MV(i).RateMaxECR > 0`

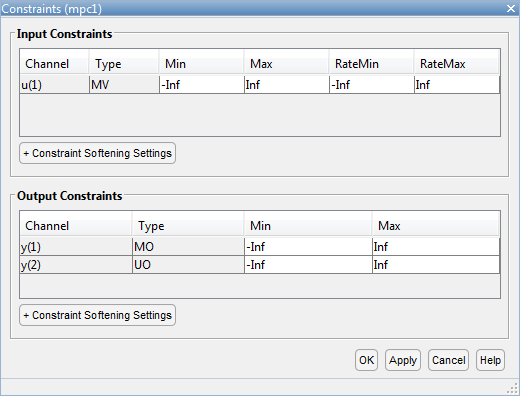
Чтобы задать свойства ограничения контроллера с помощью приложения MPC Designer, на вкладке Tuning, нажмите Constraints. В диалоговом окне «Ограничения» задайте значения ограничений.

Смотрите Ограничения для уравнений, описывающих соответствующие ограничения.

Совет

Для границ СН:

Включите известные физические пределы на MV объекта в качестве жестких границ MV.
Включите ограничения с шагом MV, когда существует известный физический предел скорости изменения, или ваше приложение требует, чтобы вы предотвратили большие шаги по какой-либо другой причине.
Не включать как жесткие ограничения MV, так и жесткие ограничения с шагом MV на том же MV, так как они могут конфликтовать. Если оба типа границ важны, смягчите один.

Для OV-границ:

Не включать ограничения OV, если они не необходимы для вашего приложения. В качестве альтернативы установке OV-привязки можно задать OV- ссылки и установить его вес функции затрат, чтобы сохранить OV рядом с его уставкой.
Все ограничения OV должны быть смягчены.
Рассмотрите возможность оставить OV без ограничений для некоторых шагов горизонта предсказания. Смотрите изменяющиеся во времени веса и ограничения.
Рассмотрим изменяющееся во времени ограничение OV, которое легко удовлетворить в начале горизонта, постепенно сходя к более строгому ограничению. Смотрите изменяющиеся во времени веса и ограничения.
Не включать OV-ограничения, которые невозможно удовлетворить. Даже при мягкости такие ограничения могут вызвать неожиданное поведение контроллера. Для примера рассмотрим объект SISO с пятью периодами дискретизации с задержкой. OV-ограничение перед шестым шагом горизонта предсказания, в целом, невозможно удовлетворить. Вы можете использовать review команда, чтобы проверить на такие невозможные ограничения и использовать изменяющуюся во времени OV привязку. Смотрите изменяющиеся во времени веса и ограничения.

Смягчение ограничений

Hard ограничения являются ограничениями, которым должно удовлетворять решение квадратичного программирования (QP). Если математически невозможно удовлетворить жесткому ограничению на заданном контрольном интервале, k, QP infeasible. В этом случае контроллер возвращает состояние ошибки и устанавливает управляемые переменные (MV) на u (k) = u (k -1), то есть без изменений. Если условие, приводящее к недопустимости, не разрешено, недопустимость может продолжаться бесконечно, что приводит к потере контроля.

Нарушения порядка и ошибки предсказания неизбежны на практике. Поэтому на объекте может возникнуть нарушение ограничений, хотя контроллер предсказывает обратное. Допустимое решение QP не гарантирует, что все жесткие ограничения будут удовлетворены, когда на объекте используется оптимальное СН.

Если единственными ограничениями в вашем приложении являются ограничения на MV, ограничения MV могут быть жесткими ограничениями, так как они по умолчанию. Только ограничения MV не могут вызвать недопустимость. То же самое верно, когда единственные ограничения связаны с шагами СН.

Однако жесткая граница СН с жестким ограничением шага СН может привести к недопустимости. Для примера нарушение или операция под ручным управлением могут привести к тому, что фактическое СН, используемое в объект, превысит заданную границу во время интервала k -1. Если контроллер находится в автоматическом режиме во время k интервала, он должен вернуть MV значение в пределах жесткой границы. Если MV превышает связанное слишком много, ограничение жесткого шага может сделать исправление связанного нарушения в следующем интервале невозможным.

Если объект подвержен нарушениям порядка и существуют либо жесткие ограничения выхода, либо жесткие смешанные ограничения ввода-вывода, то недопустимость QP является отдельной возможностью.

Все Model Predictive Control Toolbox™ ограничения (кроме переменной slack nonnegativity) могут быть soft. Когда ограничение мягкое, контроллер может считать MV оптимальным, хотя и предсказывает нарушение этого ограничения. Если все выходы объекта, шаг MV и пользовательские ограничения являются мягкими (так как они по умолчанию), недопустимость QP не возникает. Однако эффективность контроллера может быть некачественной.

Чтобы смягчить ограничение, задайте соответствующее равное значение проблемы релаксации (ECR) положительное значение (нуль подразумевает жесткое ограничение). Чем больше значение ECR, тем больше вероятность того, что контроллер сочтет оптимальным нарушение ограничения в порядок удовлетворения другой вашей эффективности целей. Программное обеспечение Model Predictive Control Toolbox обеспечивает значения ECR по умолчанию, но, что касается весов функции затрат, вам может потребоваться настроить значения ECR в порядок, чтобы достичь приемлемой эффективности.

Чтобы понять, как работает смягчение ограничений, предположим, что ваша функция затрат использует $w_{i, j}^{u} = w_{i, j}^{Δ u} = 0$ , придавая как инкременты MV, так и MV нулевой вес в функции затрат. Только выход отслеживания уставки и условия нарушения ограничений ненулевые. В этом случае функция затрат:

$J (z_{k}) = \sum_{j = 1}^{n_{y}} \sum_{i = 1}^{p} {\frac{w_{i, j}^{y}}{s_{j}^{y}} [r_{j} (k + i | k) - y_{j} (k + i | k)]}^{2} + ρ_{ε} ε_{k}^{2} .$

Предположим, что вы также задали жесткие границы MV с $V_{j, m i n}^{u} (i) = 0$ и $V_{j, m a x}^{u} (i) = 0$ . Затем эти ограничения упрощают:

$\frac{u_{j, m i n} (i)}{s_{j}^{u}} \leq \frac{u_{j} (k + i - 1 | k)}{s_{j}^{u}} \leq \frac{u_{j, m a x} (i)}{s_{j}^{u}}, i = 1 : p, j = 1 : n_{u} .$

Таким образом, переменная slack, _εk, больше не появляется в вышеприведенных уравнениях. Вы также задали мягкие ограничения на выходы объекта с $V_{j, m i n}^{y} (i) > 0$ и $V_{j, m a x}^{y} (i) > 0$ .

$\frac{y_{j, m i n} (i)}{s_{j}^{y}} - ε_{k} V_{j, m i n}^{y} (i) \leq \frac{y_{j} (k + i | k)}{s_{j}^{y}} \leq \frac{y_{j, m a x} (i)}{s_{j}^{y}} + ε_{k} V_{j, m a x}^{y} (i), i = 1 : p, j = 1 : n_{y} .$

Теперь предположим, что нарушение порядка выдвинуло выход объекта выше заданной верхней границы, но QP с жесткими выходными ограничениями будет допустимым, то есть в решении QP можно избежать всех нарушений ограничений. QP предполагает компромисс между выходом отслеживания уставки и нарушением ограничений. Переменная slack, _εk, должна быть неотрицательной. Его внешний вид в функции затрат препятствует, но не препятствует, оптимальному _εk > 0. Однако больший _ρε вес увеличивает вероятность того, что оптимальное _εk будет маленьким или нулевым.

Если оптимальное _εk > 0, по крайней мере, одно из связанных неравенств должно быть активным (при равенстве). Относительно большой $V_{j, m a x}^{y} (i)$ облегчает удовлетворение ограничения с помощью небольшого _εk. В этом случае,

$\frac{y_{j} (k + i | k)}{s_{j}^{y}}$

может быть больше, не превышая

$\frac{y_{j, m a x} (i)}{s_{j}^{y}} + ε_{k} V_{j, m a x}^{y} (i) .$

Заметьте, что $V_{j, m a x}^{y} (i)$ не устанавливает верхний предел для нарушения ограничений. Скорее это коэффициент настройки, определяющий, легко ли или трудно удовлетворить мягкое ограничение.

Совет

Использование безразмерных переменных упрощает настройку ограничений. Определите соответствующие масштабные коэффициенты для каждой входной и выходной переменной объекта. См. «Задание масштабных коэффициентов».
Чтобы указать относительную величину допустимого нарушения, используйте параметр ECR, сопоставленный с каждым ограничением. Основные принципы заключаются в следующем:
- 0 - Нарушение не разрешено (жесткое ограничение)
- 0.05 - Допускается очень маленькое нарушение (почти жесткое)
- 0.2 - Допускается небольшое нарушение (довольно жесткое)
- 1 - средняя мягкость
- 5 - допускается нарушение, превышающее среднее (довольно мягкое)
- 20 - допускается крупное нарушение (очень мягкое)
Используйте параметр смягчения полного ограничения контроллера (свойство объекта контроллера: Weights.ECR) для наказания допустимого нарушения мягких ограничений относительно других условий функции затрат. Установите Weights.ECR свойство таким образом, что соответствующий штраф на 1-2 порядка величины больше, чем типичная сумма трех других членов функции затрат. Если нарушения ограничений кажутся слишком большими во время тестов симуляции, попробуйте увеличить Weights.ECR в разы 2-5.
Однако имейте в виду, что чрезмерно большое Weights.ECR искажает оптимизацию СН, приводя к неподходящим настройкам СН, когда имеют место нарушения ограничений. Чтобы проверить это, отобразите значение функции затрат во время симуляций. Если его величина увеличений более чем на 2 порядка величины, когда происходит нарушение ограничений, рассмотрите уменьшение Weights.ECR.
Нарушения порядка и ошибки предсказания могут привести к неожиданным нарушениям ограничений в реальной системе. Попытка предотвратить эти нарушения путем усложнения ограничений часто снижает эффективность контроллера.

См. также

review

Документация