Рассмотрите многопараметрическую систему управления с обратной связью, показанную на следующем рисунке. В порядок к количественной оценке многомерных полей устойчивости и эффективности таких систем можно использовать сингулярные значения матриц передаточной функции с обратной связью от r до каждого из трех выходов e, u и y, viz.
где L (s) является матрицей цикла передаточной функции
| (1) |
Блок схема многопараметрической системы управления с обратной связью
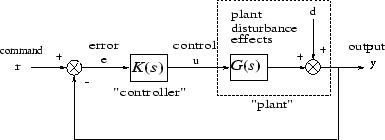
Две матрицы S (s) и T (s) известны как функция чувствительности и дополнительная функция чувствительности, соответственно. Матричный R (s) не имеет общего имени. Сингулярные графики Бода каждой из трех матриц передаточной функции S (s), R (s) и T (s) играют важную роль в разработке устойчивой многомерной системы управления. Сингулярные значения матрицы цикла передаточной функции L (s) важны, потому что L (s) определяет матрицы S (s) и T (s).
Сингулярные значения S (j ω) определяют ослабление нарушения порядка, потому что S (<reservedrangesplaceholder2>) является на самом деле передаточной функцией с обратной связью от нарушения порядка d к y выхода объекта - см. Блок-схему Многовариантной Системы Управления с обратной связью. Таким образом, спецификация эффективности ослабления нарушения порядка может быть записана как
| (2) |
где - желаемый коэффициент ослабления нарушения порядка. Разрешение зависимость от частоты ω позволяет вам задать другой коэффициент ослабления для каждого частотного ω.
Диаграммы Боде сингулярного значения R (<reservedrangesplaceholder4>) и T (<reservedrangesplaceholder2>) используются, чтобы измерить запасы устойчивости многовариантных проектов обратной связи перед лицом совокупных волнений объекта ΔA и мультипликативных волнений объекта ΔM, соответственно. См. следующий рисунок.
Рассмотрим, как сингулярное значение диаграмма Боде дополнительной чувствительности T (s) определяет запас устойчивости для мультипликативных возмущений ΔM. Мультипликативный запас устойчивости по определению является «размером» наименьшего стабильного ΔM (s), который дестабилизирует систему на рисунке ниже, когда ΔA = 0.
Аддитивная/мультипликативная неопределенность
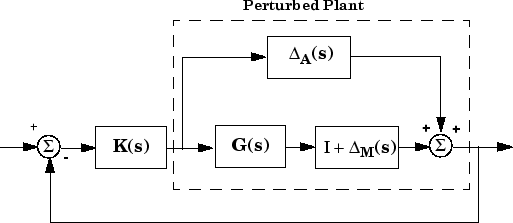
Взятие чтобы быть определением «размера» ΔM (jω), у вас есть следующая полезная характеристика «мультипликативной» устойчивости робастности:
Мультипликативная робастность:
Размер наименьшей дестабилизирующей мультипликативной ΔM неопределенности (s):
Чем меньше, тем чем больше будет размер наименьшего дестабилизирующего мультипликативного возмущения, и, следовательно, тем больше будет запас устойчивости.
Аналогичный результат доступен для связи запаса устойчивости перед лицом возмущений аддитивного объекта ΔA (s) с R (s), если вы принимаете быть определением «размера» ΔA (jω) на частоте
Аддитивная робастность:
Размер наименьшей ΔA дестабилизирующей аддитивной неопределенности:
Как следствие теорем робастности 1 и 2, обычно задают запасы устойчивости систем управления через неравенства сингулярных значений, такие как
| (3) |
| (4) |
где | <reservedrangesplaceholder3> 2 (<reservedrangesplaceholder2>) | и | <reservedrangesplaceholder1> 3 (<reservedrangesplaceholder0>) | соответствующие размеры самых больших ожидаемых совокупных и мультипликативных волнений объекта.
Распространенной практикой является объединение эффектов всей неопределенности объекта в одну фиктивную мультипликативную ΔM возмущения, чтобы можно было написать требования к системе управления
как показано Сингулярное значение Спецификаций на L, S и T.
Интересно отметить, что в верхней половине рисунка (выше линии 0 дБ),
в то время как в нижней половине спецификаций сингулярного значения на L, S и T (ниже линии 0 дБ),
Это происходит из-за того, что
если , и
если .

Спецификации сингулярных значений для L, S и T
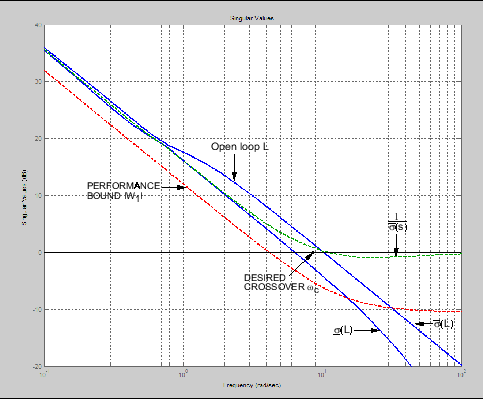
Таким образом, часто встречаются спецификации на нарушения порядка ослабления и мультипликативного запаса устойчивости, выраженные непосредственно в терминах запрещенных областей для Диаграмм Боде σi (L (jω)), как требования к формированию цикла сингулярных значений, либо как заданные верхние/нижние границы, либо как целевая требуемая форма цикла - см. предыдущий рисунок.
Для тех, кому более удобны классические концепции с одним циклом, существуют важные связи между мультипликативными запасами устойчивости, предсказанными и предсказанные классическими M-кругами, как найдено на графике Николса. Действительно, в случае с одним входом/одним выходом,
это именно та величина, которую вы получаете из M-кругов графика Николса. Таким образом, является мультицикл обобщением резонансного пика с обратной связью величины который, как узнают специалисты по классическому управлению, тесно связан с коэффициентом затухания доминирующих полюсов с обратной связью. Также оказывается, что можно связать , к классическим запасам по амплитуде GM и запасам по фазе, θM в каждом цикле обратной связи многопараметрической системы обратной связи Блока Диаграммы Системы управления по многопараметрической обратной связи через формулы:
(См. [6].) Эти формулы действительны и больше 1, как это обычно бывает. Поля применяются, даже когда возмущения усиления или фазы возмущения происходят одновременно в нескольких каналах обратной связи.
Нормы по бесконечности S и T также дают допуски на уменьшение усиления. Допуск на уменьшение усиления gm определяется как минимальная величина, на которую усиления в каждом цикле должны быть уменьшены в порядок дестабилизации системы. Верхние границы gm следующие:
Команда loopsyn позволяет вам спроектировать стабилизирующий контроллер обратной связи, чтобы оптимально сформировать частотную характеристику разомкнутого контура системы управления обратной связью MIMO, чтобы максимально точно соответствовать желаемой форме цикла Gd. Основной синтаксис loopsyn команда синтеза контроллера формирования контура является:
K = loopsyn(G,Gd)
Вот G - матрица передаточной функции LTI модели объекта управления MIMO, Gd - целевая необходимая форма цикла для передаточной функции цикла L=G*K, и K является оптимальным контроллером формирования контура. Контроллер LTI K имеет свойство, которое оно формирует цикл L=G*K так, чтобы она совпадала с частотной характеристикой Gd максимально близко, при условии ограничения, что компенсатор должен стабилизировать модель объекта управления G.