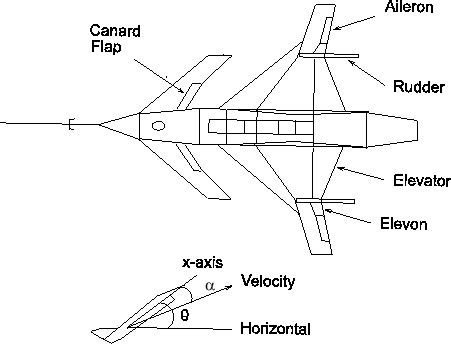
Чтобы увидеть, как loopsyn команда работает на практике, чтобы решить проблемы робастности и эффективности, снова рассмотрим модель самолета НАСА HiMAT, взятую из статьи Сафонова, Лауба и Хартманна [8]. Продольная динамика самолета HiMAT, обрезанная на 25000 ft и 0,9 Mach, нестабильны и имеют два право-полуплоскных фугоидных режима. Линейная модель имеет G реализации в пространстве состояний (s ) = C ( Is - A)–1B с шестью состояниями, с первыми четырьмя состояниями, представляющими угол атаки (α) и угол ориентации (θ) и их скорости изменения, и последними двумя, представляющими динамику привода управления высоты и полки - см. «Строение самолета» и «Геометрия вертикальной плоскости».
ag = [
-2.2567e-02 -3.6617e+01 -1.8897e+01 -3.2090e+01 3.2509e+00 -7.6257e-01;
9.2572e-05 -1.8997e+00 9.8312e-01 -7.2562e-04 -1.7080e-01 -4.9652e-03;
1.2338e-02 1.1720e+01 -2.6316e+00 8.7582e-04 -3.1604e+01 2.2396e+01;
0 0 1.0000e+00 0 0 0;
0 0 0 0 -3.0000e+01 0;
0 0 0 0 0 -3.0000e+01];
bg = [0 0;
0 0;
0 0;
0 0;
30 0;
0 30];
cg = [0 1 0 0 0 0;
0 0 0 1 0 0];
dg = [0 0;
0 0];
G = ss(ag,bg,cg,dg);Переменные управления - это приводы лифта и каната ( Выходными переменными являются угол атаки (α) и угол ориентации (
Строение самолета и геометрия вертикальной плоскости
Эта модель хороша на частотах ниже 100 рад/с с менее чем 30% изменением между истинным самолетом и моделью в этой частотной области значений. Однако, как отмечается в [8], он не обеспечивает надежного захвата поведения с очень высокой частотой, поскольку был получен путем обработки самолета как твёрдого тела и пренебрежения легкодемпфюзеляжными режимами изгиба фюзеляжа, которые происходят где-то между 100 и 300 рад/с. Эти немодулированные режимы изгиба могут вызвать отклонение до 20 дБ (то есть 1000%) между частотной характеристикой модели и фактическим летательным аппаратом для частоты Другие эффекты, такие как задержки привода управления и искривление топлива, также способствуют неточности модели на даже более высоких частотах, но доминирующие немоделированные эффекты являются режимами изгиба фюзеляжа. Можно думать об этих немодулированных режимах изгиба как о мультипликативной неопределенности размера 20 дБ и спроектировать свой контроллер с помощью loopsyn, убедившись, что цикл имеет коэффициент усиления менее -20 дБ на, и за его пределами, частоте, и даже 100 рад/с.
Спецификации проекта сингулярного значения
Спецификация робастности: Скат отката -20 дБ/десятилетие и коэффициент усиления цикла -20 дБ при 100 рад/с
Эффективность.: Минимизируйте функцию чувствительности как можно больше.
Обе характеристики могут быть учтены путем принятия в качестве желаемой формы цикла
<reservedrangesplaceholder3> <reservedrangesplaceholder2> (<reservedrangesplaceholder1>) =8 / s
s = zpk('s'); % Laplace variable s Gd = 8/s; % desired loop shape % Compute the optimal loop shaping controller K [K,CL,GAM] = loopsyn(G,Gd); % Compute the loop L, sensitivity S and complementary sensitivity T: L = G*K; I = eye(size(L)); S = feedback(I,L); % S=inv(I+L); T = I-S; % Plot the results: % step response plots step(T);title('\alpha and \theta command step responses');

% frequency response plots figure; sigma(L,'r--',Gd,'k-.',Gd/GAM,'k:',Gd*GAM,'k:',{.1,100}) legend('\sigma(L) loopshape',... '\sigma(Gd) desired loop',... '\sigma(Gd) \pm GAM, dB');

figure; sigma(T,I+L,'r--',{.1,100}) legend('\sigma(T) robustness','1/\sigma(S) performance')

Номер ± GAM, дБ (т.е. 20log10 (GAM)) сообщает вам точность, с которой вашloopsyn Система управления соответствует целевому циклу: