Вычисление сингулярных значений Ханкеля для стабильной/нестабильной или непрерывной/дискретной системы
[sv_stab,sv_unstab] = hankelsv(G,ErrorType,style)
hankelsv(G)
hankelsv(G,ErrorType,style)
[sv_stab,sv_unstab] = hankelsv(G,ErrorType,style) возвращает вектор-столбец SV_STAB содержащие сингулярные значения Ханкеля стабильной части G и SV_UNSTAB противостойкой части (если она существует). Hankel SV антистабельной части ss(a,b,c,d) вычисляется внутренне через ss(-a,-b,c,d). Дискретная модель преобразуется в непрерывную посредством билинейного преобразования.
hankelsv(G) без выходных аргументов рисует гистограмму сингулярных значений Ханкеля, таких как следующее:
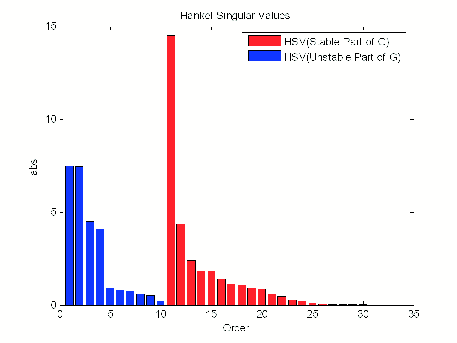
Чтобы сгенерировать штриховой график с заданным типом ошибки и стилем, используйте hankelsv(G,ErrorType,style). Эта таблица описывает необязательные входные параметры для hankelsvd.
Аргумент | Значение | Описание |
|---|---|---|
ERRORTYPE |
| Регулярные Hankel SV of G Hankel SV фазы матрицы Hankel SV общих факторов |
STYLE |
| Абсолютное значение шкала логарифма |
Если ErrorType = 'add', затем hankelsv реализует численно устойчивый метод квадратного корня для вычисления сингулярных значений Ханкеля [1]. Его алгоритм идет следующим образом:
Учитывая стабильную модель G, с грамматиками управляемости и наблюдаемости P и Q, вычислите SVD P и Q:
[Up,Sp,Vp] = svd(P); [Uq,Sq,Vq] = svd(Q);
Затем образуйте квадратные корни граммиан:
Lr = Up*diag(sqrt(diag(Sp))); Lo = Uq*diag(sqrt(diag(Sq)));
Сингулярные значения Ханкеля являются просто:
<reservedrangesplaceholder1> <reservedrangesplaceholder0>
Этот метод использует преимущества робастного алгоритма SVD и обеспечивает соответствие расчетов квадратному корню точности машины.
Если ErrorType = 'mult', затем hankelsv вычисляет сингулярное значение Ханкеля матрицы фаз G [2].
Если ErrorType = 'ncf', затем hankelsv вычисляет сингулярное значение Ханкеля нормированной пары простых множителей модели [3].
[1] Safonov, M.G., and R.Y. Chiang, «A Schur Method for Balanced Model Reduction», IEEE Trans. on Automat. Контр., т. AC-2, № 7, июль 1989, с. 729-733.
[2] Safonov, M.G., and R.Y. Chiang, «Снижение сложности модели for Robust Control: A Schur Относительной погрешности Method», International J. of Adaptive Control and Signal Processing, Vol. 2, pp. 259-272, 1988.
[3] Vidyasagar, M., Control System System Synthesis - Подход факторизации. Лондон: The MIT Press, 1985.